- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2016PUPC普林斯顿大学物理竞赛Onsite真题与答案免费下载
历年PUPC普林斯顿大学物理学术活动真题与答案免费下载
Onsite现场学术活动部分
翰林国际教育全网首发
力争超快速发布最全资料
为你
千千万万遍
2016PUPC普林斯顿大学物理学术活动完整版真题免费下载
Onsite现场学术活动部分此卷共3题
但每题下分不同数量的小题
完整版下载链接见文末
真题预览:
Problem 1. A Jelly-Filled Universe (10 points total)
Suppose the Universe is filled with some strange gelatinous substance which produces a pseudo-drag force. A particle of mass m will experience a braking force (which we will also call the pseudo-drag force)
F = - ka
where k is some positive constant and a is the particle’s acceleration. For the following questions, assume the particle moves in one dimension for simplicity.
a) (1 point) Suppose there are no other forces on the particle. Describe the motion of the particle’s position x(t) for all times t≥0, assuming its initial speed v(0) = v0 and initial position x(0) = x0.
b) (1 point) Now suppose the particle experiences a constant external force Fext > 0 beginning at t = 0. Describe the motion of the particle’s position x(t) for all times t≥0, assuming its initial speed v(0) = v0 and initial position x(0) = x0.
c) (1 point) What is the total work W done on the particle during the time interval 0 ≤t≤T under this constant applied force? (Include the work done by the applied force and the pseudo-drag force.)
d) (2 points) Describe the physical implication of the pseudo-drag force F for the particle. In particular, describe how this pseudo-drag force di↵ers from kinetic friction (a constant braking force) and low-velocity viscous drag (a braking force proportional to the particle’s speed). Please be as specific as possible in your explanation.
e) (1 point) Suppose the particle is dropped near the Earth’s surface where there is a gravitational field strength g. How long does it take (![]() t) for the particle to fall through a height h? (Assume the force of gravity is mg downward, and does not depend appreciably on the height of the particle above the surface of the Earth.)
t) for the particle to fall through a height h? (Assume the force of gravity is mg downward, and does not depend appreciably on the height of the particle above the surface of the Earth.)
f) (2 points) It is possible to recover the same result as in part e) for the movement of the particle by removing the pseudo-drag force F and replacing g with an e↵ective gravitational field ge↵.Find this effective field for a given value of k and m. Consider the limits in which m→0 and m→∞. Do your answers make sense? Explain.
g) (2 points) In electromagnetism, the Abraham-Lorentz force is a braking force that depends on the derivative of the particle’s acceleration:
![]()
where q is some constant and m is the particle’s mass, included for convenience. Including a time-varying external force Fext(t), the equation of motion is
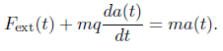
We can integrate this expression to find the solution for a(t),
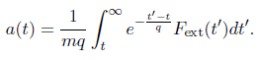
Suppose a constant external force Fext(t)= Fext is turned on at some faraway time t = T> 0 and lasts for all t≥T . What is the acceleration a(t) of the particle for t≥0 according to the solution for a(t) given above? What is strange about this situation? Please be specific by commenting on any times of interest.
完整版真题下载链接请注册或登录后查看
文件为PDF格式
推荐使用电脑下载
2016PUPC普林斯顿大学物理学术活动完整版答案免费下载
请点击访问下方链接进入下载页面
免费领取最新年份学术活动真题及解析

翰林学员全站资料免费打包下载,专享高速下载通道。
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





