- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2016PUPC普林斯顿大学物理竞赛Onsite答案免费下载
历年PUPC普林斯顿大学物理学术活动真题与答案免费下载
Onsite现场学术活动部分
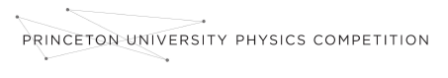
翰林国际教育全网首发
力争超快速发布最全资料
为你
千千万万遍
部分真题答案预览:
Problem 1. A Jelly-Filled Universe (10 points total)
a) With no other external forces on the particle, a = 0. We can show this using Newton’s second law:
- ka = ma,
which yields a = 0. Therefore,
x = x0 + v0t.
b) Again, using Newton’s laws we have F - ka = ma, which yields a = F/(k + m). We see that the pseudo-drag force acts by contributing an effective mass to the particle. Integrating, we get
![]()
so
![]()
c) We know that the net force on the particle is constant. Defining the acceleration a0 = F/(k + m) from part b, we find
![]()
The net work done is therefore the change in kinetic energy during the time T :
![]()
d)Kinetic friction is a constant braking force, so in a given time interval ![]() t the particle experiences a decrease in speed of
t the particle experiences a decrease in speed of![]() v α-
v α-![]() t. That is, the speed decreases at a constant rate. For viscous drag, the force increases linearly with speed, so
t. That is, the speed decreases at a constant rate. For viscous drag, the force increases linearly with speed, so![]() v α-v
v α-v![]() t, which implies that the speed decreases exponentially fast v∼exp( -kt). Unlike the other forces, the pseudo-drag force only acts in the presence of other forces. Alone, it has no effect on the system. In the presence of other forces, it acts by increasing the effective mass of the particle to m →m + k.
t, which implies that the speed decreases exponentially fast v∼exp( -kt). Unlike the other forces, the pseudo-drag force only acts in the presence of other forces. Alone, it has no effect on the system. In the presence of other forces, it acts by increasing the effective mass of the particle to m →m + k.
e)The force of gravity is Fg = −mg, where m is the particle’s gravitational mass. Using Newton’s second law, we find
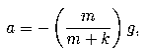
so the integrated equations give
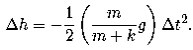
Solving for the time elapsed, we find
f) It is indeed possible to replace g with an e↵ective gravitational field ge↵. Studying Newton’s second law, we see that
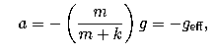
which implies that we should set
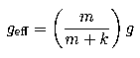
Taking the limits, we get
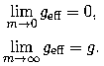
These results make sense. As m→0, the particle becomes massless, so it is no longer affected by gravity. So, it doesn’t matter whether there is a gravitational field (g ≠ 0) or not (geff= 0). In the second case, we have that the particle is infinitely massive. We no longer expect the the pseudo-force, which contributes a constant, finite term k to the effective mass, to matter. Thus, we expect geff= g, since the pseudo-drag force no longer contributes.
完整版真题资料可以底部二维码免费领取↓↓↓
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





