AMC10/12 A卷完美收官!
最新考试真题速来看!
翰林国际教育在得到试题的第一时间
就快马加鞭为同学们整理好了!
一起来看看此次新鲜出炉的真题吧!
翰林在官方允许试题解禁的第一时间
为大家宣布真题,答案及解析!
01AMC10 A卷考试真题
1.What is the value of (22−2)-(32−3)+(42−4)?
(A) 1 (B) 2 (C) 5 (D) 8 (E) 12
2. Portia’s high school has 3 times as many students as Lara’s high school. The two high schools have a total of 2600 students. How many students does Portia’s high school have?
(A) 600 (B) 650 (C) 1950 (D) 2000 (E) 2050
3.The sum of two natural numbers is 17,402. One of the two numbers is divisible by 10. If the units digit of that number is erased, the other number is obtained. What is the difference of these two numbers?
(A) 10,272 (B) 11,700 (C) 13,362 (D) 14,238 (E) 15,426
4.A cart rolls down a hill, traveling 5 inches the first second and accelerating so that during each successive 1-second time interval, it travels 7 inches more than during the previous 1-second interval. The cart takes 30 seconds to reach the bottom of the hill. How far, in inches, does it travel?
(A) 215 (B) 360 (C) 2992 (D) 3195 (E) 3242
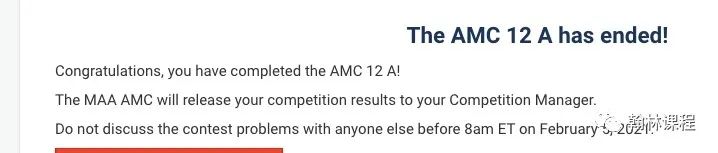
5.The quiz scores of a class with k>12 students have a mean of 8. The mean of a collection of 12 of these quiz scores is 14. What is the mean of the remaining quiz scores in terms of k?
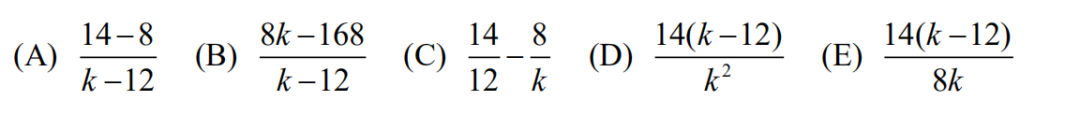
6.Chantal and Jean start hiking from a trailhead toward a fire tower. Jean is wearing a heavy backpack and walks slower. Chantal starts walking at 4 miles per hour. Halfway to the tower, the trail becomes really steep, and Chantal slows down to 2 miles per hour. After reaching the tower, she immediately turns around and descends the steep part of the trail at 3 miles per hour. She meets Jean at the halfway point. What was Jean’s average speed, in miles per hour, until they meet?
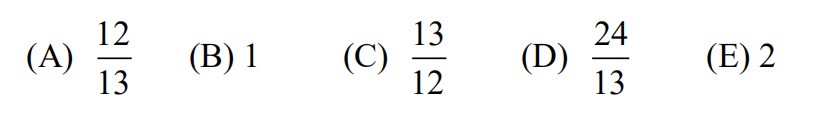
7. Tom has a collection of 13 snakes, 4 of which are purple and 5 of which are happy. He observes that
all of his happy snakes can add
none of his purple snakes can subtract, and
all of his snakes that can’t subtract also can’t add.
Which of these conclusions can be drawn about Tom’s snakes?
(A) Purple snakes can add.
(B) Purple snakes are happy.
(C) Snakes that can add are purple.
(D) Happy snakes are not purple.
(E) Happy snakes can’t subtract.
8.When a student multiplied the number 66 by the repeating decimal,
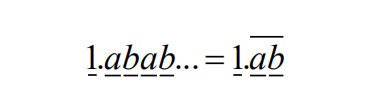 Where a and b are digits, he did not notice the notation and just multiplied 66 times
Where a and b are digits, he did not notice the notation and just multiplied 66 times
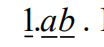 Later he found that his answer is 0.5 less than the correct answer. What is the 2- digit integer ab ?
Later he found that his answer is 0.5 less than the correct answer. What is the 2- digit integer ab ?
(A) 15 (B) 30 (C) 45 (D) 60 (E) 75
9.What is the least possible value of
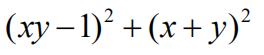 for real numbers x and y?
for real numbers x and y?
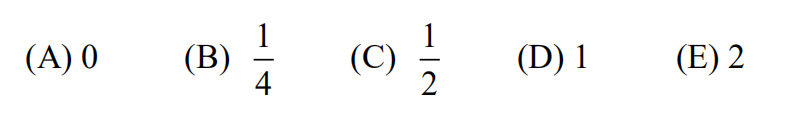 10.Which of the following is equivalent to
10.Which of the following is equivalent to
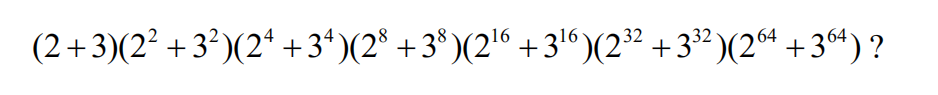
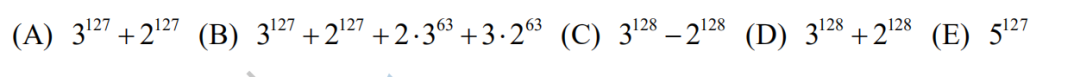 11.For which of the following integers b is the base-b number 2021b−221b not divisible by 3?
11.For which of the following integers b is the base-b number 2021b−221b not divisible by 3?
(A) 3 (B) 4 (C) 6 (D) 7 (E) 8
12.Two right circular cones with vertices facing down as shown in the figure below contain the same amount of liquid. The radii of the top of the liquid surfaces are 3cm and 6cm. Into each cone is dropped a spherical marble of radius 1cm, which sinks to the bottom and is completely submerged without spilling any liquid. What is the ratio of the rise of the liquid level in the narrow cone to the liquid level in the wide cone?
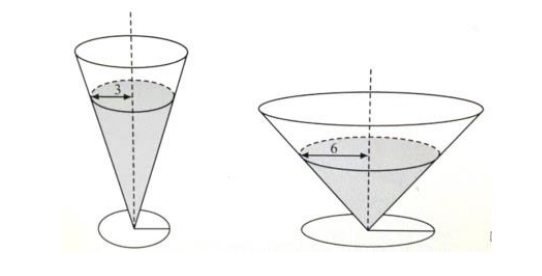
(A) 1:1 (B) 47:43 (C) 2:1 (D) 40:13 (E) 4:1
13.What is the volume of tetrahedron ABCD with edge lengths AB=2, AC=3, AD=4
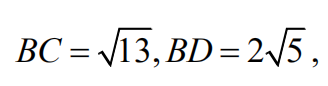 and CD=5?
and CD=5?
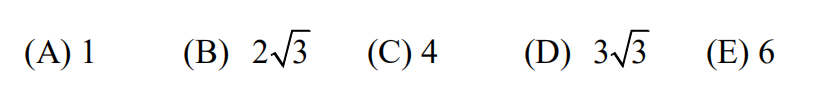 14.Ali the roots of polynomial
14.Ali the roots of polynomial
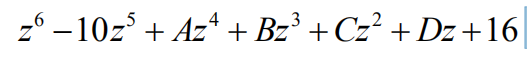 are positive integers, possibly repeated. What is the value of B?
are positive integers, possibly repeated. What is the value of B?
(A) -88 (B) -80 (C) -64 (D) -41 (E) -40
15.Values for A, B, C, and D are to be selected from {1, 2, 3, 4, 5, 6} without replacement (i.e., no two letters have the same value). How many ways are there to make such choices so that the two curves y = Ax2+B and y = Cx2+D intersect? (The order in which the curves are listed does not matter; for example, the choices A=3. B=2, C=4, D=1 is considered the same as the choices A = 4, B=1, C= 3. D=2.)
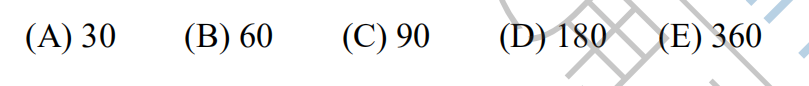 16.In the following list of numbers, the integer n appears n times in the list for 1≤n ≤200
16.In the following list of numbers, the integer n appears n times in the list for 1≤n ≤200
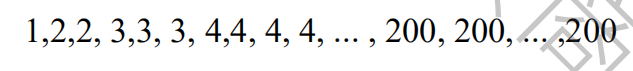 What is the median of the numbers in this list?
What is the median of the numbers in this list?
(A) 100.5 (B) 134 (C) 142 (D) 150.5 (E) 167
17.

(A) 65 (B) 132 (C) 157 (D) 194 (E) 215
18.

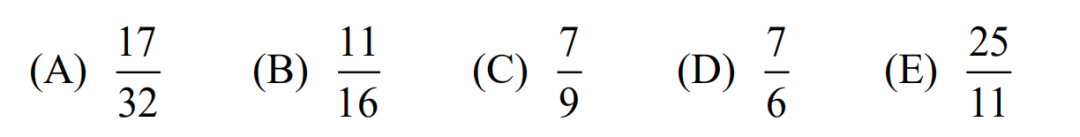 19.The area of the region bounded by the graph of
19.The area of the region bounded by the graph of
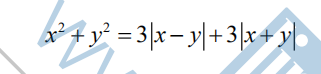 is m+nπ, where m and n are integers. What is m+n?
is m+nπ, where m and n are integers. What is m+n?
(A) 18 (B) 27 (C) 36 (D) 45 (E) 54
20.In how many ways can the sequence 1,2,3,4,5 be rearranged so that no three consecutive terms are increasing and no three consecutive terms are decreasing?
(A) 10 (B) 18 (C) 24 (D) 32 (E) 44
21.

(A) 47 (B) 52 (C) 55 (D) 58 (E) 63
22.Hiram's algebra notes are 50 pages long and are printed on 25 sheets of paper: the first sheet contains pages 1 and 2 the second sheet contains pages 3 and 4. and so on. One day he leaves his notes on the table before leaving for lunch. and his roommate decides to borrow some pages from the middle of the notes. When Hiram comes back, he discovers that his roommate has taken a consecutive set of sheets from the notes and that the average (mean) of the page numbers on all remaining sheets is exactly 19 How many sheets were borrowed?
(A) 10 (B) 13 (C) 15 (D) 17 (E) 20
23.Frieda the frog begins a sequence of hops on a 3×3 grid of squares, moving one square on each hop and choosing at random the direction of each hop up, down, left, or right. She does not hop diagonally. When the direction of a hop would take Frieda off the grid, she "wraps around" and jumps to the opposite edge. For example If Frieda begins in the center square and makes two hops "up”, the first hop would place her In the top row middle square, and the second hop would cause Frieda to Jump to the opposite edge, landing in the bottom row middle square. Suppose Frieda starts from the center square, makes at most four hops at random, and stops hopping If she lands on a comer square. What Is the probability that she reaches a corner square on one of the four hops?
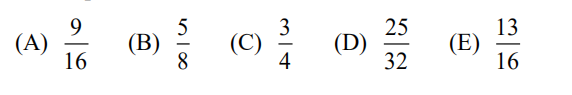 24.
24.

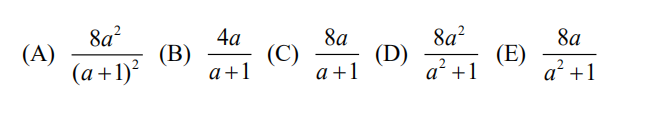 25.How many ways are there to place 3 Indistinguishable red chips, 3 indistinguishable blue chips, and 3 Indistinguishable green chips in the squares of a 3×3 grid so that no two chips of the same color are directly adjacent 10 each other, either vertically or horizontally?
25.How many ways are there to place 3 Indistinguishable red chips, 3 indistinguishable blue chips, and 3 Indistinguishable green chips in the squares of a 3×3 grid so that no two chips of the same color are directly adjacent 10 each other, either vertically or horizontally?
(A) 12 (B) 18 (C) 24 (D) 30 (E) 36
02AMC12 A卷考试真题
1.What is the value of
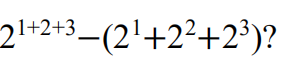
(A) 0 (B) 50 (C) 52 (D) 54 (E) 57
2.Under what conditions is
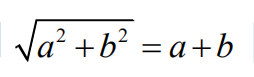 true, where a and b are real numbers?
true, where a and b are real numbers?
(A) It is never true
(B) It is true if and only if ab=0
(C) It is true if and only if a+b≥0
(D) It is true if and only if ab=0 and a+b≥0
(E) It is always true
3.The sum of two natural numbers is 17,402. One of the two numbers is divisible by 10. If the units digit of that number is erased, the other number is obtained. What is the difference of these two numbers?
(A) 10,272(B) 11,700 (C) 13,,362 (D) 14,238 (E) 15,426
4.Tom has a collection of 13 snakes, 4 of which are purple and 5 of which are happy. He observes that
all of his happy snakes can add
none of his purple snakes can subtract, and
all of his snakes that can’t subtract also can’t add
Which of these conclusions can be drawn about Tom’s snakes?
(A) Purple snakes can add.
(B) Purple snakes are happy.
(C) Snakes that can add are purple.
(D) Happy snakes are not purple.
(E) Happy snakes can’t subtract.
5.When a student multiplied the number 66 by the repeating decimal,
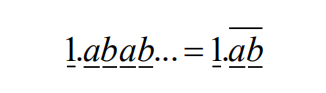 Where a and b are digits, he did not notice the notation and just multiplied 66 times 1.ab . Later he found that his answer is 0.5 less than the correct answer. What is the 2- digit integer ab ?
Where a and b are digits, he did not notice the notation and just multiplied 66 times 1.ab . Later he found that his answer is 0.5 less than the correct answer. What is the 2- digit integer ab ?
(A) 15 (B) 30 (C) 45 (D) 60 (E) 75
6.A deck of cards has only red cards and black cards. The probability of a randomly chosen card being red is 1/3. When 4 black cards are added to the deck, the probability of choosing red becomes 1/4 . How many cards were in the deck originally?
(A) 6 (B) 9 (C) 12 (D) 15 (E) 18
7.What is the least possible value of
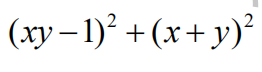 for real numbers x and y?
for real numbers x and y?
 8.A sequence of numbers is defined by D0 = 0, D1 = 0, D2 =1 and Dn= Dn-1 + Dn-3 for n≥3. What are the parities (evenness or oddness) of the triple of numbers (D2021, D2022, D2013), where E denotes even and 0 denotes odd
8.A sequence of numbers is defined by D0 = 0, D1 = 0, D2 =1 and Dn= Dn-1 + Dn-3 for n≥3. What are the parities (evenness or oddness) of the triple of numbers (D2021, D2022, D2013), where E denotes even and 0 denotes odd
(A) (O, E, O)
(B) (E, E, O)
(C) (E, O, E)
(D) (O, O, E)
(E) (O, O, O)
9.Which of the following is equivalent to
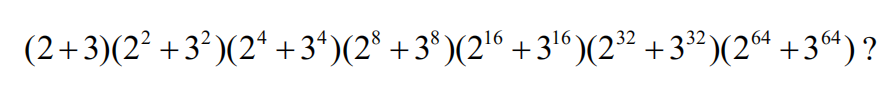
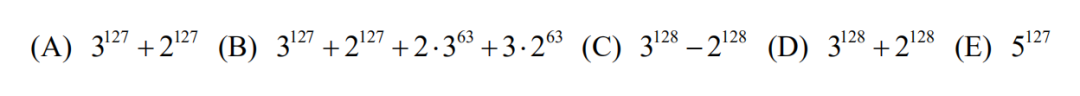 10.Two right circular cones with vertices facing down as shown in the figure below contain the same amount of liquid. The radii of the top of the liquid surfaces are 3cm and 6cm. Into each cone is dropped a spherical marble of radius 1cm, which sinks to the bottom and is completely submerged without spilling any liquid. What is the ratio of the rise of the liquid level in the narrow cone to the liquid level in the wide cone?
10.Two right circular cones with vertices facing down as shown in the figure below contain the same amount of liquid. The radii of the top of the liquid surfaces are 3cm and 6cm. Into each cone is dropped a spherical marble of radius 1cm, which sinks to the bottom and is completely submerged without spilling any liquid. What is the ratio of the rise of the liquid level in the narrow cone to the liquid level in the wide cone?
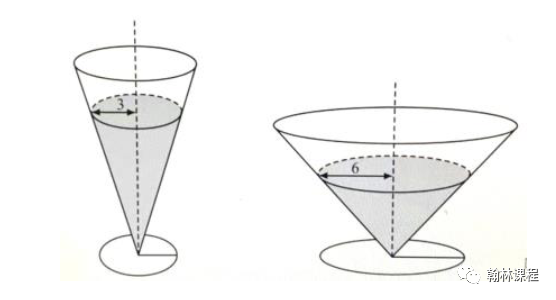
(A) 1:1 (B) 47:43 (C) 2:1 (D) 40:13 (E) 4:1
11.A laser is placed at the point (3, 5). The laser beam travels in a straight line. Larry wants the beam to hit and bounce off the y-axis, then hit and bounce off the x-axis, the hit the point (7, 5). What is the total distance the beam will travel along this path?
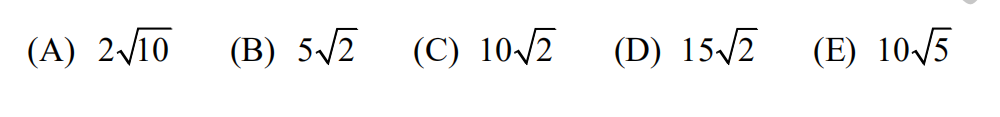 12.Ali the roots of polynomial are positive
12.Ali the roots of polynomial are positive
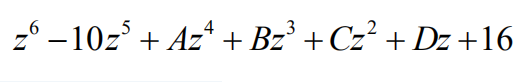 integers, possibly repeated. What is the value of B?
integers, possibly repeated. What is the value of B?
(A) -88 (B) -80 (C) -64 (D) -41 (E) -40
13.Of the following complex number z, which one has the property that z5 has the greatest real part?
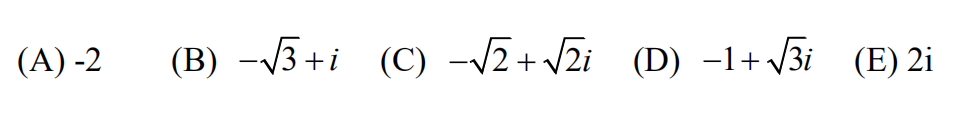 14.
14.
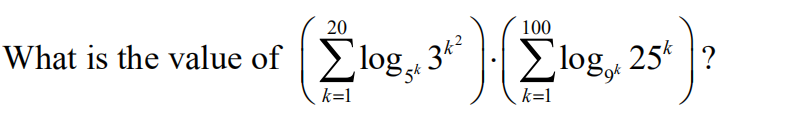
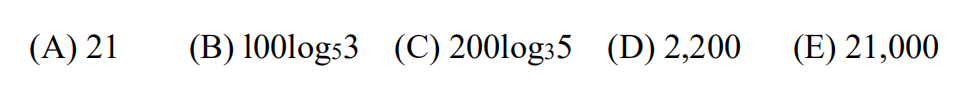
15.A choir director must select a group of singers from among his 6 tenors and 8 basses. The only requirements are that the difference between the numbers of tenors and basses must be a multiple of 4, and the group must have at least one singer. Let N be the number of groups that could be selected. What is the remainder when N is divided by 100?
(A) 47 (B) 48 (C) 83 (D) 95 (E) 9616.In the following list of numbers, the integer n appears n times in the list for 1≤n ≤200
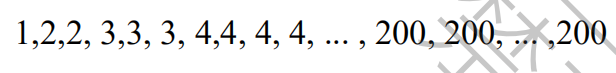 What is the median of the numbers in this list?
What is the median of the numbers in this list?
(A) 100.5 (B) 134 (C) 142 (D) 150.5 (E) 167
17.

(A) 65 (B) 132 (C) 157 (D) 194 (E) 215
18.

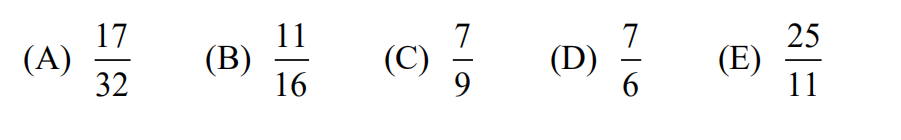 19.How many solutions does the equation sin
19.How many solutions does the equation sin
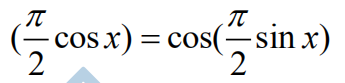 have in the closed interval [0,π ]
have in the closed interval [0,π ]
(A) 0 (B) 1 (C) 2 (D) 3 (E) 4
20.Suppose that on a parabola with vertex V and focus F there exists a point A such that AF=20 and AV=21. What is the sum of all possible values of the length FV?
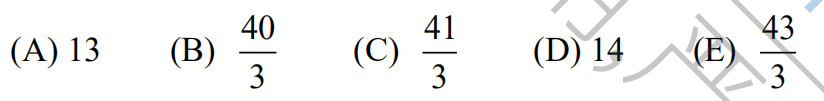 21.
21.

(A) 7 (B) 9 (C) 11 (D) 13 (E) 15
22.

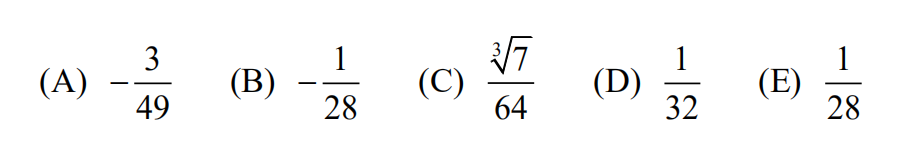
23.Frieda the frog begins a sequence of hops on a 3×3 grid of squares, moving one square on each hop and choosing at random the direction of each hop up, down, left, or right. She does not hop diagonally. When the direction of a hop would take Frieda off the grid, she "wraps around" and jumps to the opposite edge. For example If Frieda begins in the center square and makes two hops "up”, the first hop would place her In the top row middle square, and the second hop would cause Frieda to Jump to the opposite edge, landing in the bottom row middle square. Suppose Frieda starts from the center square, makes at most four hops at random, and stops hopping If she lands on a comer square. What Is the probability that she reaches a corner square on one of the four hops?
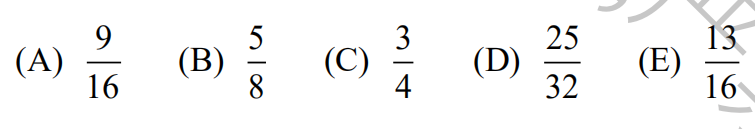 24.
24.

(A) 110 (B) 114 (C) 118 (D) 122 (E) 126
25.Let d(n) denote the number of positive integers that divide n, including 1 and n. For example, d(1)=1, d(2)=2, and d(12)=6. (This function is known as the divisor function.) Let
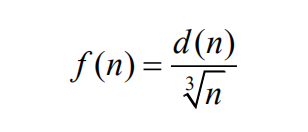
There is a unique positive integer N such that f(N)>f(n) for all positive integers n≠N. what is the sum of the digits of N?
(A) 5 (B) 6 (C) 7 (D) 8 (E) 9
以上就是刚刚结束的AMC10/12 A卷的全部真题了
小伙伴们都考的如何呢?
AMC10/12 B卷将2月11日准时开考
预祝各位考生旗开得胜,斩获佳绩!
想要获取AMC10/12 A卷真题的答案吗?
想要提前听名师的真题讲解视频吗?
扫描下方二维码,获取真题答案哦!
03 备战AMC,从现在开始!
AMC系列考试最具有含金量的爬藤学术活动!想要先人一步在AMC考试中考出好成绩吗?翰林金牌AMC课程助力你的大考!
数学学术活动类班课
| 班课名称 | 人数 | 班课时间 |
| AMC8基础班 | 3-8人 | 5.8~9.18 09:00~11:00 |
| AMC10刷题班 | 3-8人 | 2.6 上午10-12下午4-6
2.7下午1-3 2.8-2.10上午10-12下午4-6 |
| AMC10基础全程班 | 3-8人 | 3.6-7.3 每周六10:00-12:00 7.10-8.28 每周六9-12 |
| AMC10基础全程班 | 3-8人 | 3.6-7.17 每周六19:00-21:00 |
| AMC10基础全程班 | 3-8人 | 3.7-7.4 每周日10:00-12:00 7.11-8.29 每周日9:00-12:00 |
| AMC10基础全程班 | 3-8人 | 3.7-7.18 每周日14:00-17:00 |
| AMC10基础全程班 | 3-8人 | 3.7-7.18每周日上午8-11 |
| AMC10强化班 | 3-8人 | 4.18-8.29每周日9:00-11:00 |
| AMC10强化班 | 3-8人 | 4.11-8.22每周日19:00-21:00 |
| AMC12刷题班 | 3-8人 | 2.6-2.10 每天上午10-12 及 下午2:00-4 :00 |
| AMC12基础全程班 | 3-8人 | 2.21-9.12
每周日下午2:00~4:00 |
| AMC12基础全程班 | 3-8人 | 3.7-7.4 每周日10:00-12:00 7.11-8.29 每周日9-12 |
| AMC12基础全程班 | 3-8人 | 3.6-8.21 每周六19:00-22:00 |
| AMC12基础全程班 | 3-8人 | 3.6-7.3 每周六10:00-12:00 7.10-8.28 每周六9-12 |
| AMC12基础全程班 | 3-8人 | 3.13-7.10 每周六10:00-12:00 7.17-9.4 每周六9-12 |
| AMC12基础班 | 3-8人 | 4.10-8.21每周六19:00-22:00 |
| AMC12强化班 | 3-8人 | 3.13-7.17每周六14:00-16:00 |
| AMC12强化班 | 3-8人 | 4.10-8.21每周六19:00-21:00 |
| AMC12强化班 | 3-8人 | 4.11-8.22每周日14:00-16:00 |
| AMC12强化班 | 3-8人 | 4.10-8.21每周日19:00-21:00 |
| BmMT全程班 | 3-8人 | 1.9-3.6 每周六日13:00-15:00 (2.12,2.13休息) |
| BmMT全程班 | 3-8人 | 1.9-3.6 每周六日8:00-10:00 (2.12,2.13休息)
(最后一次课需要调整待定) |
| Mathleague第二阶段
(3-4年级) |
3-8人 | 2/1-2/19每周一到周五
上午9-11(2/10-2/16休息) |
| Mathleague第二阶段
(5-6年级) |
3-8人 | 2/1-2/19 每周一到周五下午2-4(2/10-2/16休息) |
| Mathleague第二阶段
(7-8年级) |
3-8人 | 2/1-2/19 每周一到周五晚上6-8(2/10-2/16休息) |
| 袋鼠3-4年级班 | 3-8人 | 1.16-3.21 每周六周日
14:00-16:00 |
| 袋鼠5-6年级班 | 3-8人 | 1.16-3.27 每周六周日16:30-18:30(1.17休息) |
数学学术活动战绩(2017-2020)
美国AMC系列
🏆2020翰林学员美国考团AIME晋级率93.3%,目前已统计到的参考学员AIME晋级率90.9%。来自全国各地的10位学员在AMC12B卷中获得了平均123分的好成绩,均分超过DHR!所有AMC12A+B联考学员均获得大幅度提分,平均提分39.75分。
🏆2019-2020赛季,AMC12B最高分132分,AMC12A最高分118.3分,AMC10B最高分133.5分,两位学员AIME分别以11分与12分晋级USAMO美国数学奥林匹克。
🏆2019翰林学员中1名AMC8满分,根据已有反馈:AMC10A美高学员均分123分,AMC10B学员均分124分,AMC12A美高学员均分108分,AMC10B学员均分111分;除部分未参赛学员,AMC10/12小班课学员综合AIME晋级率52/67,接近80%。
🏆2018翰林学员中2名AMC8满分,AMC10均分126,AMC12均分115,一对一学员AIME晋级率100%,AIME最高分12/15。
澳洲AMC
🏆2020澳洲AMC翰林学员中 A等级:一等奖2名,二等奖2名,三等奖2名。B等级:二等奖1名,三等奖2名。D等级:一等奖1名,二等奖1名。E等级:二等奖1名。
Euclid欧几里得数学学术活动
🏆2019欧几里得数学学术活动翰林学员,75-80分2人, 84-87分5人。
ARML系列
🏆2020ARML区域赛个人赛:1人华西赛区前20,1人华南赛区前100。
🏆2020ARML区域赛团队赛:5位学员获得团队铜奖,并晋级下一轮晋级挑战赛(power contest)(团队编号604)。
Math League数学大联盟
🏆2019Math League学术活动第一阶段:翰林学员一等奖12名,二等奖18名,三等奖13名,获奖率95%(参赛学生45位,43位获奖);第二阶段:18名学生全部晋级美国总决赛,晋级率100%。
🏆2020夏季挑战赛,翰林学员获得金奖6枚,银奖6枚,铜奖7枚,4名学员获得优胜奖。
BMT伯克利数学思维挑战
🏆2020BMT翰林学员在个人特长赛微积分比赛中获得全球唯一满分,个人特长赛代数比赛获得中国区前三,中国区团队二等奖,1名学员获得全国第三名。





