- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2004COMC加拿大数学公开赛真题答案免费下载
历年 Canadian Open Mathematics Challenge加拿大数学公开赛
真题与答案下载
翰林国际教育全网首发
力争超快速发布最全资料
助你在升学路上一帆风顺
为你
千千万万遍
2004 COMC真题答案免费下载
共计2.5小时考试时间
此套试卷由两部分题目组成
Part A共8题,每题5分
Part B共4题,每题10分
共计12题,满分80分
不可使用任何计算器
完整版下载链接见文末
部分真题预览:
Part A Solutions:
A6)Answer: 0 . Two Solutions:
- Solution 1: We can write down the elements of S: 357, 375, 537, 573, 735, 753.
The sum of these elements is 357 + 375 + 537 + 573 + 735 + 753 = 3330.
Since 3330 is divisible by 9 (because the sum of its digits is divisible by 9), the remainder when we divide by 9 is 0. - Solution 2: There are six numbers formed with the three given numbers.
Two of these numbers have a 3 in the 100s position, two have a 5 in the 100s position, and two have a 7 in the 100s position.
The same can be said about the distribution of numbers in the 10s and units positions.
Therefore, the sum of the six numbers is 2(3 + 5 + 7)(100) + 2(3 + 5 + 7)(10) + 2(3 + 5 + 7)(1) = 3330
The remainder is 0 when 3330 is divided by 9.
Part B Solutions:
B3)
- Two Solutions:
- Solution 1: We start by assuming that three line segments on the map do form a triangle, and show that this is in fact impossible.
Notice that if restaurants X and Y are joined by a line segment, then either X is the closest restaurant to Y or Y is the closest restaurant to X (or both).
Assume that A, B and C are the three points on the map connect by segments.

To begin, we focus on the segment joining A to B. Let’s assume that A is the closest restaurant to B. (It doesn’t matter which direction we assume here.) This means that C is not the closest restaurant to B, so BA < BC.
But B and C are connected and C is not the closest restaurant to B. Therefore, B is the closest restaurant to C, which means CB < CA.
But C and A are also connected and A is not the closest restaurant to C. Therefore, C is the closest restaurant to A, which means AC < AB.
But this means that BA < BC, BC < AC and AC < BA. This cannot be the case.
Therefore, it is impossible for three line segments to form a triangle. - Solution 2: We prove this by showing that constructing a triangle is impossible.
We start by considering two locations A and B and the line segment AB.
Since A and B are connected, we can assume without loss of generality that A is closest to B. (The case B closest to A involves interchanging A and B, and the case of A and B closest to each other is included in the case of A closest to B.)
If A is closest to B and we add a new location C which is connected to B, then B must be closest to C (since C can’t also be closest to B along with A).
If we join C to A, then either C is closest to A or A is closest to C.
But A can’t be closest to C since B is closest to C.
Therefore, we must have C closest to A.
But then AC is shorter than AB, along with AB being shorter than BC (since A is closest to B), which means that AC is shorter than BC or A is closer to C than B is, which isn’t
true. This is a contradiction.
Therefore, we can’t construct a triangle.
- Solution 1: We start by assuming that three line segments on the map do form a triangle, and show that this is in fact impossible.
- We start by assuming that one restaurant can be connected to six others and show that this is impossible. From this we can conclude that no restaurant can be connected to more than five other restaurants (for if it could be joined to 8 others, say, then we could consider six of them only and reach a contradiction).
Assume that restaurant A can be connected to restaurants B, C, D, E, F, and H, where these restaurants are listed in clockwise order of their line segments joining to A.
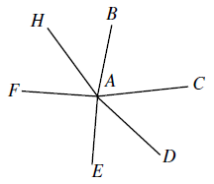
Consider restaurants A, B and C.
We know that B and C are both connected to A and both cannot be the closest neighbour to A. Thus, A must be the closest neighbour to one of these, say B. (It doesn’t matter which we choose).
Since A is the closest restaurant to B, then BA < BC.
Now consider the line joining C to A.
If C is the closest neighbour to A, then AC < AB, so AC < AB < BC.
If A is the closest neighbour to C, then CA < CB so CA < CB and BA < CB.
In either case, BC is the (strictly) longest side in 4ABC, and so must be opposite the (strictly) largest angle.
Since the angles in a triangle add to 180°, then if there is a largest angle, then this angle must be larger than 60°. Therefore, from the above reasoning, ∠BAC > 60°.
But we can reapply this reasoning to conclude that ∠CAD, ∠DAE,∠EAF, ∠FAH, and ∠HAB are each greater than 60°. But the sum of these six angles is 360°, since they will form a full circle around A, and six angles, each greater than 60°, cannot add to 360°. So we have a contradiction.
Therefore, it is impossible for a restaurant to be connected to more than five other restaurants.
完整版真题资料可以底部二维码免费领取↓↓↓
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





