- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
1999COMC加拿大数学公开赛真题免费下载
历年 Canadian Open Mathematics Challenge加拿大数学公开赛
真题与答案下载
翰林国际教育全网首发
力争超快速发布最全资料
助你在升学路上一帆风顺
为你
千千万万遍
1999 COMC真题免费下载
共计2.5小时考试时间
此套试卷由两部分题目组成
Part A共8题,每题5分
Part B共4题,每题10分
共计12题,满分80分
不可使用任何计算器
完整版下载链接见文末
部分真题预览:
Part A :
6)trapezoid, DEFG, is circumscribed about a circle that has centre C and radius 2, as is shown. The shorter of the two parallel sides, DE, has length 3 and angles DEF and EFG are right angles. Determine the area of the trapezoid.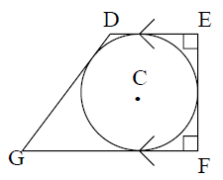
7)The sector OAB of a circle, with centre O, has a perimeter of 12. Determine the radius of the circle which maximizes the area of the sector.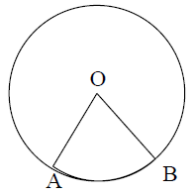
8)Find the smallest positive integer k so that the expression (14k+17)/(k-9) becomes a fraction in the form pd/qd where p, q and d are positive integers, p and q have no common divisors, and neither q nor d equals 1.
Part B :
1)
- Two identical triangles each have an area of 24. Their vertices are determined by the intersection of the lines with equations y = -4,x = 0 and y = (-3/4) x + b. Determine the two possible values for b.
- For either of the two given triangles, a circle can be drawn to pass through its three vertices. What is the radius of this circle?
完整版真题下载链接请注册或登录后查看
文件为PDF格式
推荐使用电脑下载
1999 COMC加拿大数学奥赛完整版答案免费下载
请持续关注,稍后更新
翰林学员全站资料免费打包下载,专享高速下载通道。
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





