历年 Canadian Open Mathematics Challenge加拿大数学公开赛

真题与答案下载

翰林国际教育全网首发

力争超快速发布最全资料

助你在升学路上一帆风顺

为你

千千万万遍

2009 COMC真题免费下载

共计2.5小时考试时间

此套试卷由两部分题目组成

Part A共8题，每题5分

Part B共4题，每题10分

共计12题，满分80分

不可使用任何计算器

完整版下载链接见文末

部分真题预览：

Part A :

3)Soroosh has 10 coins, each of which is either a quarter (worth 25 cents) or a dime (worth 10 cents). The total value of the dimes is greater than the total value of the quarters. What is the smallest possible number of dimes that he could have?

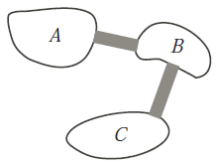
5)In the diagram, there are three islands labelled A, B and C. Islands A and B are joined by a bridge, as are islands B and C. Maya begins her journey on island A and travels between the islands by bridge only. She records the sequence of islands that she visits. She does not necessarily visit all three islands. If Maya makes 20 bridge crossings in total, how many possible sequences of islands A, B and C could she travel along?

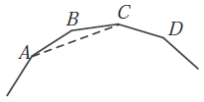
6)A polygon is called regular if all of its sides are equal in length and all of its interior angles are equal in size. In the diagram, a portion of a regular polygon is shown. If ∠ACD = 120°, how many sides does the polygon have?

Part B :

2)Triangle PQR has vertices P(7,13), Q(19,1) and R(1,1). Point M(4, 7) is the midpoint of PR; the midpoint of PQ is N.

1. Determine the equation of the median of the triangle that passes through points Q and M.
2. Determine the coordinates of G, the point of intersection of RN and QM.
3. Point F is on PR so that QF is perpendicular to PR. Point T is on PQ so that RT is perpendicular to PQ. Determine the coordinates of H, the point of intersection between altitudes QF and RT.
4. Determine which of G and H is closer to the origin.

完整版真题下载链接请注册或登录后查看

文件为PDF格式

推荐使用电脑下载

 

2009 COMC加拿大数学奥赛完整版答案免费下载

请持续关注，稍后更新

 

如需打包下载，请联系小助手了解更多

翰林学员全站资料免费打包下载，专享高速下载通道。