- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2010COMC加拿大数学公开赛真题免费下载
历年 Canadian Open Mathematics Challenge加拿大数学公开赛
真题与答案下载
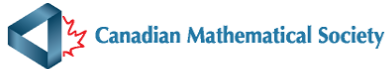
翰林国际教育全网首发
力争超快速发布最全资料
助你在升学路上一帆风顺
为你
千千万万遍
2010 COMC真题免费下载
共计2.5小时考试时间
此套试卷由两部分题目组成
Part A共8题,每题5分
Part B共4题,每题10分
共计12题,满分80分
不可使用任何计算器
完整版下载链接见文末
部分真题预览:
Part A :
3)In the diagram, each of the three circles has centre O. Diameter CD of the largest circle passes through points B, A and O. The lengths of the radii of the circles are OA = 2, OB = 4, and OC = 6. What is the area of the shaded region?
6)On a calculus exam, the average of those who studied was 90% and the average of those who did not study was 40%. If the average of the entire class was 85%, what percentage of the class did not study?
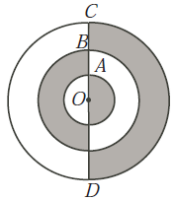
7)In the diagram, rectangle ABCD has AB = 20 and BC = 10. Points W and K are outside of the rectangle with WA = KC = 12 and WB = KD = 16. Determine the length of WK and express your answer in the form WK = m√n, where m and n are positive integers with m > 1.
Part B :
1)In each part of this problem, each of the variables in the grid is to be replaced with an integer. The sum of the integers in a row is given to the right of the row. The sum of the integers in a column is given at the bottom of the column. For example, from the grid to the right we can conclude that X+13 = 30, Y +11 = 23, X+Y = 29, and 13 + 11 = 24.
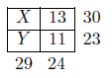
- Determine the value of C.
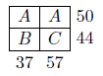
- Determine the value of n, the sum of the integers in the second column.
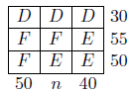
- Determine the value of P + Q.
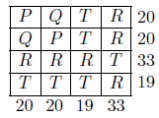
2)The parabola with equation y = x2 - 4x + 12 intersects the line with equation y = -2x + 20 at points A and B.
- Determine the coordinates of the points A and B.
- Determine the coordinates of the midpoint, M, of the segment AB.
- A line parallel to the line with equation y = -2x+20 intersects the parabola at distinct points P(p; p2 -4p+12) and Q(q; q2 -4q +12). Prove that p+q = 2.
- Point N is the midpoint of PQ. Explain why line segment MN is vertical.
完整版真题资料可以底部二维码免费领取↓↓↓
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





