- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2014PUPC普林斯顿大学物理竞赛Online真题与答案免费下载-Condensed Matter
历年PUPC普林斯顿大学物理学术活动真题与答案免费下载
Online线上学术活动部分
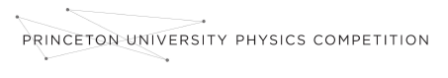
翰林国际教育全网首发
力争超快速发布最全资料
为你
千千万万遍
2014PUPC普林斯顿大学物理学术活动
Condensed Matter Online Part 完整版真题免费下载
Online线上学术活动部分此卷共9大题
但每题下分不同数量的小题
完整版下载链接见文末
真题预览:
If you choose to submit your solutions for the Condensed Matter part, you are NOT required to submit the Cosmology part!
This part will contain background material in crystal structure, quantum theory, resistivity and conductivity, superconductivity, the process underpinning the growing field of topological insulators, and, finally, Kondo insulators, a subtopic that is at the forefront of groundbreaking research in present day condensed matter physics.
Each section of the background material is followed by several conceptual and/or applied questions that you are expected to answer in any order you choose (but the material is structured in a way that would lead you through the assignment sequence logically).
Good luck!
Condensed matter physics deals with the study of systems made up of condensed phases of matter, and a great deal of research focuses on analyzing such systems on a micro-level. The behavior of these systems is explored using theories from solid state physics, quantum mechanics, electrodynamics, and statistical mechanics. In this part, you will explore some important concepts one encounters in condensed matter.
-
Crystal Structure background
Crystal lattices Condensed matter is largely concerned with the study of crystalline materials, or those with a regular, repeating structure. One reason is that crystals are easier to study than irregular matter. More importantly, most real solid materials are crystalline, including quartz, salt, and metals.
The structure of a crystal can be described in terms of a crystal lattice (or Bravais lattice), which specifies the periodic geometry in which the crystal units (e.g. atoms) are arranged. Two equivalent definitions of a Bravais lattice are:
- A Bravais lattice is an infinite array of discrete points with an arrangement and orientation that appears exactly the same, from whichever of the points the array is viewed
- A (three-dimensional) Bravais lattice consists of all points with position vectors R of the form:
![]() (1)
(1)
where the ni are integers.
The vectors ai, or primitive vectors, are said to span the lattice. Any point in the lattice can be reached from any other point by a sum of primitive vectors. It should be noted that the choice of primitive vectors is not unique; in fact, there are an infinite number of equivalent choices. A picture of a Bravais lattice with one choice of primitive vectors is provided in Figure 1.
A Bravais lattice is infinite by definition. Although real crystals are of course finite, they contain a very large number of points. The points in the center are so far from the surface that they are generally unaffected by the surface, so they behave as if in an infinite solid.
One important Bravais lattice, the body-centerd cubic (BCC) lattice, is shown in Figure 2. It can be formed by starting with a simple cubic lattice (whose points we call A) and adding a point in the center of
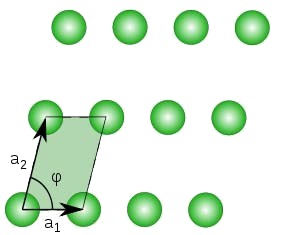
Figure 1: A 2D Bravais lattice with one set of possible primitive vectors shown.
Figure 2: A body-centered cubic (BCC) lattice.
each cube (which we call B). The B points may appear to be fundamentally different from the A points, but they are not. To see this, note that the B points can be connected to form cubes, where now the A points lie in the centers. Thus, each point has identical surroundings, satisfying definition 1 of a Bravais lattice.
This implies that the BCC lattice can be described by a set of primitive vectors. One choice is:
![]() (2)
(2)
A more symmetric choice is:
![]() (3)
(3)
In Problem 1.1, you will show that these choices are equivalent.
完整版真题资料可以底部二维码免费领取↓↓↓
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





