- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2015 AMC 8 真题与答案解析
2015 AMC 8 真题
答案解析请参考文末
Problem 1
How many square yards of carpet are required to cover a rectangular floor that is ![]() feet long and
feet long and ![]() feet wide? (There are
feet wide? (There are ![]() feet in a yard.)
feet in a yard.) ![]()
Problem 2
Point ![]() is the center of the regular octagon
is the center of the regular octagon ![]() , and
, and ![]() is the midpoint of the side
is the midpoint of the side ![]() What fraction of the area of the octagon is shaded?
What fraction of the area of the octagon is shaded? 
![]()
Problem 3
Jack and Jill are going swimming at a pool that is one mile from their house. They leave home simultaneously. Jill rides her bicycle to the pool at a constant speed of ![]() miles per hour. Jack walks to the pool at a constant speed of
miles per hour. Jack walks to the pool at a constant speed of ![]() miles per hour. How many minutes before Jack does Jill arrive?
miles per hour. How many minutes before Jack does Jill arrive? ![]()
Problem 4
The Centerville Middle School chess team consists of two boys and three girls. A photographer wants to take a picture of the team to appear in the local newspaper. She decides to have them sit in a row with a boy at each end and the three girls in the middle. How many such arrangements are possible? ![]()
Problem 5
Billy's basketball team scored the following points over the course of the first ![]() games of the season:
games of the season: ![]() If his team scores 40 in the 12th game, which of the following statistics will show an increase?
If his team scores 40 in the 12th game, which of the following statistics will show an increase? ![]()
Problem 6
In ![]() ,
, ![]() , and
, and ![]() . What is the area of
. What is the area of ![]() ?
? ![]()
Problem 7
Each of two boxes contains three chips numbered ![]() ,
, ![]() ,
, ![]() . A chip is drawn randomly from each box and the numbers on the two chips are multiplied. What is the probability that their product is even?
. A chip is drawn randomly from each box and the numbers on the two chips are multiplied. What is the probability that their product is even? ![]()
Problem 8
What is the smallest whole number larger than the perimeter of any triangle with a side of length ![]() and a side of length
and a side of length ![]() ?
? ![]()
Problem 9
On her first day of work, Janabel sold one widget. On day two, she sold three widgets. On day three, she sold five widgets, and on each succeeding day, she sold two more widgets than she had sold on the previous day. How many widgets in total had Janabel sold after working ![]() days?
days? ![]()
Problem 10
How many integers between ![]() and
and ![]() have four distinct digits?
have four distinct digits? ![]()
Problem 11
In the small country of Mathland, all automobile license plates have four symbols. The first must be a vowel (![]() or
or ![]() ), the second and third must be two different letters among the
), the second and third must be two different letters among the ![]() non-vowels, and the fourth must be a digit (
non-vowels, and the fourth must be a digit (![]() through
through ![]() ). If the symbols are chosen at random subject to these conditions, what is the probability that the plate will read "
). If the symbols are chosen at random subject to these conditions, what is the probability that the plate will read "![]() "?
"? ![]()
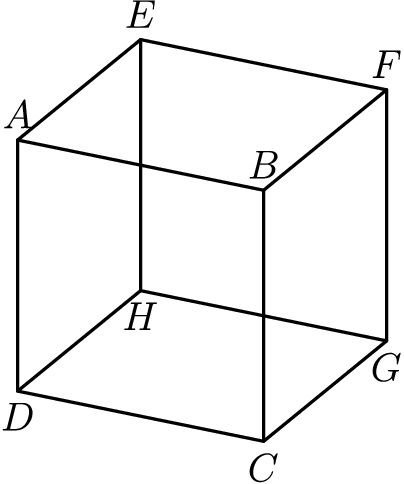
Problem 12
How many pairs of parallel edges, such as ![]() and
and ![]() or
or ![]() and
and ![]() , does a cube have?
, does a cube have?
![]()
Problem 13
How many subsets of two elements can be removed from the set ![]() so that the mean (average) of the remaining numbers is
so that the mean (average) of the remaining numbers is ![]() ?
? ![]()
Problem 14
Which of the following integers cannot be written as the sum of four consecutive odd integers? ![]()
Problem 15
At Euler Middle School, ![]() students voted on two issues in a school referendum with the following results:
students voted on two issues in a school referendum with the following results: ![]() voted in favor of the first issue and
voted in favor of the first issue and ![]() voted in favor of the second issue. If there were exactly
voted in favor of the second issue. If there were exactly ![]() students who voted against both issues, how many students voted in favor of both issues?
students who voted against both issues, how many students voted in favor of both issues? ![]()
Problem 16
In a middle-school mentoring program, a number of the sixth graders are paired with a ninth-grade student as a buddy. No ninth grader is assigned more than one sixth-grade buddy. If ![]() of all the ninth graders are paired with
of all the ninth graders are paired with ![]() of all the sixth graders, what fraction of the total number of sixth and ninth graders have a buddy?
of all the sixth graders, what fraction of the total number of sixth and ninth graders have a buddy? ![]()
Problem 17
Jeremy's father drives him to school in rush hour traffic in ![]() minutes. One day there is no traffic, so his father can drive him
minutes. One day there is no traffic, so his father can drive him ![]() miles per hour faster and gets him to school in
miles per hour faster and gets him to school in ![]() minutes. How far in miles is it to school?
minutes. How far in miles is it to school? ![]()
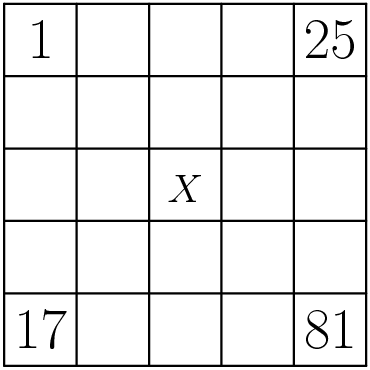
Problem 18
An arithmetic sequence is a sequence in which each term after the first is obtained by adding a constant to the previous term. For example, ![]() is an arithmetic sequence with five terms, in which the first term is
is an arithmetic sequence with five terms, in which the first term is ![]() and the constant added is
and the constant added is ![]() . Each row and each column in this
. Each row and each column in this ![]() array is an arithmetic sequence with five terms. What is the value of
array is an arithmetic sequence with five terms. What is the value of ![]() ?
? 
![]()
Problem 19
A triangle with vertices as ![]() ,
, ![]() , and
, and ![]() is plotted on a
is plotted on a ![]() grid. What fraction of the grid is covered by the triangle?
grid. What fraction of the grid is covered by the triangle? 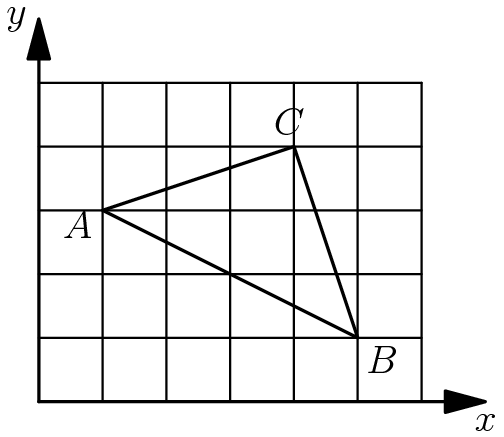
![]()
Problem 20
Ralph went to the store and bought ![]() pairs of socks for a total of
pairs of socks for a total of ![]() . Some of the socks he bought cost
. Some of the socks he bought cost ![]() a pair, some of the socks he bought cost
a pair, some of the socks he bought cost ![]() a pair, and some of the socks he bought cost
a pair, and some of the socks he bought cost ![]() a pair. If he bought at least one pair of each type, how many pairs of
a pair. If he bought at least one pair of each type, how many pairs of ![]() socks did Ralph buy?
socks did Ralph buy? ![]()
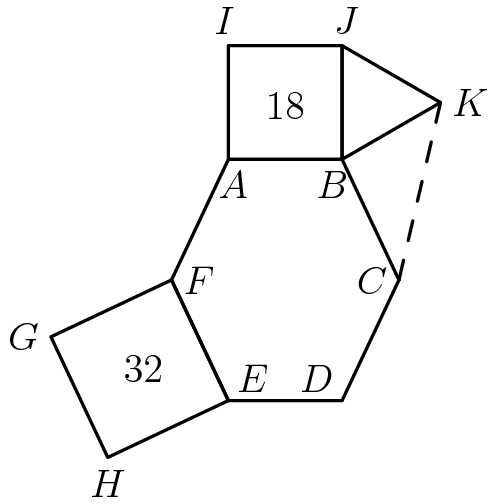
Problem 21
In the given figure hexagon ![]() is equiangular,
is equiangular, ![]() and
and ![]() are squares with areas
are squares with areas ![]() and
and ![]() respectively,
respectively, ![]() is equilateral and
is equilateral and ![]() . What is the area of
. What is the area of ![]() ?
? 
![]()
Problem 22
On June ![]() , a group of students are standing in rows, with
, a group of students are standing in rows, with ![]() students in each row. On June
students in each row. On June ![]() , the same group is standing with all of the students in one long row. On June
, the same group is standing with all of the students in one long row. On June ![]() , the same group is standing with just one student in each row. On June
, the same group is standing with just one student in each row. On June ![]() , the same group is standing with
, the same group is standing with ![]() students in each row. This process continues through June
students in each row. This process continues through June ![]() with a different number of students per row each day. However, on June
with a different number of students per row each day. However, on June ![]() , they cannot find a new way of organizing the students. What is the smallest possible number of students in the group?
, they cannot find a new way of organizing the students. What is the smallest possible number of students in the group? ![]()
Problem 23
Tom has twelve slips of paper which he wants to put into five cups labeled ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . He wants the sum of the numbers on the slips in each cup to be an integer. Furthermore, he wants the five integers to be consecutive and increasing from
. He wants the sum of the numbers on the slips in each cup to be an integer. Furthermore, he wants the five integers to be consecutive and increasing from ![]() to
to ![]() . The numbers on the papers are
. The numbers on the papers are ![]() and
and ![]() . If a slip with
. If a slip with ![]() goes into cup
goes into cup ![]() and a slip with
and a slip with ![]() goes into cup
goes into cup ![]() , then the slip with
, then the slip with ![]() must go into what cup?
must go into what cup? ![]()
Problem 24
A baseball league consists of two four-team divisions. Each team plays every other team in its division ![]() games. Each team plays every team in the other division
games. Each team plays every team in the other division ![]() games with
games with ![]() and
and ![]() . Each team plays a
. Each team plays a ![]() -game schedule. How many games does a team play within its own division?
-game schedule. How many games does a team play within its own division? ![]()
Problem 25
One-inch squares are cut from the corners of this ![]() inch square. What is the area in square inches of the largest square that can be fitted into the remaining space?
inch square. What is the area in square inches of the largest square that can be fitted into the remaining space? 
![]()
请点击2015AMC8答案查看选项答案
以上解析方式仅供参考
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1