- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2022年AMC12A卷真题答案及解析!(附AIME课程辅导)
作为全球影响力最大,适配范围最广的数学学术活动,美国AMC学术活动被越来越多的家庭选择并参加。AMC作为全球信任度最高的数学学术活动,名校都高看一眼,如果能够拿到奖项,对申请的意义自然不言而喻。从小学到高中,全球有近几十个国家和3000所学校的学生角逐于这场学术活动。
2022年AMC10/12A、B卷都考完了,中国赛区作为全球最后一个进行考试的主要赛区也正式拉下帷幕!同学们纷纷前来反馈,对题目难度的感叹各有不同!
大家关心的AMC12 A卷答案+解析来了!同学们可以核对一下答案,预测一下自己的考分。无论结果好坏,它都是激励我们日后努力的契机。有希望晋级的同学,可以提前开始准备AIME考试。如果你是打算明年参赛的考生,考前一定要看看近几年真题都考了哪些知识点,难度如何,方便自己做好周全准备。

AMC12 A卷考试难度
今年的AMC12 A卷难度不大,比去年秋季A卷略难,与去年秋季B卷接近。比较有意思的是,今年AMC12 A卷-24题与AMC10 A卷-24题一样,很难不让人觉得考官在偷懒摸鱼哟。
代数依旧占据绝大部分,其他模块考察比重接近。计算量中等。1-2属于送分题,3-15难度基本很接近属于中等难度题,16-22属于偏难题,23-25属于难题。
绝大部分知识点在往年的真题中都有出现过,所以如果平时基础不错,准备又很充分的学生,应该都能轻松应对!
扫码免费领取AMC12历年真题及答案
扫码获取【2022最新AMC12真题+答案+视频解析】
AMC12 A卷真题+解析
Problem1
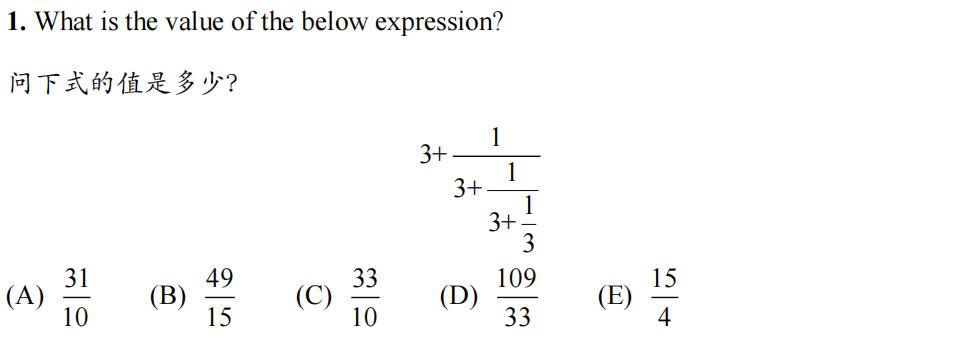
【答案】D
【考点】代数(基本运算)
【难度】1
【解析】通分计算即可
Problem2

【答案】E
【考点】代数(基本运算)
【难度】1
【解析】根据题目条件列出方程,a+b+c= 96;a=6c;c= b-40,解得a=42,b=47,c=7。
Problem3
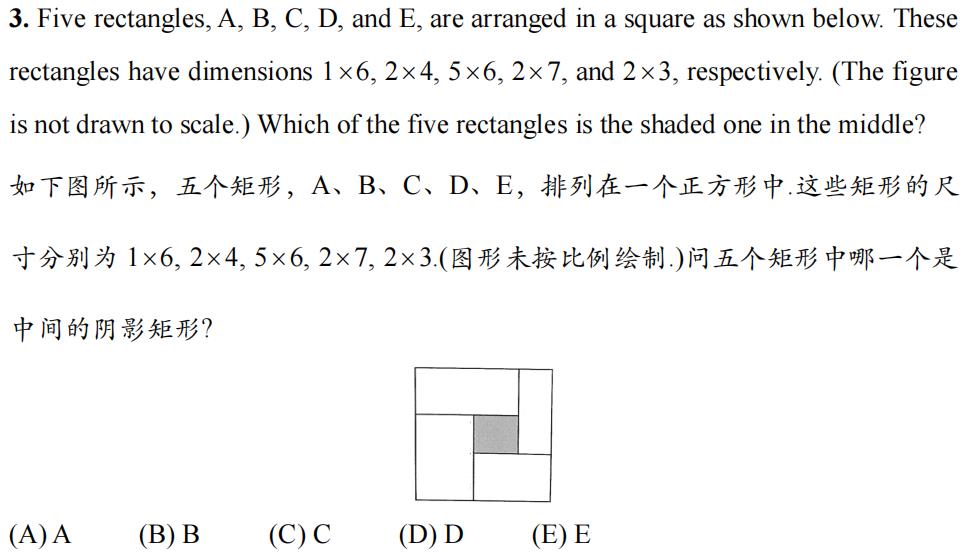
【答案】B
【考点】几何(边长计算)
【难度】2
【解析】 10条边的和为1+6+2+4+5+6+2+7+2+3=38.减去中间长方形的2条边后等于正方形的周长,应该是4的倍数,所以只能是2x4在中间。
Problem4

【答案】B
【考点】数论(质因数分解(LCMGCD))
【难度】2
【解析】假设n=2a3b5c(由LCM可知n不可能含有别的质因子),根据题目条件列出方程,lcm(2a3b5c ,2132)=223251;gcd(2a3b5c,3251)=3151,根据GCD和LCM的定义(对于每一个质数,分别取指数的最小值和最大值),易求得c=1,b=1,a=2,从而n= 60。
Problem5

【答案】C
【考点】组合(基本计数方法)
【难度】2
【解析】要求的点P(x,y)需要满足|x|+|y|≤20,根据对称性,可以分以下情况讨论:
Case 1:x=y=0;
Case 2:x,y恰好1和为0,此时共有2*2*20= 80;
Case 3:x,y都不为0, 则共有4(1+2+3+…+19)= 760 ;
综上,共有841个点。
AMC12 A卷真题答案
1-5:DEBBC
6-10:DDAAE
11-15:EBACD
16-20:DAADB
21-25:EADEE
因篇幅有限,仅展示部分真题解析
完整版真题及答案解析,可以添加【文中二维码】免费领取~
推荐阅读:
翰林数学学术活动辅导课程火热招生中!
班课和VIP(1V1)课程均已开放报名,欢迎扫文中二维码联系翰林顾问老师预约,先到先得。
AIME参赛资格(满足一个即可):
1、AMC12测试得分(总分150分)>100
2、AMC10测试中成绩在所有参赛者中排名前2.5%
3、成绩在所有参赛者中排名前5%
AIME学术活动时间:
AIME I 2023年2月7日,星期二,东部时间13:30-17:30
AIME II 2023年2月15日,星期三,东部时间13:30-17:30
AIME学术活动难度:
AIME学术活动通常前几题难度大致相当于AMC 12的水平,而越往后题目难度越大。通常多数学生能做出第1-5题;到了第6-10题则是区分度最大的题,经过专门的训练、在AMC12或AMC10中排名前1%左右的选手一般能做对一部分题;而一般在考场上能做出第11-15题都是极其顶尖的选手。
AIME课程安排:
开课测试和题目选讲
1、进阶代数第一部分 对数、三角函数、复数
2、进阶代数第二部分 多项式、不等式、数列
3、方法论第一部分 不变性原理
真题测试解析
1、进阶几何第一部分 三角形、射影几何
2、 进阶几何第二部分 圆、根轴
3、方法论第二部分 对称性原理、几何技巧
真题测试解析
1、进阶数论第一部分 高次余数、费马小定理、费马-欧拉定理
2、进阶数论第二部分 丢番图方程
3、方法论第三部分 极限、构造方程
真题测试解析
1、进阶排列组合第一部分 枚举
2、 进阶排列组合第二部分 递推
3、 方法论第四部分 其他方法
真题测试解析
1、综合第一部分
2、综合第二部分
3、考前测试和考试注意事项
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





