- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
OCR A Level Biology:复习笔记1.1.5 Presenting Experimental Data
Presenting Experimental Data
- There are many different types of experiments that can be conducted in biology
- The data collected from biological experiments can vary greatly across the subject
- For example, the large amounts of numerical data produced from ecological studies is very different to the drawings produced from microscope slides of live specimens
- The nature of an experiment dictates how the data should be presented
- It is important that scientists can make the correct judgment when deciding how to present data from an experiment
Collecting data
- Qualitative experiments involve collecting and recording observations
- Quantitative experiments involve collecting and recording numerical data
- Recording experimental data in a table is important for any type of experiment
- The table used will vary considerably depending on the specific requirements
- When constructing such a table:
- Draw lines with a ruler to separate cells
- Use appropriate headings
- Use the correct units and symbols (in the headings, not the cells)
- The independent variable should be in the first column
- Any dependent variable readings should be in the subsequent columns
Examples of a table that has been correctly constructed for an experiment
Processing data
- Depending on the type of experiment, data is processed using different methods (before being analysed)
- Some data does not require any processing, like drawings from life
- Qualitative results can't be processed mathematically (there isn't any numerical data) but the observations can be analysed
- The observations may be compared to a standard or other experimental work
- Quantitative results must be processed using mathematical skills prior to analysis
- Simple calculations work out means and rates
- Further calculations are done to obtain information surrounding means (standard deviation and standard error)
- Statistical tests are performed to better understand the results (chi-squared and t-test etc.)
- In addition to these mathematical calculations, the data can be presented in graphical form
- Graphs, bar charts, and histograms can be used to display quantitative data
- The type of graphical format used depends on the data
- For qualitative and discrete data, bar charts or pie charts are most suitable
- For continuous data, line graphs or scatter graphs are most suitable
- Any graph drawn should have:
- The appropriate scale with equal intervals
- Labelled axes with the correct units
- Straight lines drawn with a ruler
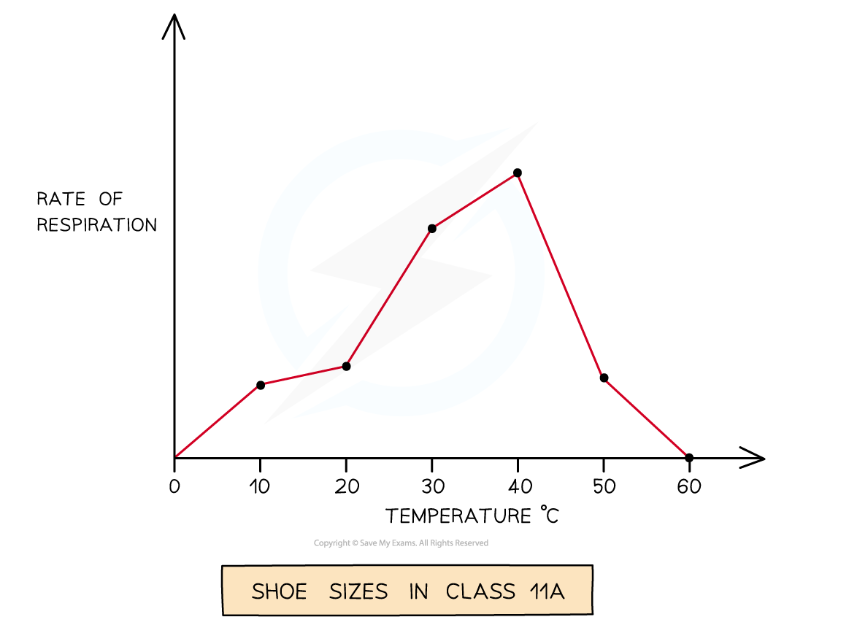
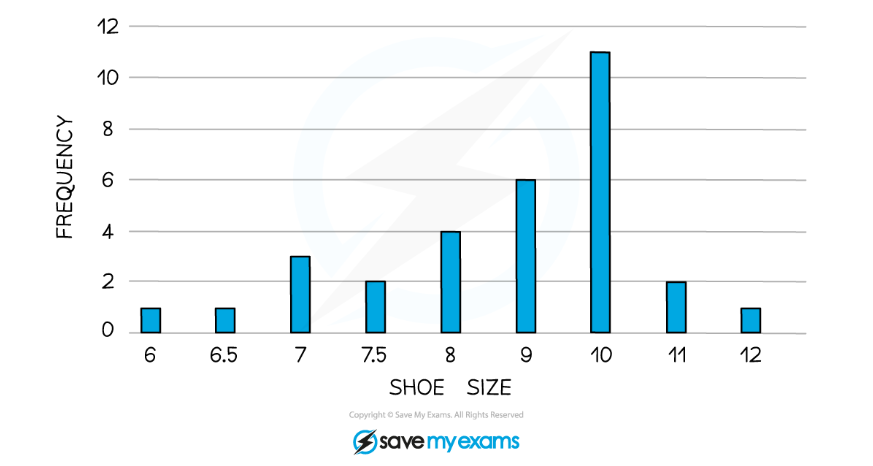
The line graph has been used to display continuous data over time while the bar chart has been used to display grouped data
Precision & Accuracy
- The certainty of any conclusions made from an experiment are impacted by the precision and accuracy of measurements and data
- It is a very common mistake to confuse precision with accuracy – measurements can be precise but not accurate if each measurement reading has the same error
- Precision refers to the ability to take multiple readings with an instrument that are close to each other, whereas accuracy is the closeness of those measurements to the true value
Precision
- Precise measurements are ones in which there is very little spread about the mean value, in other words, how close the measured values are to each other
- If a measurement is repeated several times, it can be described as precise when the values are very similar to, or the same as, each other
- The precision of a measurement is reflected in the values recorded – measurements to a greater number of decimal places are said to be more precise than those to a whole number
- Random errors cause unpredictable fluctuations in an instrument’s readings as a result of uncontrollable factors, such as environmental conditions
- This affects the precision of the measurements taken, causing a wider spread of results about the mean value
- To reduce random error:
- Repeat measurements several times and calculate an average from them
Accuracy
- A measurement is considered accurate if it is close to the true value
- Systematic errors arise from the use of faulty instruments used or from flaws in the experimental method
- This type of error is repeated consistently every time the instrument is used or the method is followed, which affects the accuracy of all readings obtained
- To reduce systematic errors:
- Instruments should be recalibrated, or different instruments should be used
- Corrections or adjustments should be made to the technique
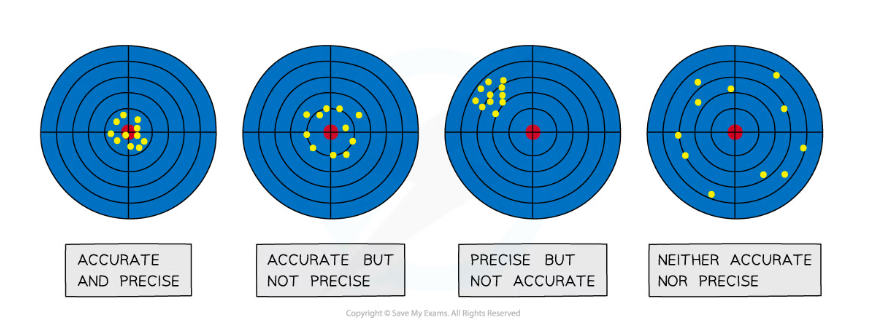
The difference between precise and accurate results
Uncertainty
- Measurements of quantities are made with the aim of finding the true value of that quantity
- In reality, it is impossible to obtain the true value of any quantity as there will always be a degree of uncertainty
- Uncertainty is the amount of error your measurements might contain
- Results from experiments always contain some error (they are never perfect)
- There will always be a small degree of uncertainty in your readings or measurements
- This is often because the accuracy and precision of the apparatus being used is limited
- The margins of error of the apparatus are usually displayed on the glassware
- These margins of error can be used to calculate percentage error
- Percentage error helps to quantify the margin of error and its possible impact on the results
- For example, you may want to measure a reaction rate by measuring how much of a product is made in a given time period (e.g. using a gas syringe to measure the volume of oxygen produced from the breakdown of hydrogen peroxide by catalase)
- The gas syringe may only give readings to the nearest 1 cm3
- The gas syringe has a margin of error of ± 0.05 cm3
- A ‘±’ sign tells you the range in which the true value lies
- The real volume produced could be up to 0.05 cm3 smaller or larger
- For experiments, you may need to calculate the percentage error of your measurements
- As long as you know the uncertainty value of your measurements, the percentage error can be calculated using the following formula:
percentage error = (uncertainty value ÷ your measurement) x 100
- A percentage error less than 5% is considered statistically not significant
Choosing the apparatus with the right resolution
- Resolution is the smallest change in the quantity being measured of a measuring instrument that gives a perceptible change in the reading
- For example, the resolution of a wristwatch is 1 s, whereas the resolution of a digital stop-clock is typically 10 ms (0.01 s)
- In imaging, resolution can also be described as the ability to see two structures as two separate structures rather than as one fuzzy entity
- When choosing measuring instruments, instruments with an appropriate measuring scale need to be used
- Smaller measuring instruments have higher resolution scales due to the smaller graduations on the scale. This means they have smaller margins of error
- For example, measuring 5 cm3 of a liquid using a 500 cm3 measuring cylinder would be very difficult. A 10cm3 measuring cylinder would be a more appropriate choice as the measuring scale is of a higher resolution
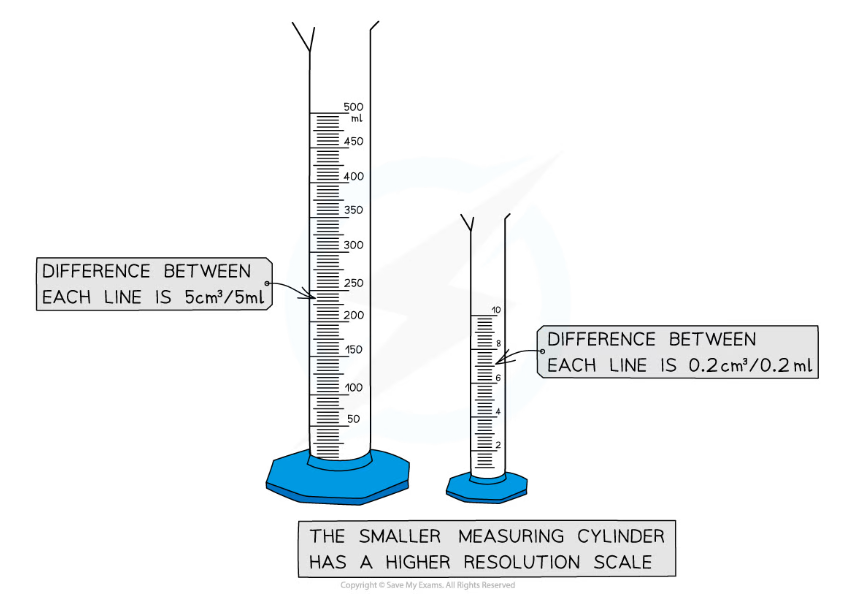
Smaller measuring instruments tend to have higher resolution measurements and a smaller margin of error. Make sure to always choose the appropriate instrument for the experiment
Worked Example
In an enzyme rate reaction involving the breakdown of hydrogen peroxide by catalase, 50 cm3 of oxygen was produced, with an uncertainty value of 0.05 cm3. Calculate the percentage error of this measurement.
Percentage error = (uncertainty value ÷ your measurement) x 100
Percentage error = (0.05 ÷ 50) x 100
Percentage error = 0.001 x 100
Percentage error = 0.1%
Worked Example
In an enzyme rate experiment involving the breakdown of hydrogen peroxide by catalase, a student recorded that 10 cm3 of oxygen was produced in 5.245 seconds. The student measured this using a stopwatch that counted in milliseconds. Calculate the percentage error of the stopwatch measurements.
Step 1: Calculate the uncertainty value
The stopwatch can measure to the nearest millisecond (0.001 seconds)
This means the actual time taken could be up to 0.0005 seconds shorter or longer than this
This means stopwatch measurements have an uncertainty value of ± 0.0005 s
Step 2: Calculate the percentage error of the student’s measurement of 5.245 seconds
Percentage error = (uncertainty value ÷ your measurement) x 100
Percentage error = (0.0005 ÷ 5.245) x 100
Percentage error = 0.000095 x 100
Percentage error = 0.0095% or 0.01%
Qualitative and Quantitative Results
- There are two types of experiment, which in turn obtain two kinds of results:
- Qualitative experiments are used to obtain qualitative results
- Observations are recorded without collecting numerical data
- For example, the starch test using iodine is a qualitative test - a colour change is recorded
- Other common qualitative measurements include smells, tastes, textures, sounds and descriptions of the weather or of a particular habitat
- Quantitative experiments are used to obtain quantitative results
- Numerical data is collected and recorded
- For example, recording the percentage cover of a plant species using a quadrat - a numerical value (a percentage) is recorded
- Other common quantitative measurements include temperature, pH, time, volume, length and mass
- In order to collect numerical data, a quantitative experiment must use apparatus that measures or collects this type of data
Recording qualitative and quantitative results
- Qualitative results are most often recorded in the form of words, short sentences and descriptions, such as describing a colour change, making a note of someone's opinion, describing the appearance or behaviour of an organism, or describing a chemical reaction
- Quantitative results must all be recorded to the same number of decimal places but processed data can be recorded to the same number of decimal places or to one more decimal place than the raw data
- For example, the mean of 11, 12 and 14 can be recorded as 12 or 12.3 but not 12.3333333
Reaching valid conclusions from qualitative and quantitative results
- It could be argued that qualitative results can be more subjective (i.e. influenced by the person making the observations), but in fact, both types of results are subject to bias and error
- Tools and systems for data gathering and recording are important for both
- Care should be taken when making qualitative observations to keep them as objective as possible (i.e. not allowing observations to be influenced by the person making them)
- In terms of scientific research (and especially in biological experiments sometimes), one type of results is not necessarily better than the other
- The value of qualitative and quantitative data depends on the thing being observed and the purpose of the experiment
- Sometimes it’s important and very useful to use both
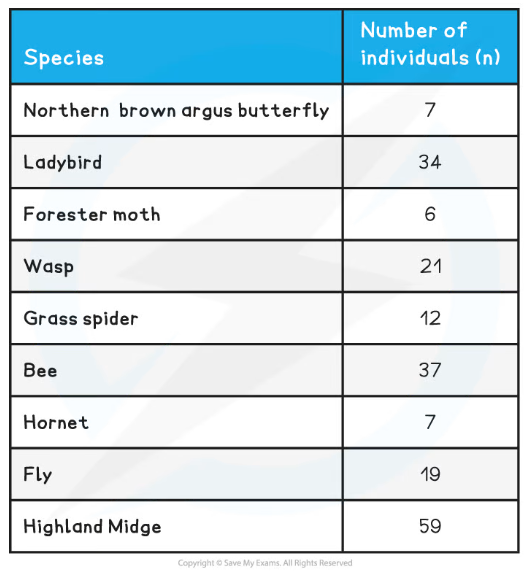
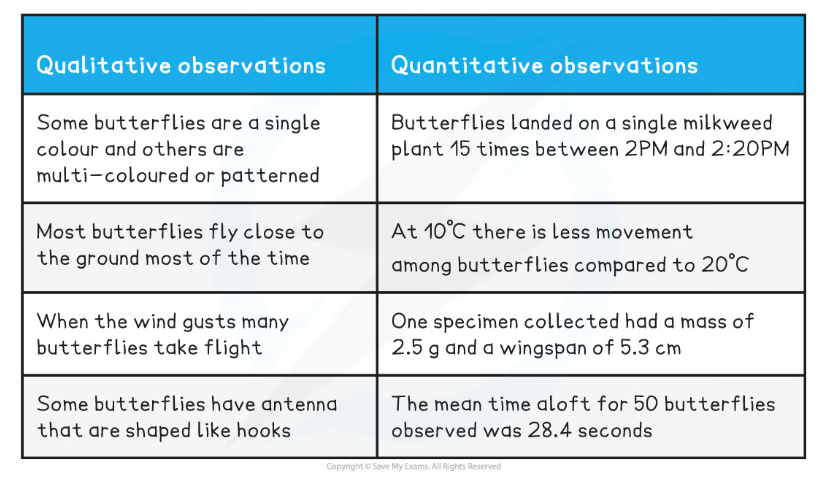
- In the example table below, both qualitative and quantitative observations have been recorded whilst observing a field of butterflies and both sets of observations can be useful in drawing conclusions (although as always, the validity of any conclusions drawn can be increased by repeating the experiments and gathering more data)
Qualitative and Quantitative Observations Table
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





