- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Maths: Statistics:复习笔记4.3.3 Standard Normal Distribution
Standard Normal Distribution
What is the standard normal distribution?
- The standard normal distribution is a normal distribution where the mean is 0 and the standard deviation is 1
- It is denoted by Z
-
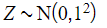
Why is the standard normal distribution important?
- Any normal distribution curve can be transformed to the standard normal distribution curve by a horizontal translation and a horizontal stretch
- Therefore we have the relationship:
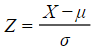
- Where
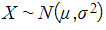 and
and 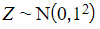
- Probabilities are related by:
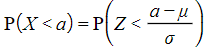
- This will be useful when the mean or variance is unknown
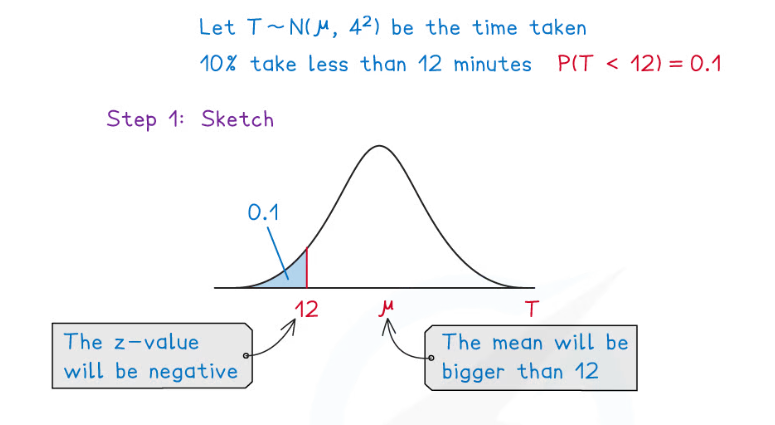
- If a value of x is less than the mean then the z-value will be negative
- Some mathematicians use the function
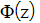 to represent
to represent 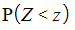
The table of percentage points of the normal distribution
- In your formula booklet you have the table of percentage points which provides information about specific values of the standard normal distribution that correspond to commonly used probabilities
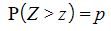
- You are given the value of to 4 decimal places when p is:
- 0.5, 0.4, 0.3, 0.2, 0.15, 0.1, 0.05, 0.025, 0.01, 0.005, 0.001, 0.005
- These values of z can be found using the "Inverse Normal Distribution" function on your calculator
- If you are happy using your calculator then you can simply ignore this table
- They are simply listed in your formula booklet as they are commonly used when:
- Finding an unknown mean and/or variance for a normal distribution
- Performing a hypothesis test on the mean of a normal distribution
Finding Sigma and Mu
How do I find the mean (μ) or the standard deviation (σ) if one of them is unknown?
- If the mean or standard deviation of the
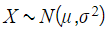 is unknown then you will need to use the standard normal distribution
is unknown then you will need to use the standard normal distribution - You will need to use the formula
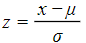 or its rearranged form
or its rearranged form 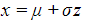
- You will be given a probability for a specific value of
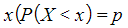 or
or 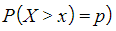
- To find the unknown parameter:
- STEP 1: Sketch the normal curve
- Label the known value and the mean
- STEP 2: Find the z-value for the given value of x
- Use the Inverse Normal Distribution to find the value of z such that
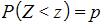 or
or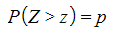
- Make sure the direction of the inequality for Z is consistent with X
- Try to use lots of decimal places for the z-value to avoid rounding errors
- You should use at least one extra decimal place within your working than your intended degree of accuracy for your answer
- Use the Inverse Normal Distribution to find the value of z such that
- STEP 3: Substitute the known values into
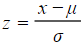 or
or 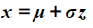
- You will be given x and one of the parameters (μ or σ) in the question
- You will have calculated z in STEP 2
- STEP 4: Solve the equation
How do I find the mean (μ) and the standard deviation (σ) if both of them are unknown?
- If both of them are unknown then you will be given two probabilities for two specific values of x
- The process is the same as above
- You will now be able to calculate two z-values
- You can form two equations (rearranging to the form
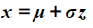 is helpful)
is helpful) - You now have to solve the two equations simultaneously (you can use your calculator to do this)
- Be careful not to mix up which z-value goes with which value of
Worked Example
It is known that the times, in minutes, taken by students at a school to eat their lunch can be modelled using a normal distribution with standard deviation 4 minutes.
Given that 10% of students at the school take less than 12 minutes to eat their lunch, find the mean time taken by the students at the school.
Exam Tip
- These questions are normally given in context so make sure you identify the key words in the question. Check whether your z-values are positive or negative and be careful with signs when rearranging.
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1