- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Maths: Statistics:复习笔记4.3.2 Normal Distribution - Calculations
Throughout this section we will use the random variable ![]() . For a normal distribution, X can take any real number. Therefore any values mentioned in this section will be assumed to be real numbers.
. For a normal distribution, X can take any real number. Therefore any values mentioned in this section will be assumed to be real numbers.
Calculating Normal Probabilities
How do I find probabilities using a normal distribution?
- The area under a normal curve between the points
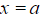 and
and 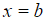 is equal to the probability
is equal to the probability 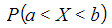
- Remember for a normal distribution
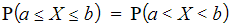 so you do not need to worry about whether the inequality is strict (< or >) or weak (≤ or ≥)
so you do not need to worry about whether the inequality is strict (< or >) or weak (≤ or ≥)
- Remember for a normal distribution
- The equation of a normal distribution curve is complicated so the area must be calculated numerically
- You will be expected to use distribution functions on your calculator to find the probabilities when working with a normal distribution
How do I calculate, P(X = x) ,the probability of a single value for a normal distribution?
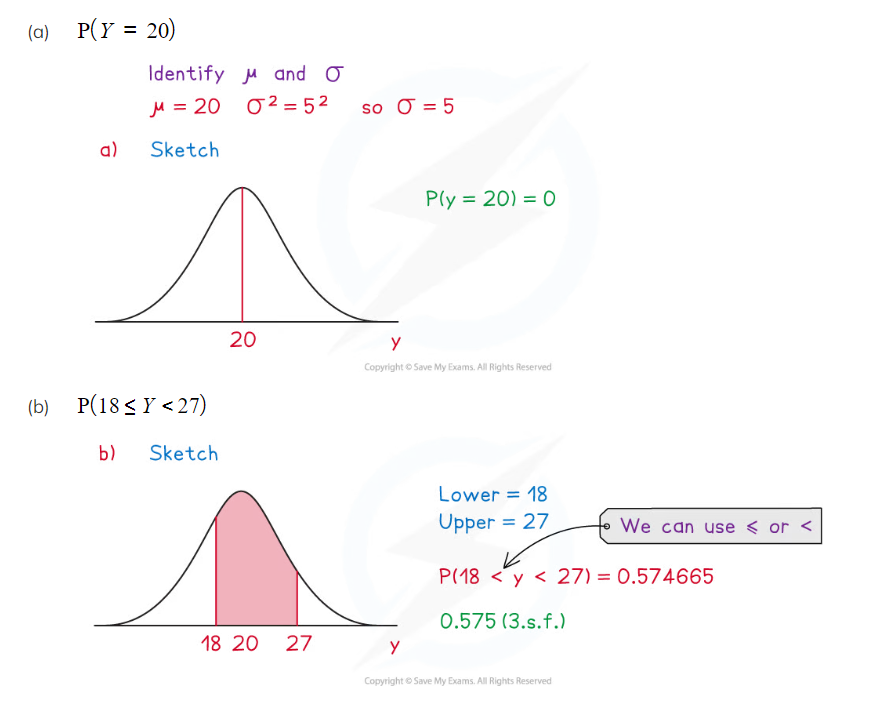
- The probability of a single value is always zero for a normal distribution
- You can picture this as the area of a single line is zero
- P(X = x ) = 0
- Your calculator is likely to have a "Normal Probability Density" function
- This is sometimes shortened to NPD, Normal PD or Normal Pdf
- IGNORE THIS FUNCTION for this course!
- This calculates the probability density function at a point NOT the probability
How do I calculate, P(a < X < b) the probability of a range of values for a normal distribution?
- You need a calculator that can calculate cumulative normal probabilities
- You want to use the "Normal Cumulative Distribution" function
- This is sometimes shortened to NCD, Normal CD or Normal Cdf
- You will need to enter:
- The 'lower bound' - this is the value a
- The 'upper bound' - this is the value b
- The 'µ' value - this is the mean
- The 'σ' value - this is the standard deviation
- Check the order carefully as some calculators ask for standard deviation before mean
- Remember it is the standard deviation (so if you have the variance then square root it)
- Always sketch a quick diagram to visualise which area you are looking for
How do I calculate, P(X>a) or P(X<b) for a normal distribution?
- You will still use the "Normal Cumulative Distribution" function
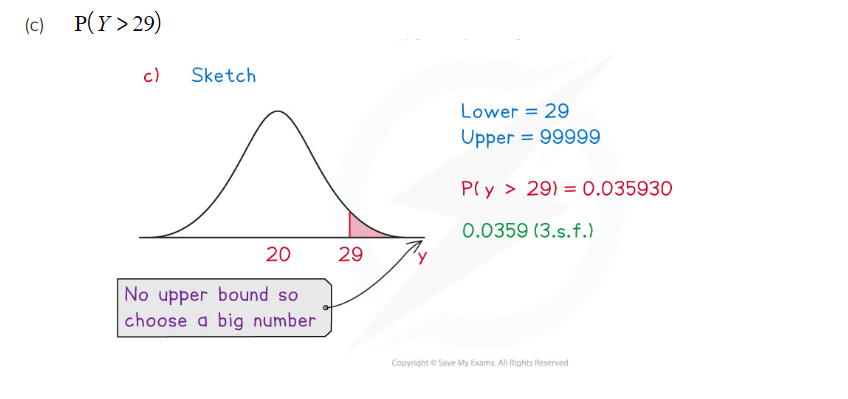
- P(X > a) can be estimated using an upper bound that is sufficiently bigger than the mean
- Using a value that is more than 4 standard deviations bigger than the mean is quite accurate
- Or an easier option is just to input lots of 9's for the upper bound (99999999.. or 1099)
- Similarly P(X < b) can be estimated using a lower bound that is sufficiently smaller than the mean
- Using a value that is more than 4 standard deviations smaller than the mean is quite accurate
- Or an easier option is just to input lots of 9's for the lower bound with a negative sign (-99999999... or -1099)
- This works because the probability that X is more than 3 standard deviations bigger than the mean is less than 0.0015
- This is the same for being 3 standard deviations less than the mean
- This reduces to less than 0.000032 when using 4 standard deviations
Are there any useful identities?
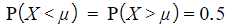
- As
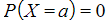 you can use:
you can use:
- These are useful when:
- The mean and/or standard deviation are unknown
- You only have a diagram
- You are working with the inverse distribution
Worked Example
The random variable ![]() . Calculate:
. Calculate:
(a)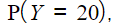
(b)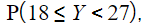
(c)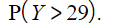
Inverse Normal Distribution
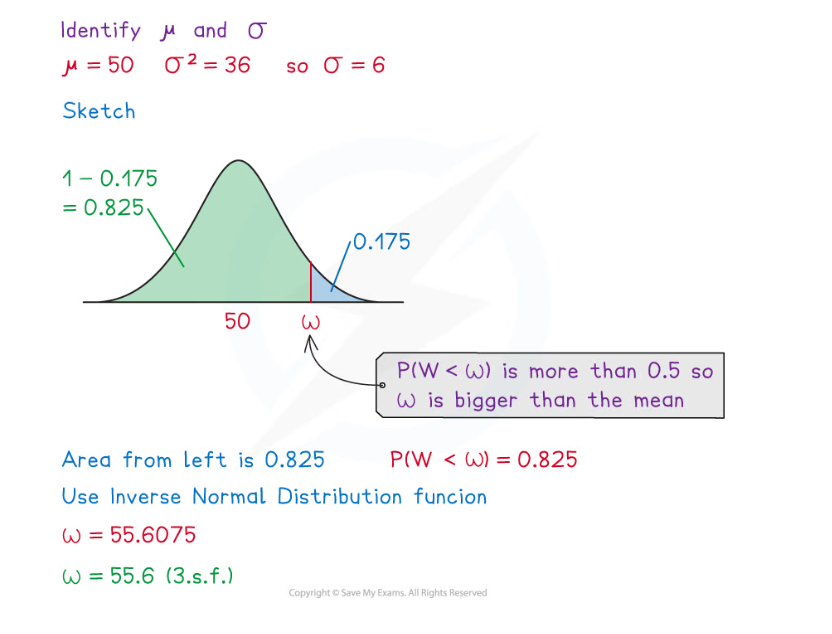
Given the value of P(X < a) how do I find the value of a ?
- Your calculator will have a function called "Inverse Normal Distribution"
- Some calculators call this InvN
- Given that P(X < a) = p you will need to enter:
- The 'area' - this is the value p
- Some calculators might ask for the 'tail' - this is the left tail as you know the area to the left of a
- The 'μ' value - this is the mean
- The 'σ' value - this is the standard deviation
- The 'area' - this is the value p
- Always check your answer makes sense
- If P(X < a) is less than 0.5 then a should be smaller than the mean
- If P(X < a) is more than 0.5 then a should be bigger than the mean
- A sketch will help you see this
Given the value of P(X > a) how do I find the value of a ?
- Given P(X > a) = p
- Use P(X < a) = 1 - P(X > a) to rewrite this as P(X < a) = 1 - p
- Then use the method for (X < a) to find a
- If your calculator does have the tail option (left, right or centre) then you can use the "Inverse Normal Distribution" function straightaway by:
- Selecting 'right' for the tail
- Entering the area as 'p'
Worked Example
The random variable ![]() .
.
Find the value of ![]() such that
such that ![]() .
.
Exam Tip
Always ask yourself two questions when using your calculator:
- Have you entered the mean and the standard deviation in the correct order?
- Have you entered the standard deviation correctly and not the variance?
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1