- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel IGCSE Physics: Double Science 复习笔记:7.2.2 Half-Life
Edexcel IGCSE Physics: Double Science 复习笔记:7.2.2 Half-Life
Half-Life
- It is impossible to know when a particular unstable nucleus will decay
- But the rate at which the activity of a sample decreases can be known
- This is known as the half-life
- Half-life is defined as:
The time it takes for the number of nuclei of a sample of radioactive isotopes to decrease by half
- In other words, the time it takes for the activity of a sample to fall to half its original level
- Different isotopes have different half-lives and half-lives can vary from a fraction of a second to billions of years in length
Using Half-life
- Scientists can measure the half-lives of different isotopes accurately:
- Uranium-235 has a half-life of 704 million years
- This means it would take 704 million years for the activity of a uranium-235 sample to decrease to half its original amount
- Carbon-14 has a half-life of 5700 years
- So after 5700 years, there would be 50% of the original amount of carbon-14 remaining
- After two half-lives, or 11 400 years, there would be just 25% of the carbon-14 remaining
- With each half-life, the amount remaining decreases by half

The diagram shows how the activity of a radioactive sample changes over time. Each time the original activity halves, another half-life has passed
- The time it takes for the activity of the sample to decrease from 100 % to 50 % is the half-life
- It is the same length of time as it would take to decrease from 50 % activity to 25 % activity
- The half-life is constant for a particular isotope
Calculating Half-Life
- To calculate the half-life of a sample, the procedure is:
- Measure the initial activity, A0, of the sample
- Determine the half-life of this original activity
- Measure how the activity changes with time
- The time taken for the activity to decrease to half its original value is the half-life
Worked Example
The radioisotope technetium is used extensively in medicine. The graph below shows how the activity of a sample varies with time. Determine the half-life of this material.
Determine the half-life of this material.
Step 1: Draw lines on the graph to determine the time it takes for technetium to drop to half of its original activity
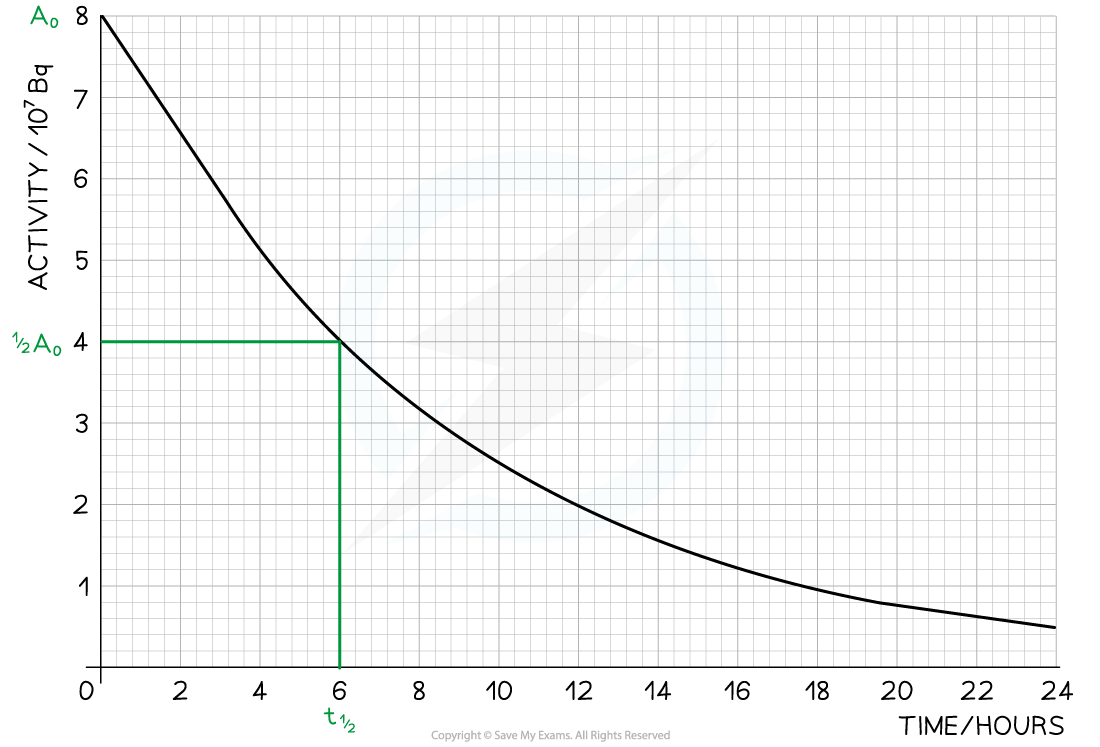
Step 2: Read the half-life from the graph
-
- In the diagram above the initial activity, A0, is 8 × 107 Bq
- The time taken to decrease to 4 × 107 Bq, or ½ A0, is 6 hours
- The time taken to decrease to 2 × 107 Bq is 6 more hours
- The time taken to decrease to 1 × 107 Bq is 6 more hours
- Therefore, the half-life of this isotope is 6 hours
Worked Example
A particular radioactive sample contains 2 million un-decayed atoms. After a year, there is only 500 000 atoms left un-decayed.What is the half-life of this material?
Step 1: Calculate how many times the number of un-decayed atoms has halved
-
- There were 2 000 000 atoms to start with
- 1 000 000 atoms would remain after 1 half-life
- 500 000 atoms would remain after 2 half-lives
- Therefore, the sample has undergone 2 half-lives
Step 2: Divide the time period by the number of half-lives
-
- The time period is a year
- The number of half-lives is 2
- 1 year divided by 2 is half a year or 6 months
- Therefore, the half-life is 6 months
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





