- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Maths: Statistics:复习笔记3.2.4 Probability Formulae
Probability Formulae
What is meant by probability formulae?
- If you have seen any of the other Revision Notes on probability, almost every one contains a formula
- These however are often disguised in Venn diagrams, tree diagrams etc
- Sometimes a diagram can be easier to use than a formula
- This Revision Note rounds up all these formulae and introduces one or two new ones
What probability formulae are there?
- Some formulae only apply under certain conditions
- The formulae for probability you should’ve encountered so far
- for independent events,
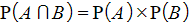 (“AND”, intersection)
(“AND”, intersection) - for mutually exclusive events,
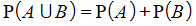 (“OR”, union)
(“OR”, union) 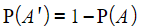 (“NOT”, complement/prime/dash)
(“NOT”, complement/prime/dash)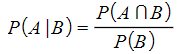 or
or 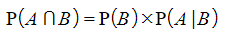
(“GIVEN THAT”)
This second version in particular is referred to as the MULTIPLICATION FORMULA (see diagram below)- For independent events,
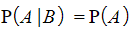
- for independent events,
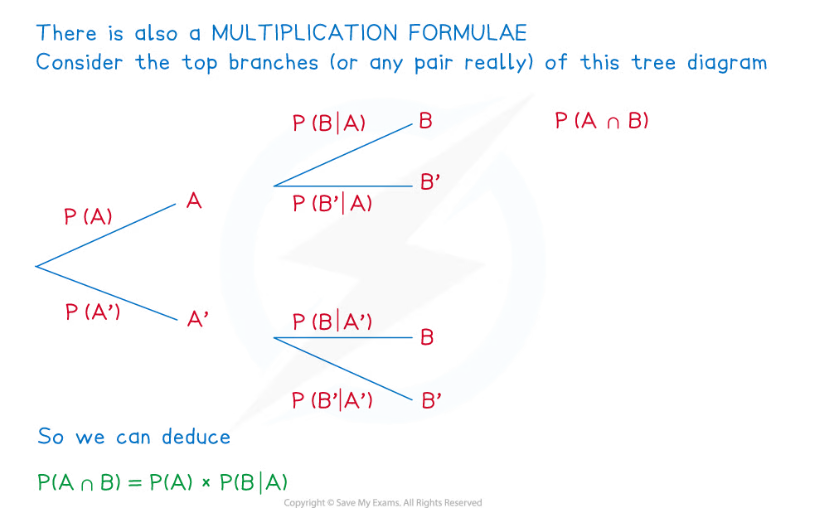
- All of the formulae above are given in the formulae booklet but some are “hidden”
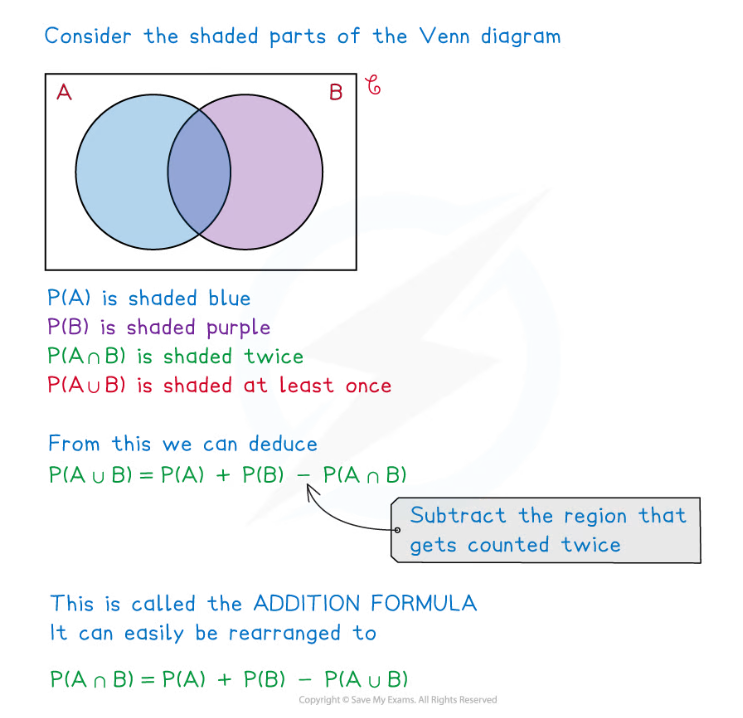
- e.g. The formulae booklet lists the addition formula
![]() but it does not list the rearranged version of it, nor does it point out that if and are mutually exclusive then
but it does not list the rearranged version of it, nor does it point out that if and are mutually exclusive then
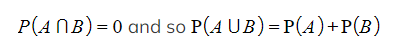
How do I solve problems using probability formulae?
- This is a combination of
- Recognising the set notation used
- Taking note of any independent or mutually exclusive events
- Using an appropriate diagram (Venn, mini-Venn, tree, two-way table)
- Converting worded questions into AND, OR, GIVEN THAT etc statements
- Knowing when a formula could be used and using the formulae booklet to double-check and confirm
- In the majority of cases a diagram can be used – so if you do not like using the formulae or find them confusing
- For events that happen in succession, use a tree diagram; Venn diagrams suit most other purposes but two-way tables can be easier to follow
- Of course, a question may give or demand the use of a particular diagram
Worked Example
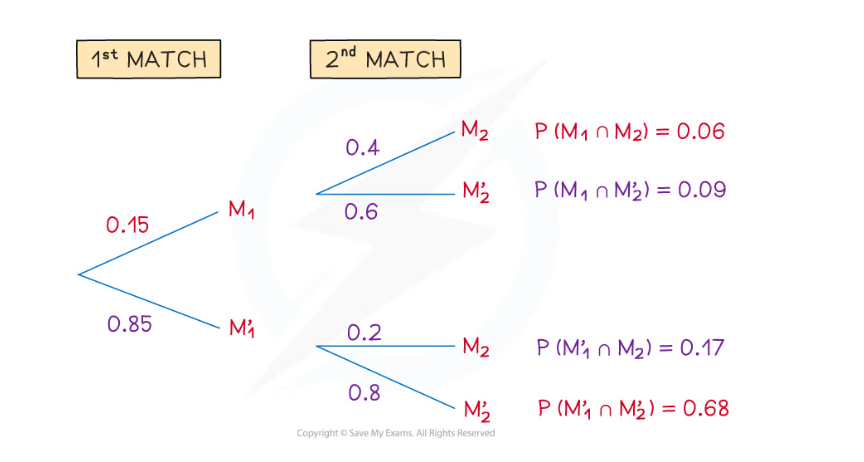
In the fictional World Stare Out Championships players compete by staring at each other with the player blinking first losing. A match cannot be drawn.
During each day of the championships three matches are scheduled to take place but if the first two matches both take more than an hour each, then the third match cannot take place that day.
A statistician notices from past fictional championship records that the probability of the first match taking longer than an hour is 0.15 and that the probability of only two matches taking place on any day is 0.06. They also notice that the probability that at least one of the first two matches takes longer than an hour is 0.32.
Find the probability that
Exam Tip
- If in any doubt always start with a diagram
- a Venn diagram can be used for most problems
- a two-way table can be easier to read if it’s possible to construct one
- a tree diagram is useful if you are looking at an event that follows another
- Remember that all probability formulae are given in the formulae booklet but not necessarily in the most user-friendly way; a quick look could just be enough to jog your memory though!
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1