- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Maths: Statistics:复习笔记3.2.3 Further Tree Diagrams
Further Tree Diagrams
What do you mean by further tree diagrams?
- The tree diagrams used here are no more complicated than those in the first Tree Diagrams revision note, however
- The wording/terminology used in questions and on diagrams may now involve the use of set notation including the symbols ∪(union), ∩(intersection) and ‘ (complement)
- e.g. P(A') would be used for “P(not A)”
- Conditional probability questions can be solved using tree diagrams
- The wording/terminology used in questions and on diagrams may now involve the use of set notation including the symbols ∪(union), ∩(intersection) and ‘ (complement)
How do I solve conditional probability problems using tree diagrams?
- Interpreting questions in terms of AND (∩), OR (∪), complement ( ‘ ) and “given that” ( | )
- Condition probability may now be involved too
- This makes it harder to know where to start and how to complete the probabilities on a tree diagram
- e.g. If given, possibly in words,
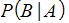 then event A has already occurred so start by looking for the branch event A in the 1st experiment, and then would be the branch for event in the 2nd experiment
then event A has already occurred so start by looking for the branch event A in the 1st experiment, and then would be the branch for event in the 2nd experiment
- e.g. If given, possibly in words,
Similarly, ![]() would require starting with event “
would require starting with event “![]() ” in the 1st experiment and event B in the 2nd experiment
” in the 1st experiment and event B in the 2nd experiment
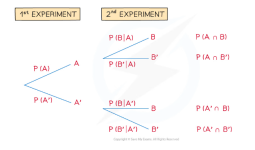
- The diagram above gives rise to some probability formulae you will see in Probability Formulae
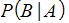 (“given that”) is the probability on the branch of the 2nd experiment
(“given that”) is the probability on the branch of the 2nd experiment- However, the “given that” statement
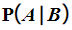 is more complicated and a matter of working backwards
is more complicated and a matter of working backwards
- from Conditional Probability,
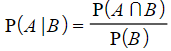
- from the diagram above,
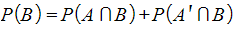
- leading to
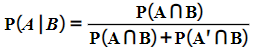
- This is quite a complicated looking formula to try to remember so use the logical steps instead – and a clearly labelled tree diagram!
- from Conditional Probability,
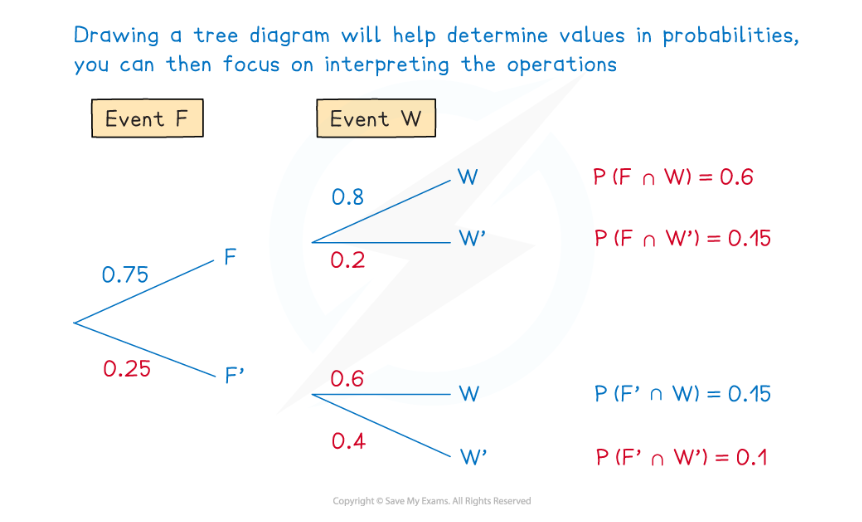
Worked Example
The event has a 75% probability of occurring.
The event ![]() follows event
follows event ![]() , and if event
, and if event ![]() has occurred, event
has occurred, event ![]() has an 80% chance of occurring.
has an 80% chance of occurring.
It is also known that ![]() .
.
Find
(i)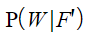
(ii)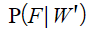
(iii)the probability that event 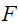 didn’t occur, given that event
didn’t occur, given that event 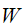 didn’t occur.
didn’t occur.

Exam Tip
- It can be tricky to get a tree diagram looking neat and clear first attempt – it can be worth drawing a rough one first, especially if there are more than two outcomes or more than two events; do keep an eye on the exam clock though!
- Always worth another mention – tree diagrams make particularly frequent use of the result
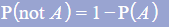
- Tree diagrams have built-in checks
- the probabilities for each pair of branches should add up to 1
- the probabilities for each outcome of combined events should add up to 1
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





