- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel IGCSE Physics: Double Science 复习笔记: 1.1.6 Area under a Velocity-Time Graph
Edexcel IGCSE Physics: Double Science 复习笔记: 1.1.6 Area under a Velocity-Time Graph
Area under a Velocity-Time Graph
- The area under a velocity-time graph represents the displacement (or distance travelled) by an object
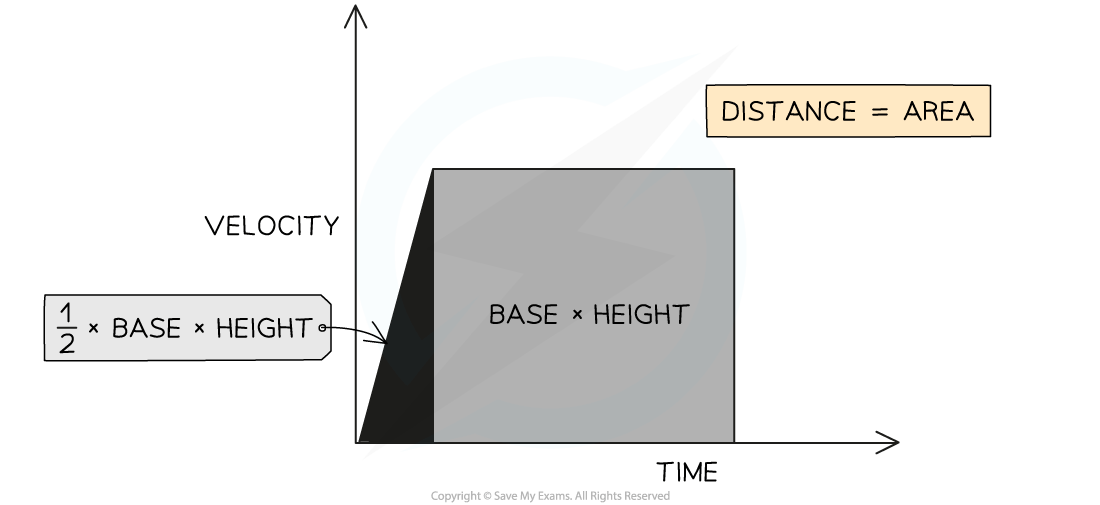
The displacement, or distance travelled, is represented by the area beneath the graph
- If the area beneath the graph forms a triangle (i.e. the object is accelerating or decelerating), then the area can be determined by using the following formula:
Area = ½ × Base × Height
- If the area beneath the graph forms a rectangle (i.e. the object is moving at a constant velocity), then the area can be determined by using the following formula:
Area = Base × Height
Determining Distance from a Velocity-Time Graph
- Enclosed areas under velocity-time graphs represent total displacement (or total distance travelled)
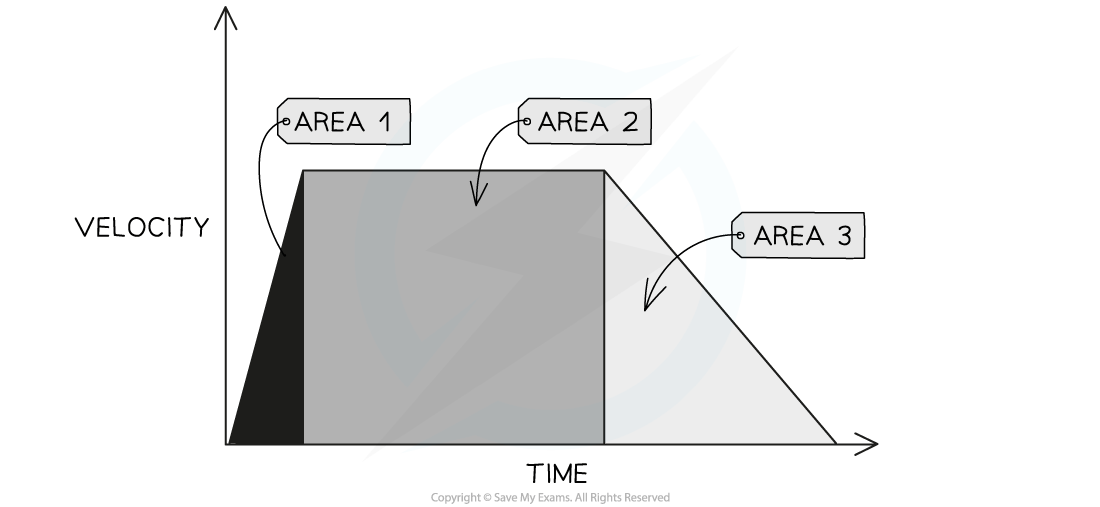
Three enclosed areas (two triangles and one rectangle) under this velocity-time graph represents the total distance travelled
- If an object moves with constant acceleration, its velocity-time graph will comprise of straight lines
- In this case, calculate the distance travelled by working out the area of enclosed rectangles and triangles as in the image above
Worked Example
The velocity-time graph below shows a car journey which lasts for 160 seconds.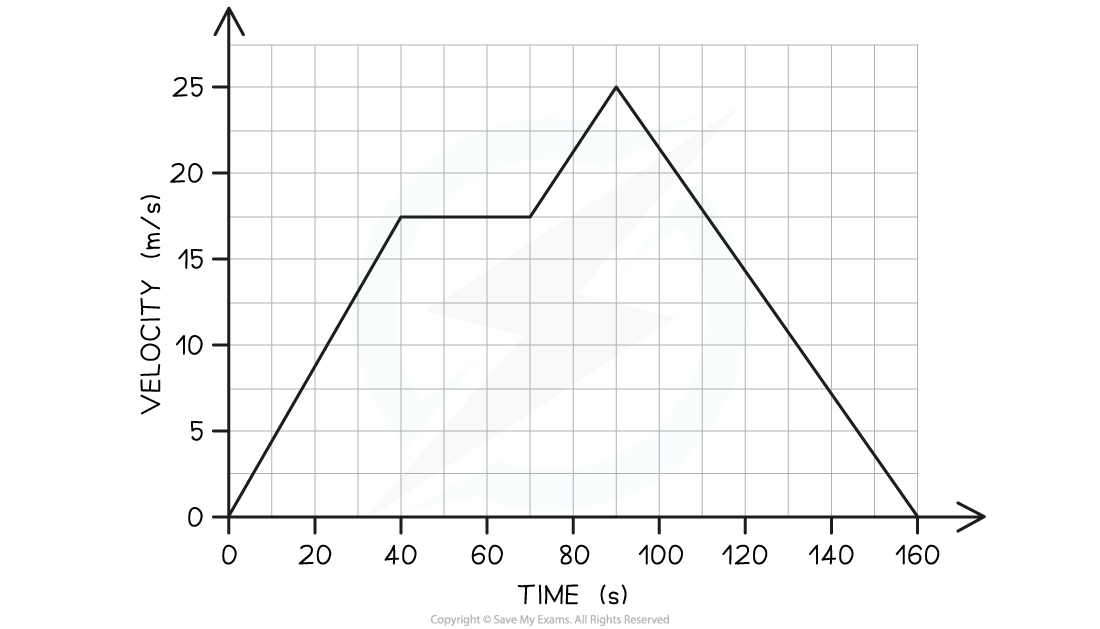 Calculate the total distance travelled by the car on this journey.
Calculate the total distance travelled by the car on this journey.
Step 1: Recall that the area under a velocity-time graph represents the distance travelled
-
- In order to calculate the total distance travelled, the total area underneath the line must be determined
Step 2: Identify each enclosed area
-
- In this example, there are five enclosed areas under the line
- These can be labelled as areas 1, 2, 3, 4 and 5, as shown in the image below:
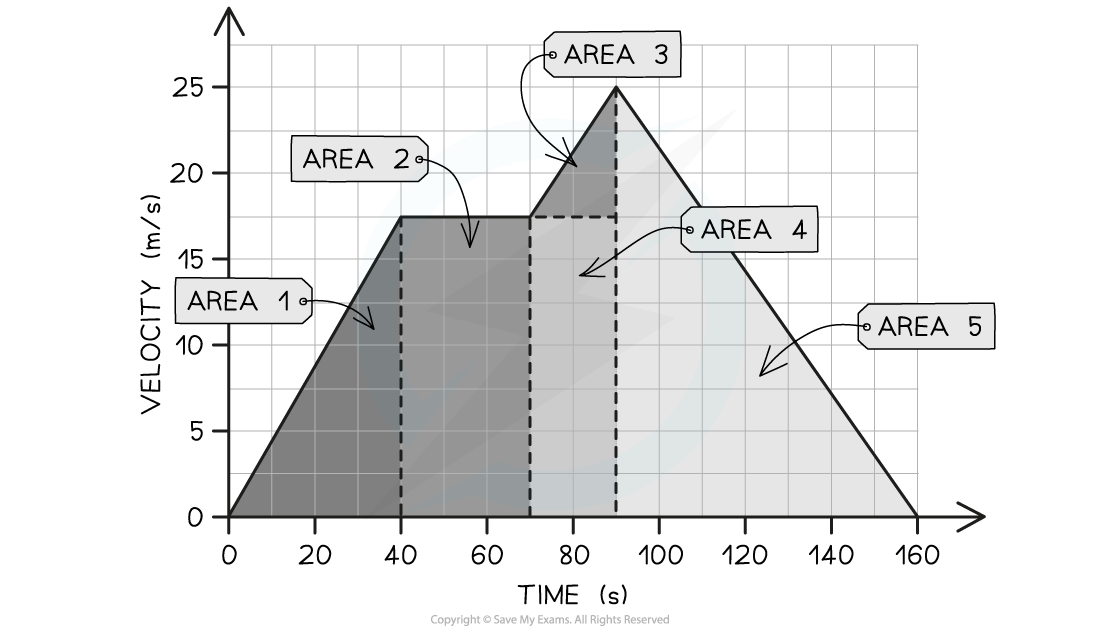
Step 3: Calculate the area of each enclosed shape under the line
-
- Area 1 = area of a triangle = ½ × base × height = ½ × 40 × 17.5 = 350 m
- Area 2 = area of a rectangle = base × height = 30 × 17.5 = 525 m
- Area 3 = area of a triangle = ½ × base × height = ½ × 20 × 7.5 = 75 m
- Area 4 = area of a rectangle = base × height = 20 × 17.5 = 350 m
- Area 5 = area of a triangle = ½ × base × height = ½ × 70 × 25 = 875 m
Step 4: Calculate the total distance travelled by finding the total area under the line
-
- Add up each of the five areas enclosed:
total distance = 350 + 525 + 75 + 350 + 875
total distance = 2175 m
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





