- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Further Maths: Core Pure:复习笔记8.3.2 Damped or Forced Harmonic Motion
Damped or Forced Harmonic Motion
What is damped harmonic motion?
- If we add a term representing a resistive force to the simple harmonic motion equation, the new equation describes a particle undergoing damped harmonic motion
- Depending on the situation being modelled, this resistive force may represent such phenomena as friction or air resistance that resist the motion of the particle
- The standard damped harmonic motion equation is of the form
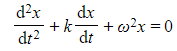
-
- Note that that is the same as the simple harmonic motion equation, except for the addition of the damping term
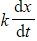
- x is the displacement of the particle from a fixed point O at time t
- k is a positive constant representing the strength of the damping force
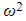 is a positive constant representing the strength of the restoring force that accelerates the particle back towards point O
is a positive constant representing the strength of the restoring force that accelerates the particle back towards point O
- Note that that is the same as the simple harmonic motion equation, except for the addition of the damping term
- The damped harmonic motion equation is a second order homogeneous differential equation, and may be solved using the standard methods for such equations
- This will involve using the auxiliary equation to find the complementary function for the equation
- You should, however, be familiar with the three main cases:
- CASE 1:
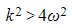
- The auxiliary equation has two distinct real roots, both of which are negative
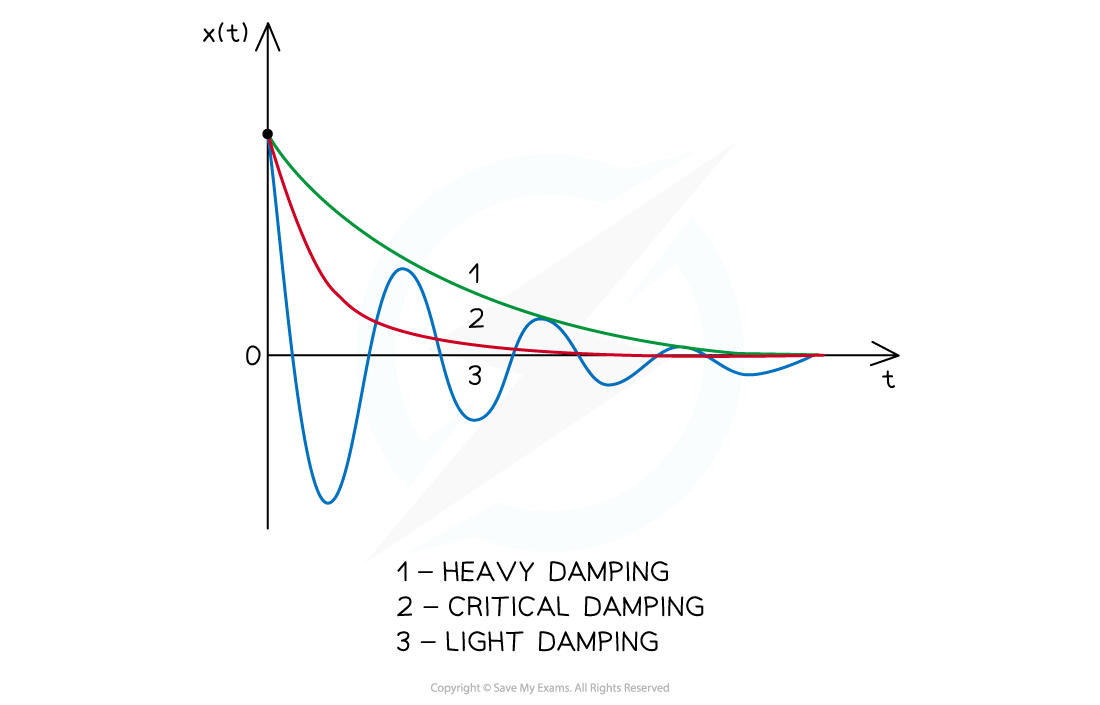
- This is known as heavy damping (sometimes also referred to as overdamping)
- The general solution will be of the form
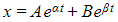 where α and β are the roots
where α and β are the roots 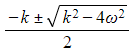 of the auxiliary equation
of the auxiliary equation - Because α and β are both negative, the two exponentials will decay to zero as t increases
- Therefore the particle’s displacement will also decay to zero, without any oscillations occurring
- However the decay to zero will not happen as quickly as in Case 2 (critical damping) below
- CASE 1:
-
- CASE 2:
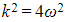
- The auxiliary equation has a single repeated root, which is negative
- This is known as critical damping
- The general solution will be of the form
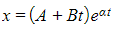 where
where 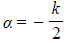 is the repeated root of the auxiliary equation
is the repeated root of the auxiliary equation - Because α is negative, the exponential will decay to zero as t increases
- Therefore the particle’s displacement will also decay to zero, without any oscillations occurring (although depending on the values of A and B it is possible that the particle will change direction once as the decay to zero occurs
- For a given value of
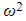 , the displacement of the critical damping case will decay to zero faster than any instance of the heavy damping case
, the displacement of the critical damping case will decay to zero faster than any instance of the heavy damping case
- CASE 3:
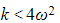
- The auxiliary equation has complex roots which form a complex conjugate pair
- This known as light damping (sometimes also referred to as underdamping)
- The general solution will be of the form
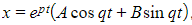 , where
, where 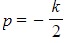 and
and 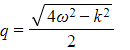
- Because p is negative, the exponential will decay to zero as t increases
- Therefore the particle’s displacement will also decay to zero
- However the cosine and sine terms mean that the particle will continue to oscillate with decreasing amplitude as the decay to zero occurs
- In all three cases, initial or boundary conditions given in a question may allow you to work out the precise values of the arbitrary constants A and B
- CASE 2:
- The following displacement-time graph illustrates the behaviour displayed by a particle for each of the three cases
What is forced harmonic motion?
- If we add a term representing an external ‘driving’ force to the damped harmonic motion equation, the new equation describes a particle undergoing forced harmonic motion
- The standard forced harmonic motion equation is of the form
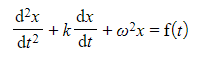
-
- Note that it is the same as the damped harmonic motion equation, except for the addition of the driving term f(t) on the right-hand side of the equation
- x is the displacement of the particle from a fixed point O at time t
- k is a non-negative constant representing the strength of the damping force
- If k = 0 then there is no damping force
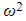 is a positive constant representing the strength of the restoring force that accelerates the particle back towards point O
is a positive constant representing the strength of the restoring force that accelerates the particle back towards point O
- The forced harmonic motion equation is a second order non-homogeneous differential equation, and may be solved using the standard methods for such equations
- This will involve using the auxiliary equation to find the complementary function for the equation
- It will also involve finding the particular integral for the equation, based on the form of f(t)
- Initial or boundary conditions given in a question may allow you to work out the precise values of any arbitrary constants in your general solution
- If k ≠ 0 then the long-term behaviour of the system will be predominantly determined by the driving force f(t)
- If k = 0, then the long-term behaviour will be a combination of the effects of the driving force and of the system’s natural oscillation
Exam Tip
- Even though you may have memorised the forms of the solutions for the damped harmonic motion equation, it is important on an exam question to derive the solution ‘from scratch’, showing your method and working
Worked Example
A particle is moving along a straight line. At time ![]() seconds its displacement
seconds its displacement ![]() metres from a fixed point
metres from a fixed point ![]() is such that
is such that ![]() . At time
. At time ![]() and the velocity of the particle is 3 ms-1.
and the velocity of the particle is 3 ms-1.
(a) Given that k = 10, find an expression for the displacement of the particle at time 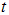 seconds and describe the type of damping that is present.
seconds and describe the type of damping that is present.

(b) Given that 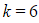 , find an expression for the displacement of the particle at time
, find an expression for the displacement of the particle at time 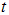 seconds and describe the type of damping that is present.
seconds and describe the type of damping that is present.

(c) Given that k = 4, find an expression for the displacement of the particle at time t seconds and describe the type of damping that is present.
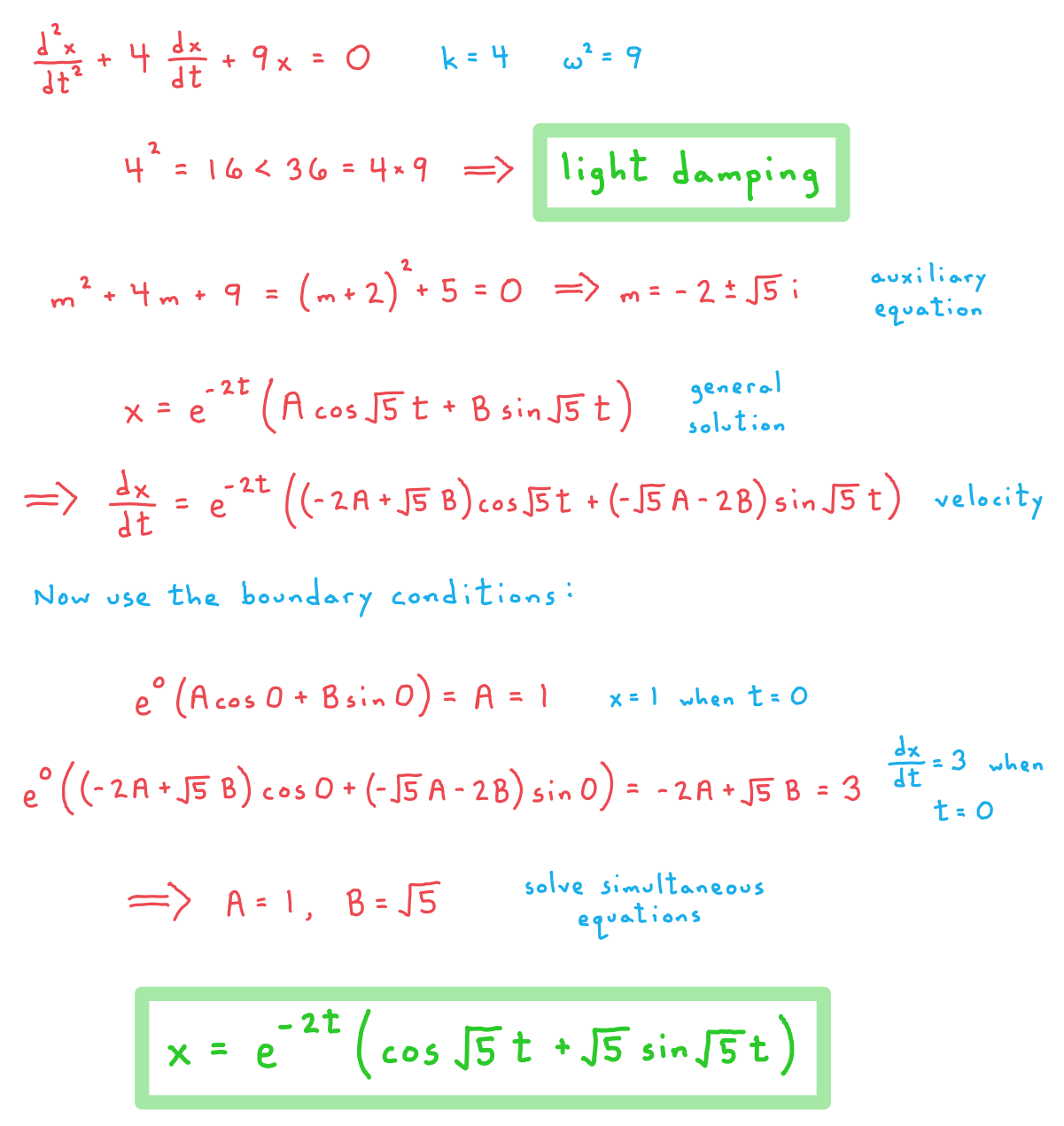
The system is now modified so that at time t seconds the particle’s displacement x metres from the fixed point O is such that . At time t = 0, x = 1 and the velocity of the particle is 3 ms-1.
(d) Find an expression for the displacement of the particle at time t seconds and describe the long-term behaviour of the system.

转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





