- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Further Maths: Core Pure:复习笔记8.3.1 Simple Harmonic Motion
Simple Harmonic Motion (SHM) Equations
What is simple harmonic motion?
- A particle undergoing simple harmonic motion moves along a straight line subject to the following constraints:
- The acceleration of the particle is always directed towards a fixed point on the line of motion
- The acceleration is proportional to the displacement of the particle from the fixed point
- As a result the particle oscillates back and forth along the line around the fixed point
- Many physical systems can be modelled using simple harmonic motion
- One example is an object attached to a spring oscillating in one dimension, when friction, air resistance and other such resistive forces are disregarded
What is the equation that describes simple harmonic motion?
- The standard form of the simple harmonic motion equation is
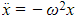
- x is the displacement of the particle from the fixed point
- The fixed point is normally indicated by O and is the origin (i.e. zero point) of the coordinate system
- The fixed point O is known as the centre of oscillation
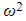 is the constant of proportionality, and represents the strength of the force accelerating the particle back towards point O
is the constant of proportionality, and represents the strength of the force accelerating the particle back towards point O
- The negative sign means that the acceleration is always directed back towards O
- We use
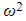 to assure that the constant is positive, and also to simplify the notation for the solution to the equation
to assure that the constant is positive, and also to simplify the notation for the solution to the equation
-
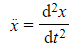 is the acceleration of the particle
is the acceleration of the particle
- With simple harmonic motion, Newton’s ‘dot notation’ is often used for the derivatives
- In this notation, and
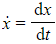
- x is the displacement of the particle from the fixed point
Solutions to SHM Equations
What is the solution to the standard simple harmonic motion equation?
- The SHM equation may be solved using the standard techniques for second order differential equations
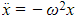 may be rearranged to give the homogeneous second order equation
may be rearranged to give the homogeneous second order equation 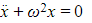
- That has auxiliary equation
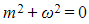 with roots
with roots 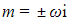
- Therefore the general solution is
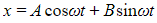
- Initial or boundary conditions given with a question may allow you to find the precise values of the arbitrary constants A and B
- The linear combination of sine and cosine terms in the general solution may be rewritten in the form
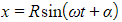
- This can sometimes be a more useful form for the general solution
- This form of the equation shows that the particle oscillates around the fixed point O (i.e., around the centre of oscillation)
- The amplitude of the motion is R
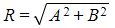
- This is the maximum distance that the particle moves away from the fixed point O
- The period of the motion is
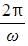
- This is the length of time it takes the particle to complete one oscillation
- The constant α is a ‘phase constant’
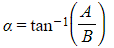
- If α = 0, then the particle is at point O (i.e., x = 0) when t = 0
- If
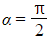 then the particle is at its maximum displacement (i.e., x = R) when t = 0
then the particle is at its maximum displacement (i.e., x = R) when t = 0
How can I solve the simple harmonic motion equation to link displacement x and velocity v?
- Because acceleration is the derivative of velocity, and velocity is the derivative of displacement, we may use the chain rule to write
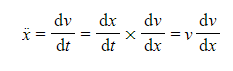
- Substituting that into the standard SHM equation gives
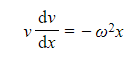
- That form of the SHM equation may be solved using separation of variables:
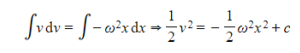
-
- But the velocity is momentarily zero when the particle reaches its maximum displacement
- After this the particle’s velocity changes direction and the particle heads back towards the centre of oscillation
- This gives us a boundary condition (because we know that v = 0 when x = R) and allows us to find the value of the constant of integration:
- But the velocity is momentarily zero when the particle reaches its maximum displacement
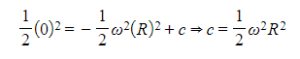
-
- Substituting that value of c into the solution and rearranging gives
![]()
-
-
- where R again is the amplitude of the simple harmonic motion
-
- Note that this version of the solution connects the velocity v to the displacement x, and is independent of the time t
- Taking square roots gives
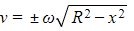
- Be careful when using this to answer questions
- The direction of the velocity (plus or minus) will depend on the displacement (plus or minus) and whether the particle is moving towards or away from the centre of oscillation
- Taking square roots gives
Exam Tip
- Even though you may have memorised the forms of the solutions for the SHM equation, it is important on an exam question to derive the solution ‘from scratch’, showing your method and working
Worked Example
A particle is moving along a straight line. At time t seconds its displacement x metres from a fixed point O is such that 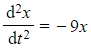 . At time t = 0, x = 2 and the velocity of the particle is 9 ms-1.
. At time t = 0, x = 2 and the velocity of the particle is 9 ms-1.
a) Find an expression for the displacement of the particle at time t seconds.
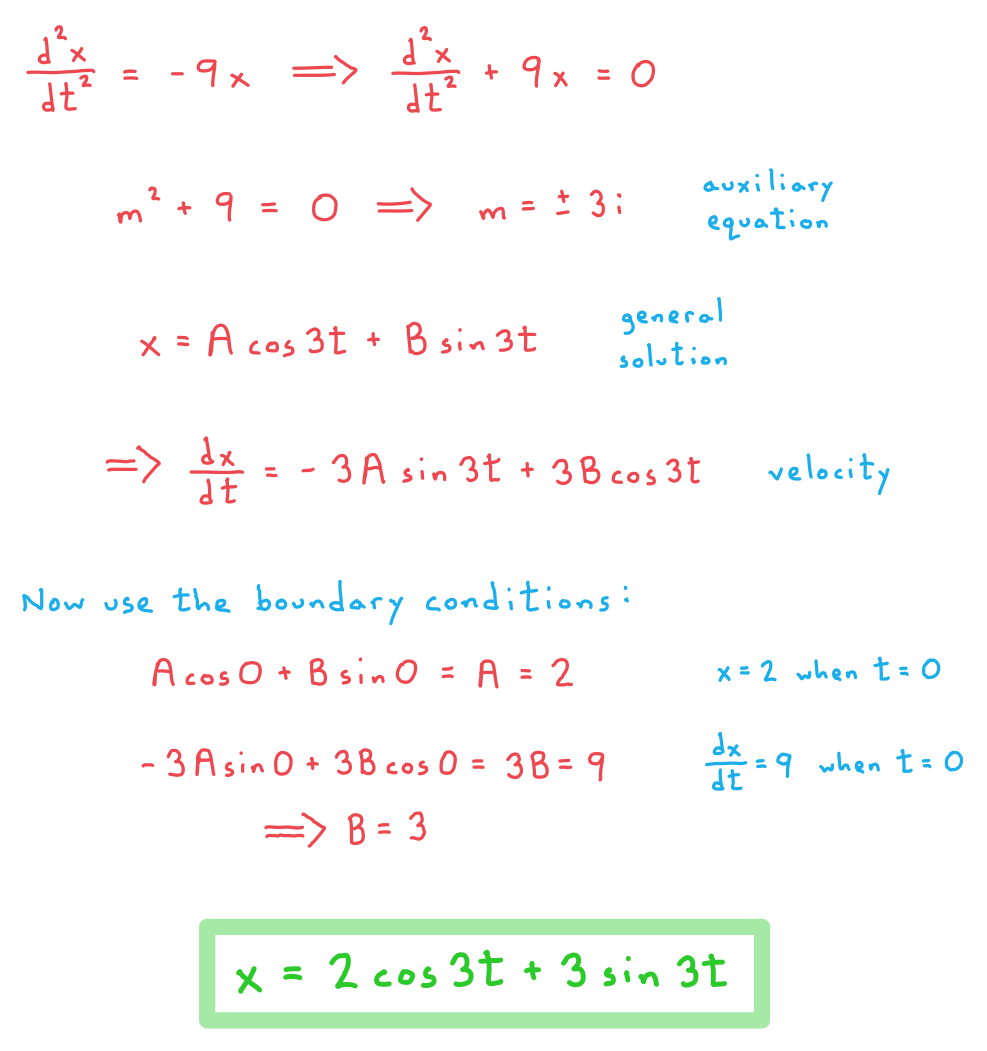
b) Hence determine the maximum displacement of the particle from O.

c) Show that the relationship between the velocity v and displacement x of the particle may be described by the equation 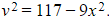 .
.
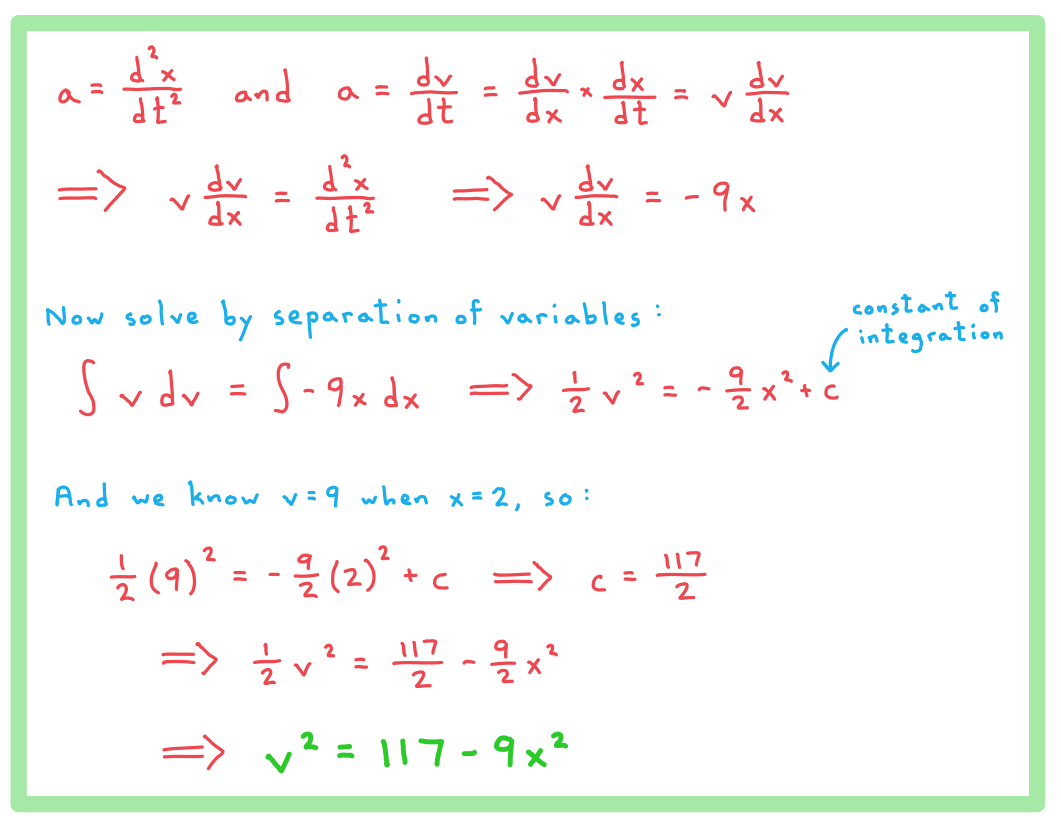
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





