- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Further Maths: Core Pure:复习笔记8.2.1 Solving Second Order Differential Equations
Second Order Differential Equations
What is a second order differential equation?
- A second order differential equation is an equation containing second order derivatives (and possibly first order derivatives) but no higher order derivatives
- For example
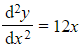 is a second order differential equation
is a second order differential equation - And so is
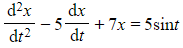
- But
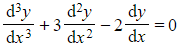 is not, because it contains the third order derivative
is not, because it contains the third order derivative 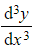
- For example
What are the types of second order differential equation?
- We divide second order differential equations into two main types
- A homogeneous second order differential equation is of the form
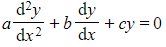 where a, b and c are real constants
where a, b and c are real constants
- You may also see this written in the form
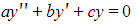 where
where 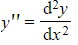 and
and 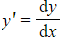
- You may also see this written in the form
- A non-homogeneous second order differential equation is of the form
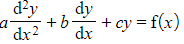 where a, b and c are real constants and where f(x) is a non-zero function of x
where a, b and c are real constants and where f(x) is a non-zero function of x
- You may also see this written in the form
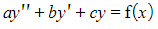
- You may also see this written in the form
How can I solve simple second order differential equations?
- If a second order differential equation is of the form
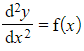 , it will often be possible to solve it simply by using repeated integration
, it will often be possible to solve it simply by using repeated integration
- A separate integration constant will need to be included for each of the integrations
- This means you will end up with two integration constants in your final answer
- To find the values of these constants you will need two separate initial or boundary conditions
- See the worked example below for examples of this
- A separate integration constant will need to be included for each of the integrations
Worked Example
a) Find the general solution to the second order differential equation 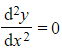 .
.
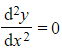 .
.
b) Find the particular solution to the second order differential equation 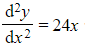 that satisfies
that satisfies 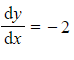 and
and 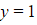 when
when 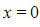 .
.
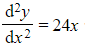 that satisfies
that satisfies 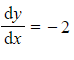 and
and 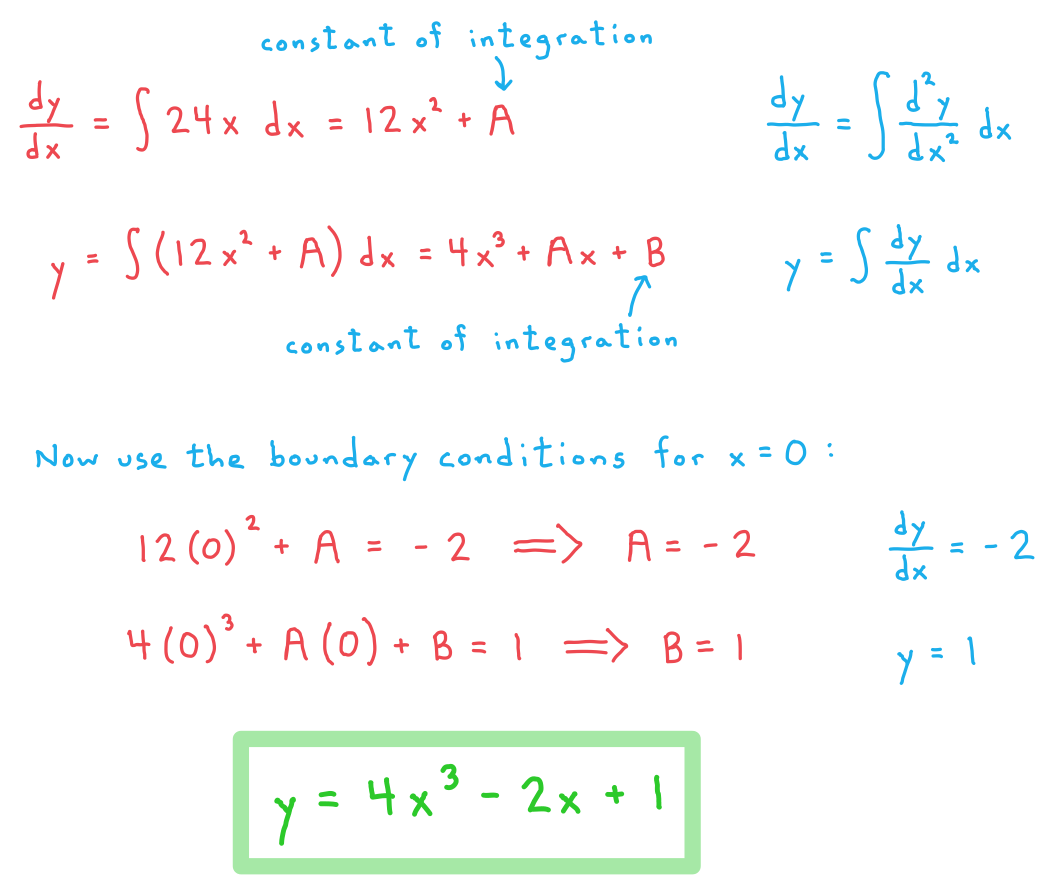
Auxiliary Equations & Complementary Functions
What is a complementary function?
- For a second order homogeneous differential equation, the equation’s complementary function is the general solution to the equation
- If the differential equation contains initial or boundary conditions you may then use those to find the precise solution to the equation
- For a second order non-homogeneous differential equation, the equation’s complementary function is only a part of the general solution to the equation
- For the complete general solution you will need to include the particular integral as well (see the following section)
- In order to find a differential equation’s complementary function we use the associated auxiliary equation
What is an auxiliary equation?
- For a second order differential equation
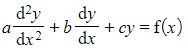 the associated auxiliary equation is
the associated auxiliary equation is 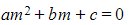
- It is possible that f(x)=0, in which case the differential equation is homogeneous
- The auxiliary equation is exactly the same whether the differential equation is homogeneous or non-homogeneous
- The auxiliary equation is a quadratic equation in the variable m
- The solutions to the auxiliary equation will determine the nature of the associated complementary function
How do I use the auxiliary equation to find the associated complementary function?
- STEP 1: Solve the auxiliary equation
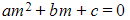 to find its roots α and β
to find its roots α and β
- It is possible that the roots will be repeated, with α = β
- STEP 2: The complementary function will be determined by the nature of the roots of the auxiliary equation:
- CASE 1:
 so that α and β are distinct real roots
so that α and β are distinct real roots
- The complementary function is
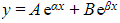 where A and B are arbitrary constants
where A and B are arbitrary constants - This holds even if one of the roots is zero – but if β = 0, say, then the complementary function will become
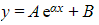
- The complementary function is
- CASE 2:
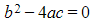 so that there is only one repeated root α
so that there is only one repeated root α
- The complementary function is
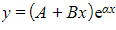 where A and B are arbitrary constants
where A and B are arbitrary constants
- The complementary function is
- CASE 3:
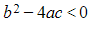 so that α and β are complex conjugate roots that may be written as
so that α and β are complex conjugate roots that may be written as 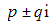
- The complementary function is
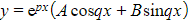 where A and B are arbitrary constants
where A and B are arbitrary constants - Note that if α and β are purely imaginary, then p = 0 and the complementary function becomes
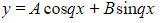
- The complementary function is
- CASE 1:
How do I solve a second order homogeneous differential equation?
- STEPS 1 & 2: Use the auxiliary equation to find the differential equation’s complementary function (see above)
- The complementary function, with its arbitrary constants A and B, is the general solution to the differential equation
- STEP 3: If there are initial or boundary conditions associated with the differential equation, use these to find the values of the general solution’s arbitrary constants
- This gives the particular solution to the differential equation with the given initial or boundary conditions
- Note that because there are two arbitrary constants, you will require two separate initial or boundary conditions to find both constants’ values
- If the initial or boundary conditions involve
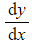 you will need to differentiate your general solution to find
you will need to differentiate your general solution to find 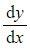 in terms of the constants A and B
in terms of the constants A and B - Finding the values of A and B may require solving simultaneous equations
Worked Example
a) Find the general solution to each of the following differential equations:
(i)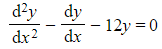
(ii)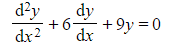
(iii)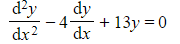

b) For each of the differential equations in part (a), find the particular solution that satisfies 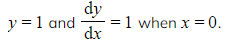

Particular Integral
What is a particular integral?
- A particular integral is part of the solution to a second order non-homogeneous differential equation of the form
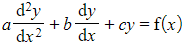
- When the particular integral is substituted into the left hand side it will produce f(x)
- The other part of the solution is the complementary function associated with the differential equation
How do I find the particular integral for a second order non-homogeneous differential equation?
- STEP 1: Choose the correct ‘test form’ of particular integral, based on the function f(x) on the right-hand side of the non-homogeneous differential equation:
| Form of f(x) | ‘Test form’ of p.i | Notes |
| p | λ | p is a given constant λ is a constant to be found |
| p + qx | λ + μx | p & q are given constants λ & μ are constants to be found Use the full test form of the p.i., even if there is no constant term (i.e., even if p = 0) |
| p + qx + rx2 | λ + μx + νx2 | p, q & r are given constants λ, μ & ν are constants to be found Use the full test form of the p.i., even if there is no constant or x term (i.e., even if p = 0 and/or q =0) |
| pekx | λekx | k & p are given constants λ is a constant to be found |
| p cos ωx + q sin ωx | λ cos ωx + μ sin ωx | p, q & ω are given constants λ & μ are constants to be found Use the full test form of the p.i., even if f(x) only contains sin or only contains cos (i.e., even if p = 0 or q =0) |
-
- If all or part of the ‘test form’ of the particular integral occurs in the differential equation’s complementary function, you will need to modify the ‘test form’
- See the following section for how to do this
- STEP 2: Find the first and second derivatives of the ‘test form’ of particular integral
- STEP 3: Substitute the first and second derivatives, along with the ‘test form’ itself, into the differential equation
- STEP 4: By comparing coefficients, determine the correct values to use for the constants in the ‘test form’
- This may require solving simultaneous equations involving the various constants
- The ‘test form’ with the correct values of its constants is the particular integral for the differential equation
What if a part of the ‘test form’ of the particular integral already occurs in the differential equation’ complementary function?
- Because the terms of the complementary function are solutions to the homogeneous equation
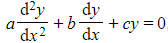 , they cannot also provide possible solutions to the non-homogeneous equation
, they cannot also provide possible solutions to the non-homogeneous equation 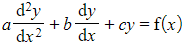
- If the standard ‘test form’ for the particular integral contains terms that already occur as a part of the complementary function, then the ‘test form’ needs to be modified by adding a factor of x (or possibly of powers of x) to the terms of the ‘test form’
- Some examples:
- The equation
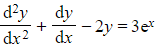 has complementary function
has complementary function
- The standard ‘test form’ of p.i. would be λex, but ex times a constant already occurs in the complementary function
- Therefore
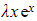 would be used as the ‘test form’ instead
would be used as the ‘test form’ instead
- The equation
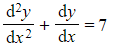 has complementary function
has complementary function 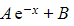
- The standard ‘test form’ of p.i. would be λ, but a constant (B) already occurs in the complementary function
- Therefore
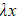 would be used as the ‘test form’ instead
would be used as the ‘test form’ instead
- The equation
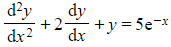 has complementary function
has complementary function 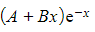
- The standard ‘test form’ of p.i. would be λe-x, but e-xtimes a constant AND xe-xtimes a constant both already occur in the complementary function
- Therefore
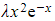 would be used as the ‘test form’ instead
would be used as the ‘test form’ instead
- The equation
How do I solve a second order non-homogeneous differential equation?
- STEP 1: Use the auxiliary equation to find the differential equation’s complementary function (‘c.f.’)
- STEP 2: Find the differential equation’s particular integral (‘p.i.’) including the correct values of any constants
- STEP 3: The general solution to the differential equation is the sum of the complementary function and the particular integral
- I.e., the general solution is y = c.f. + p.i.
- STEP 4: If there are initial or boundary conditions associated with the differential equation, use these to find the values of the general solution’s arbitrary constants
- This gives the particular solution to the differential equation with the given initial or boundary conditions
- Note that because there are two arbitrary constants (A and B from the complementary function), you will require two separate initial or boundary conditions to find both constants’ values
- If the initial or boundary conditions involve
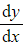 you will need to differentiate your general solution to find
you will need to differentiate your general solution to find 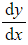 in terms of the constants A and B
in terms of the constants A and B - Finding the values of A and B may require solving simultaneous equations
Exam Tip
- Don’t forget to include the complementary function in your solution to a second order non-homogeneous differential equation – the solution is incomplete without it!
- If your attempt to find the constants for a particular integral breaks down and doesn’t appear to have a solution, make sure that you have not used a ‘test form’ of the p.i. that includes terms also found in the complementary function
- Finding the constants for the particular integral can be a very fiddly and algebra-heavy process – be sure to work slowly and methodically to avoid mistakes!
Worked Example
a) Find the general solution to the differential equation 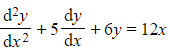 .
.
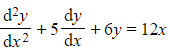 .
.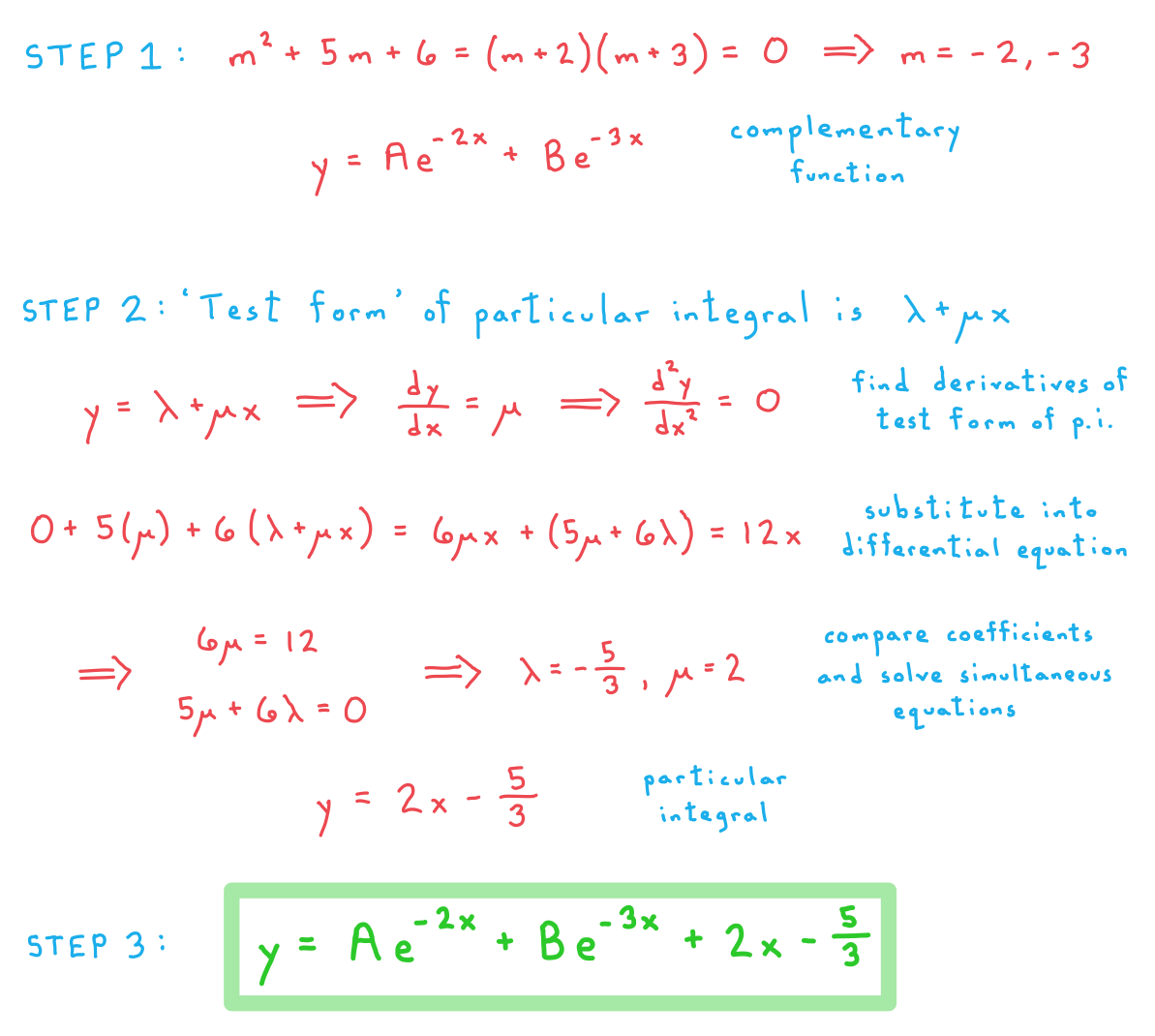
b) Find the general solution to the differential equation 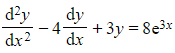 .
.
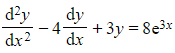 .
.
c) Find the particular solution to the differential equation 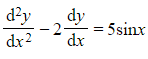 that satisfies
that satisfies 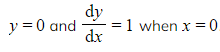 .
.
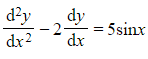 that satisfies
that satisfies 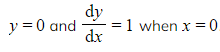 .
.
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





