- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Further Maths: Core Pure:复习笔记8.1.2 Solving First Order Differential Equations
First Order Differential Equations
What is a differential equation?
- A differential equation is simply an equation that contains derivatives
- For example
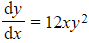 is a differential equation
is a differential equation - And so is
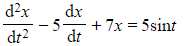
- For example
What is a first order differential equation?
- A first order differential equation is a differential equation that contains first derivatives but no second (or higher) derivatives
- For example
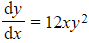 is a first order differential equation
is a first order differential equation - But
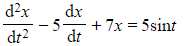 is not a first order differential equation, because it contains the second derivative
is not a first order differential equation, because it contains the second derivative 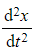
- For example
- The general solution to a first order differential equation will have one unknown constant
- To find the particular solution you will need to know an initial condition or a boundary condition
Wait – haven’t I seen first order differential equations before?
- Yes you have!
- For example
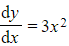 is also a first order differential equation, because it contains a first derivative and no second (or higher) derivatives
is also a first order differential equation, because it contains a first derivative and no second (or higher) derivatives - But for that equation you can just integrate to find the solution y = x3 + c (where c is a constant of integration)
- For example
- In A Level Maths you will have solved some first order differential equations using the method of separation of variables
Integrating Factors
What is an integrating factor?
- An integrating factor can be used to solve a differential equation that can be written in the standard form
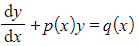
- Be careful – the ‘functions of x’ p(x) and q(x) may just be constants!
- For example in
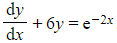 , p(x) = 6 and q(x) = e-2x
, p(x) = 6 and q(x) = e-2x - While in
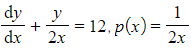 and q(x) = 12
and q(x) = 12
- For example in
- Be careful – the ‘functions of x’ p(x) and q(x) may just be constants!
- For an equation in standard form, the integrating factor is
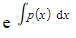
How do I use an integrating factor to solve a differential equation?
- STEP 1: If necessary, rearrange the differential equation into standard form
- STEP 2: Find the integrating factor
- Note that you don’t need to include a constant of integration here when you integrate ∫p(x) dx
- STEP 3: Multiply both sides of the differential equation by the integrating factor
- This will turn the equation into an exact differential equation of the form
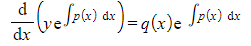
- STEP 4: Integrate both sides of the equation with respect to x
- The left side will automatically integrate to
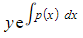
- For the right side, integrate
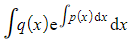 using your usual techniques for integration
using your usual techniques for integration - Don’t forget to include a constant of integration
- Although there are two integrals, you only need to include one constant of integration
- The left side will automatically integrate to
- STEP 5: Rearrange your solution to get it in the form y = f(x)
What else should I know about using an integrating factor to solve differential equations?
- After finding the general solution using the steps above you may be asked to do other things with the solution
- For example you may be asked to find the solution corresponding to certain initial or boundary conditions
Worked Example
Consider the differential equation 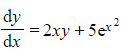 where y = 7 when x = 0.
where y = 7 when x = 0.
Use an integrating factor to find the solution to the differential equation with the given boundary condition.

转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





