- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Further Maths: Core Pure:复习笔记6.2.4 Shortest Distances - Planes
Shortest Distance between a Point & a Plane
How do I find the shortest distance between a given point on a line and a plane?
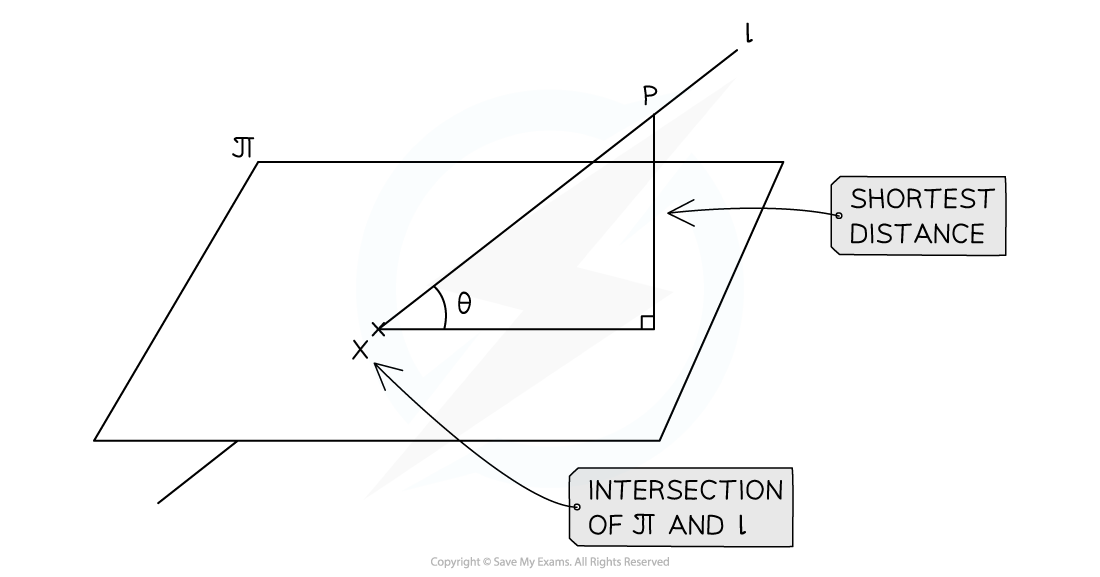
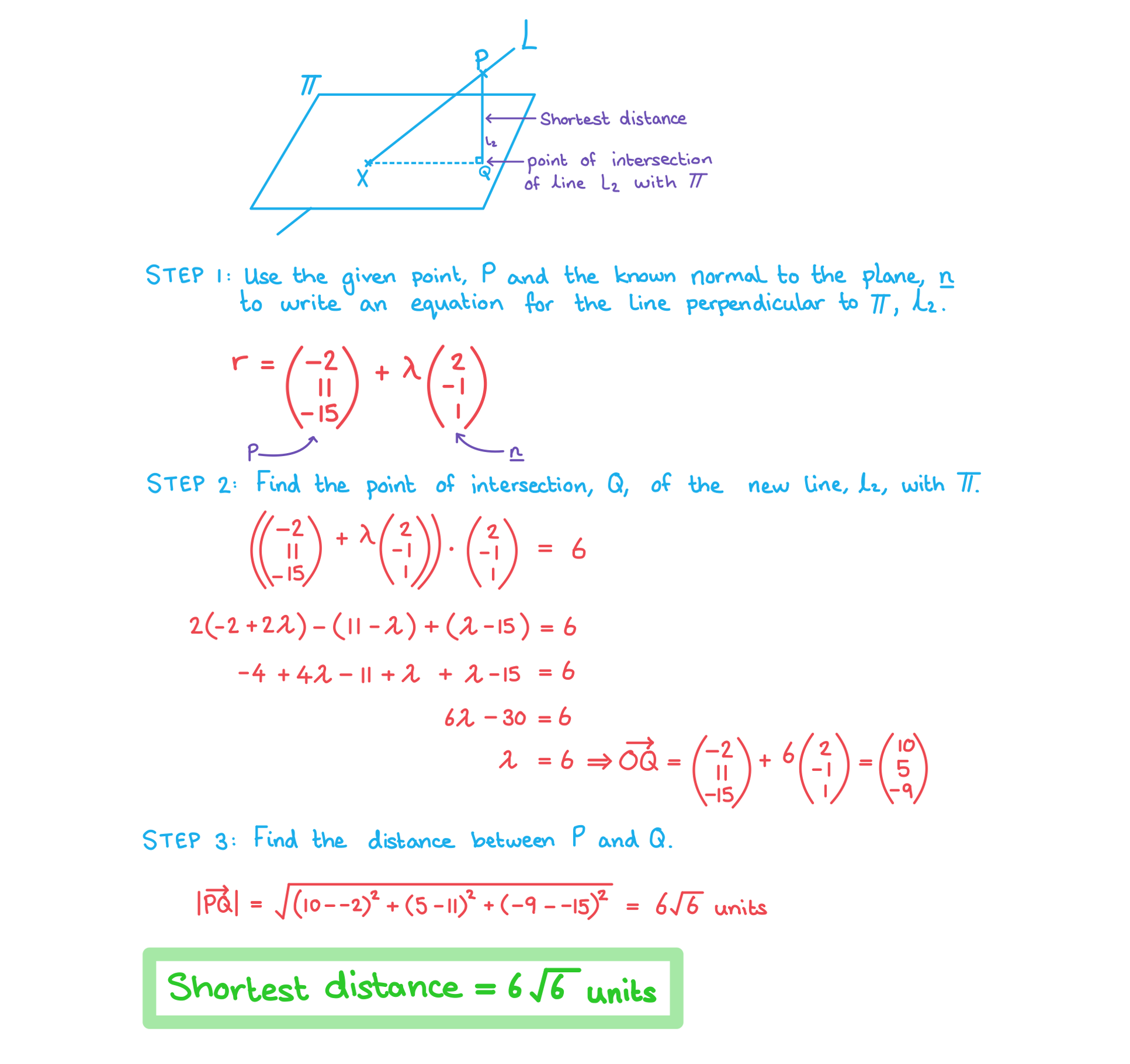
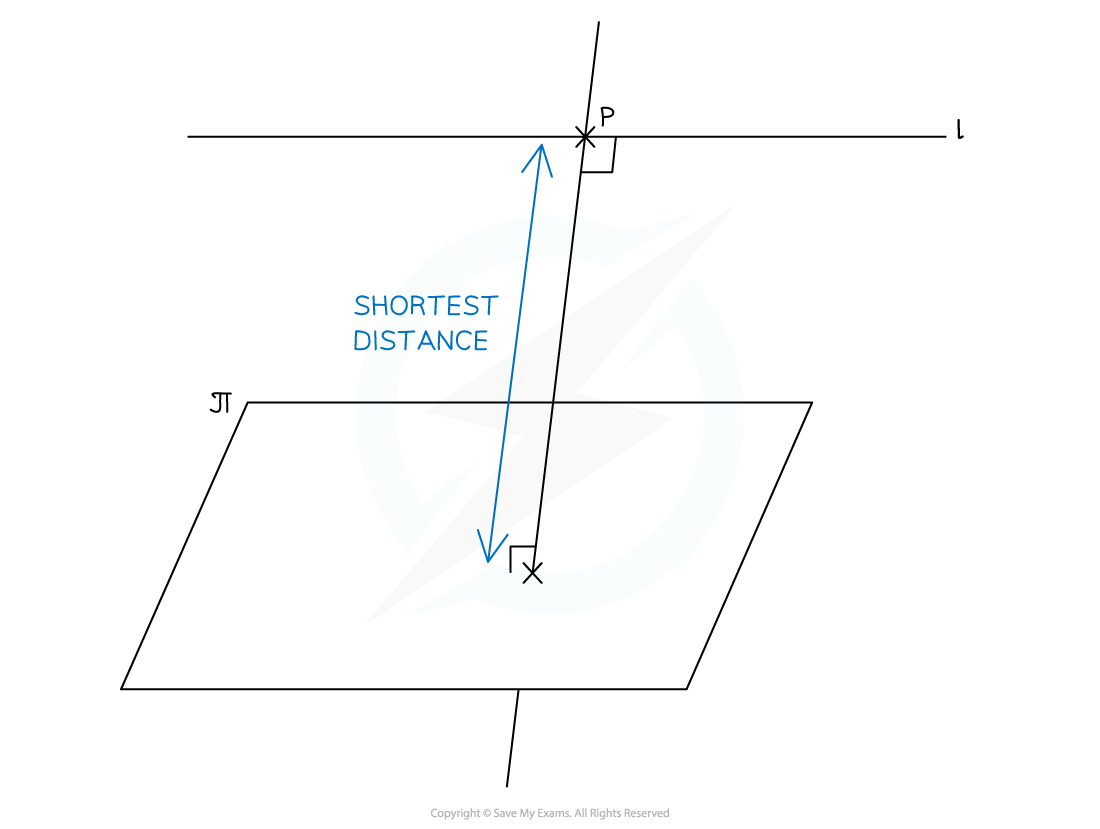
- The shortest distance from any point on a line to a plane will always be the perpendicular distance from the point to the plane
- Given a point, P, on the line
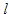 with equation
with equation 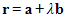 and a plane
and a plane 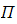 with equation
with equation 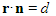
- STEP 1: Find the vector equation of the line perpendicular to the plane that goes through the point, P, on
- This will have the position vector of the point, P, and the direction vector n
- STEP 2: Find the coordinates of the point of intersection of this new line with
 by substituting the equation of the line into the equation of the plane
by substituting the equation of the line into the equation of the plane - STEP 3: Find the distance between the given point on the line and the point of intersection
- This will be the shortest distance from the plane to the point
- STEP 1: Find the vector equation of the line perpendicular to the plane that goes through the point, P, on
- A question may provide the acute angle between the line and the plane
- Use right-angled trigonometry to find the perpendicular distance between the point on the line and the plane
- Drawing a clear diagram will help
- Use right-angled trigonometry to find the perpendicular distance between the point on the line and the plane
Worked Example
The plane ![]() has equation
has equation 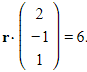 .
.
The line ![]() has equation
has equation 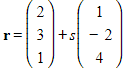 .
.
The point ![]() lies on the line
lies on the line ![]() .
.
Find the shortest distance between the point P and the plane ![]() .
.
Shortest Distance between a Line & a Plane
How do I find the shortest distance between a plane and a line parallel to the plane?
- The shortest distance between a line and a plane that are parallel to each other will be the perpendicular distance from the line to the plane
- Given a line
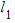 with equation
with equation 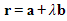 and a plane
and a plane 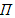 parallel to
parallel to 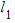 with equation
with equation 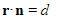
- Where n is the normal vector to the plane
- STEP 1: Find the equation of the line
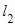 perpendicular to
perpendicular to 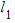 and
and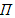 going through the point a in the form
going through the point a in the form 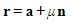
- STEP 2: Find the point of intersection of the line
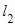 and
and
- STEP 3: Find the distance between the point of intersection and the point,
Shortest Distance between two Planes
How do I find the shortest distance between two parallel planes?
- Two parallel planes will never intersect
- The shortest distance between two parallel planes will be the perpendicular distance between them
- Given a plane
 with equation
with equation 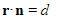 and a plane
and a plane 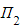 with equation
with equation 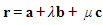 then the shortest distance between them can be found
then the shortest distance between them can be found
- STEP 1: The equation of the line perpendicular to both planes and through the point a can be written in the form r = a + sn
- STEP 2: Substitute the equation of the line into
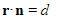 to find the coordinates of the point where the line meets
to find the coordinates of the point where the line meets 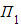
- STEP 3: Find the distance between the two points of intersection of the line with the two planes
Consider the parallel planes defined by the equations:
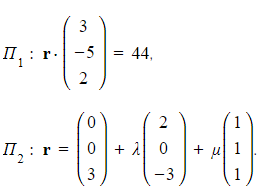 ,
,
.
a) Show that the two planes 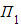 and
and 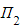 are parallel.
are parallel.

b) Find the shortest distance between the two planes 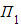 and
and 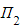 .
.

转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





