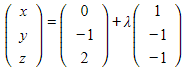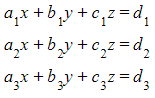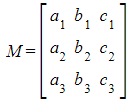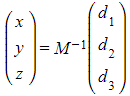- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Further Maths: Core Pure:复习笔记6.2.3 Combinations of Planes
Intersection of Planes
How do we find the line of intersection of two planes?
- Two planes will either be parallel or they will intersect along a line
- Consider the point where a wall meets a floor or a ceiling
- You will need to find the equation of the line of intersection
- If you have the Cartesian forms of the two planes then the equation of the line of intersection can be found by solving the two equations simultaneously
- As the solution is a vector equation of a line rather than a unique point you will see below how the equation of the line can be found by part solving the equations
- For example:
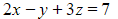 (1)
(1)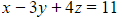 (2)
(2)
- STEP 1: Choose one variable and substitute this variable for λ in both equations
- For example, letting x = λ gives:
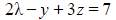 (1)
(1)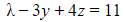 (2)
(2)
- For example, letting x = λ gives:
- STEP 2: Rearrange the two equations to bring λ to one side
- Equations (1) and (2) become
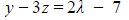 (1)
(1)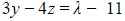 (2)
(2)
- Equations (1) and (2) become
- STEP 3: Solve the equations simultaneously to find the two variables in terms of λ
- 3(1) – (2) Gives
- Substituting this into (1) gives
- 3(1) – (2) Gives
- STEP 4: Write the three parametric equations for x, y, and z in terms of λ and convert into the vector equation of a line in the form
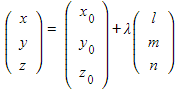
- The parametric equations
- Become
- The parametric equations
- If you have fractions in your direction vector you can change its magnitude by multiplying each one by their common denominator
- The magnitude of the direction vector can be changed without changing the equation of a line
- An alternative method is to find two points on both planes by setting either x, y, or z to zero and solving the system of equations using your calculator
- Repeat this twice to get two points on both planes
- These two points can then be used to find the vector equation of the line between them
- This will be the line of intersection of the planes
- This method relies on the line of intersection having points where the chosen variables are equal to zero
Worked Example
Two planes ![]() and
and ![]() are defined by the equations:
are defined by the equations:
![]()
![]()
Find the vector equation of the line of intersection of the two planes.

Angle between two Planes
How do we find the angle between two planes?
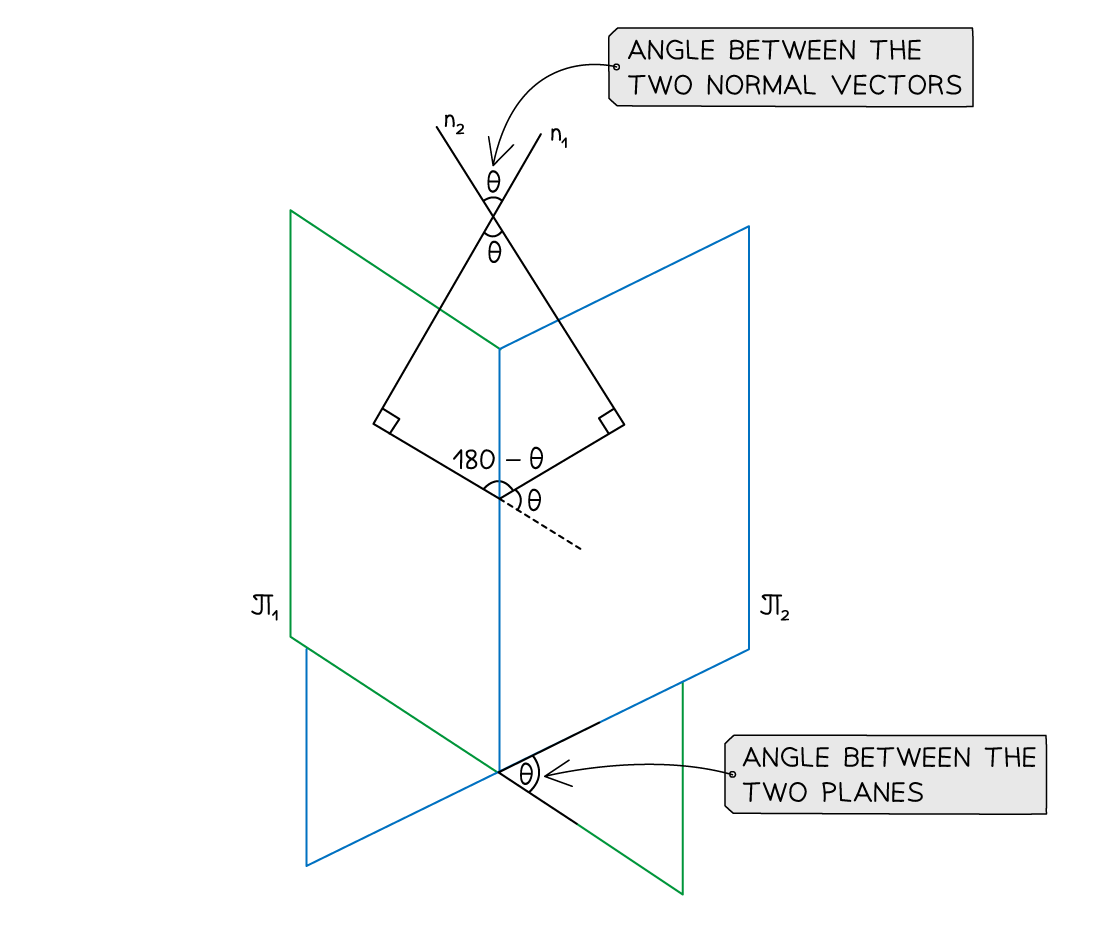
- The angle between two planes is equal to the angle between their normal vectors
- It can be found using the scalar product of their normal vectors
- If two planes Π1 and Π2 with normal vectors n1 and n2 meet at an angle then the two planes and the two normal vectors will form a quadrilateral
- The angles between the planes and the normal will both be 90°
- The angle between the two planes and the angle opposite it (between the two normal vectors) will add up to 180°
Exam Tip
- In your exam read the question carefully to see if you need to find the acute or obtuse angle
- When revising, get into the practice of double checking at the end of a question whether your angle is acute or obtuse and whether this fits the question
Worked Example
Find the acute angle between the two planes which can be defined by equations ![]() and
and ![]() .
.

Combinations of three Planes
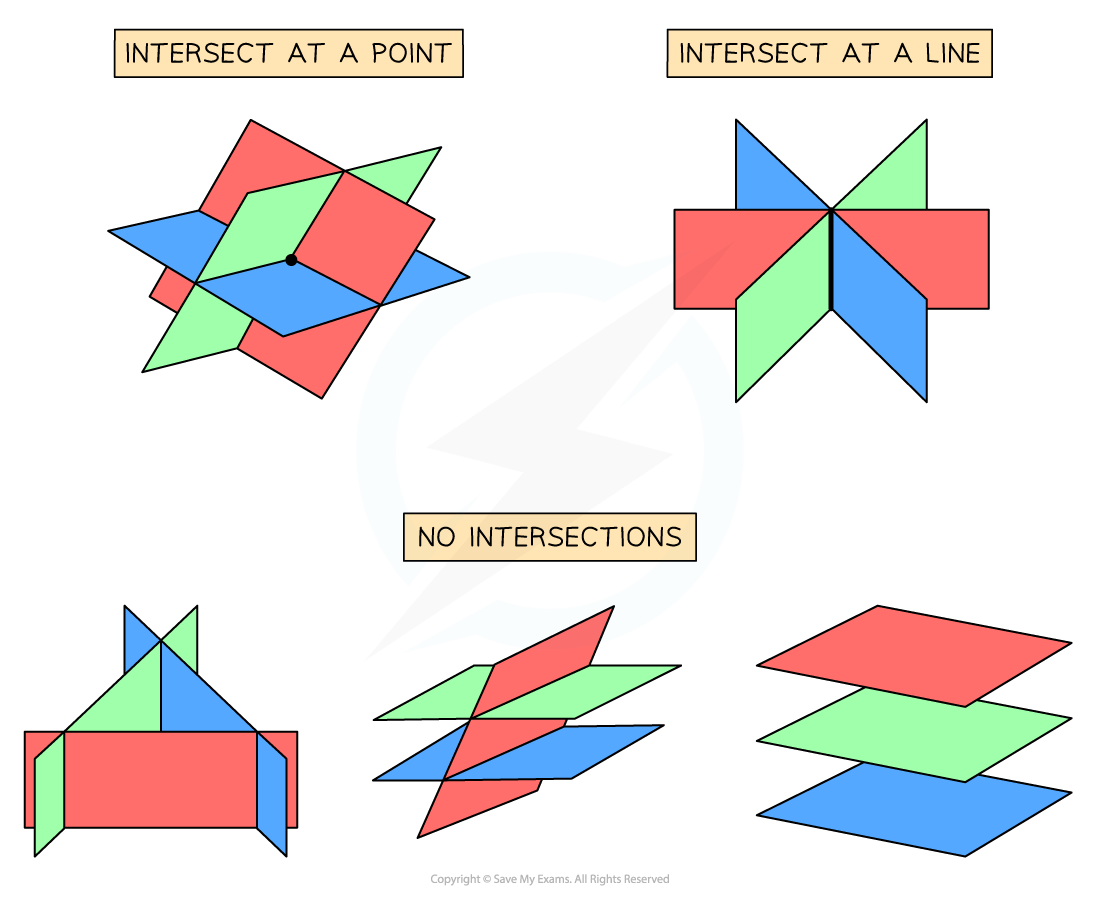
What are the possible configurations of three planes?
- Form three equations using the three planes
- Let the matrix M be equal to the coefficients
- If
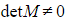 then the three planes intersect at a single point
then the three planes intersect at a single point
- If
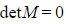 then the three planes could
then the three planes could
- Be the coincident or parallel
- Check if the normal vectors are parallel
- If they are coincident then there will be infinitely many solutions
- If they are parallel then there will be no solutions
- Intersect at a line
- This is configuration is called a sheaf
- Form a triangular prism
- This is where pairs of planes interest at lines which are parallel to each other
- Two could be parallel and the third could interest each plane separately
- Be the coincident or parallel
How can I find the configuration of three planes?
- If the matrix of coefficients is non-singular then the planes intersect at a single point
- If the matrix is singular then check if any of the planes are parallel or coincident
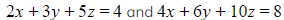 are coincident as they are scalar multiples
are coincident as they are scalar multiples are parallel as their normal vectors are parallel
are parallel as their normal vectors are parallel
- If the planes are not parallel then try to check to see if the equations are consistent
- Consistent equations will have solutions
- Inconsistent equations will not have any solutions
- If the planes are not parallel and the equations are consistent then they form a sheaf
- They intersect at a line
- Eliminating variables will lead to the equation of this line
- Eliminating all variables will lead to a statement that is always true
- Such as 0 = 0
- If the planes are not parallel and the equations are inconsistent then they form a triangular prism
- They do not intersect
- Each pair of planes intersect a line and these three lines are parallel
- Eliminating all variables will lead to a statement that is never true
- Such as 0 = 1
Worked Example
Three planes have equations given by
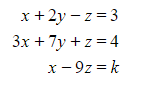
a) Given that the three planes intersect in a straight line, find the value of 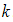 .
.

b) Find a vector equation for the line of intersection.
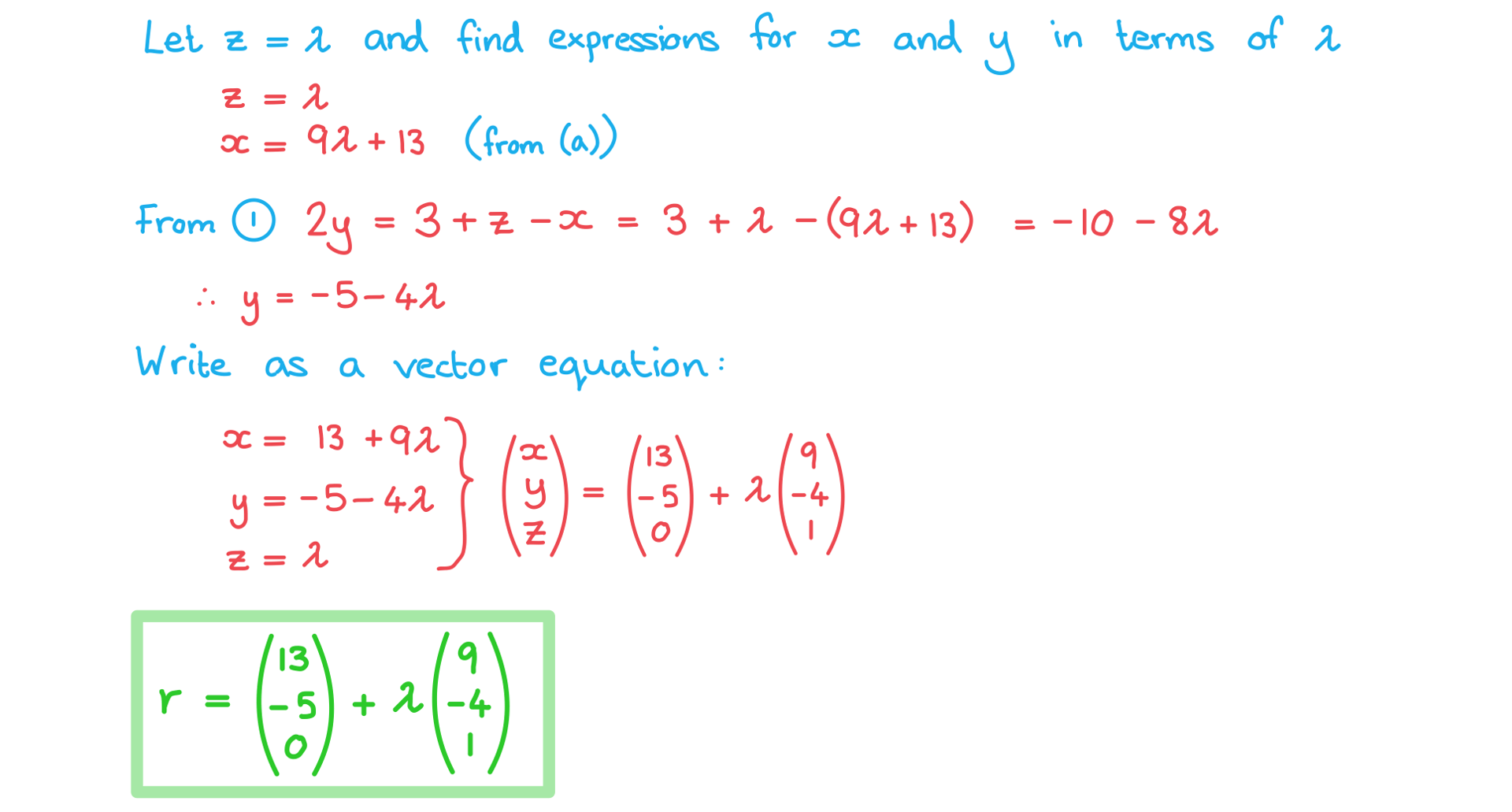
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1