- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Further Maths: Core Pure:复习笔记6.2.1 Equations of planes
Equation of a Plane in Vector Form
How do I find the vector equation of a plane?
- A plane is a flat surface which is two-dimensional
- Imagine a flat piece of paper that continues on forever in both directions
- A plane in often denoted using the capital Greek letter Π
- The vector form of the equation of a plane can be found using two direction vectors on the plane
- The direction vectors must be
- parallel to the plane
- not parallel to each other
- therefore they will intersect at some point on the plane
- The direction vectors must be
- The formula for finding the vector equation of a plane is
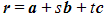
- Where r is the position vector of any point on the plane
- a is the position vector of a known point on the plane
- b and c are two non-parallel direction (displacement) vectors parallel to the plane
- s and t are scalars
- The formula can also be written as
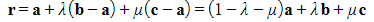
- Where r is the position vector of any point on the plane
- a, b, c are the position vectors of known points on the plane
- λ and μ are scalars
- These formulae are given in the formula booklet but you must make sure you know what each part means
- As a could be the position vector of any point on the plane and b and c could be any non-parallel direction vectors on the plane there are infinite vector equations for a single plane
How do I determine whether a point lies on a plane?
- Given the equation of a plane
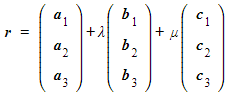 then the point r with position vector
then the point r with position vector 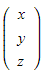 is on the plane if there exists a value of λ and μ such that
is on the plane if there exists a value of λ and μ such that
-
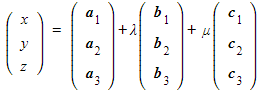
- This means that there exists a single value of λ and μ that satisfy the three parametric equations:
- Solve two of the equations first to find the values of λ and μ that satisfy the first two equation and then check that this value also satisfies the third equation
- If the values of λ and μ do not satisfy all three equations, then the point r does not lie on the plane
Exam Tip
- The formula for the vector equation of a plane is given in the formula booklet, make sure you know what each part means
- Be careful to use different letters, e.g. λ and μ as the scalar multiples of the two direction vectors
Worked Example
The points A, B and C have position vectors ![]() respectively, relative to the origin O.
respectively, relative to the origin O.
(a) Find the vector equation of the plane.

(b) Determine whether the point D with coordinates (-2, -3, 5) lies on the plane.

Equation of a Plane in Cartesian Form
How do I find the vector equation of a plane in cartesian form?
- The cartesian equation of a plane is given in the form
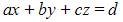
- This is given in the formula booklet
- A normal vector to the plane can be used along with a known point on the plane to find the cartesian equation of the plane
- The normal vector will be a vector that is perpendicular to the plane
- The scalar product of the normal vector and any direction vector on the plane will the zero
- The two vectors will be perpendicular to each other
- The direction vector from a fixed-point A to any point on the plane, R can be written as r – a
- Then n ∙ (r – a) = 0 and it follows that (n ∙ r) – (n ∙ a) = 0
- This gives the equation of a plane using the normal vector:
- n ∙ r = a ∙ n
- Where r is the position vector of any point on the plane
- a is the position vector of a known point on the plane
- n is a vector that is normal to the plane
- This is given in the formula booklet
- n ∙ r = a ∙ n
- If the vector r is given in the form
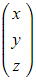 and a and n are both known vectors given in the form
and a and n are both known vectors given in the form 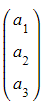 and
and 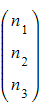 then the Cartesian equation of the plane can be found using:
then the Cartesian equation of the plane can be found using:
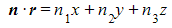
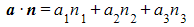
- Therefore
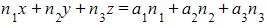
- This simplifies to the form
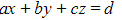
- A version of this is given in the formula booklet
How do I find the equation of a plane in Cartesian form given the vector form?
- Given the equation of the plane
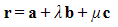
- Form three equations
- Form three equations
- Choose a pair of equations and use them to form an equation without μ
- Choose another pair and form another equation without μ
- Use your two expressions to form an equation without μ and λ
- Rewrite the equation in the form
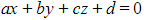
Exam Tip
- In an exam, using whichever form of the equation of the plane to write down a normal vector to the plane is always a good starting point
Worked Example
A plane ![]() has equation
has equation 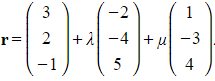 . Find the equation of the plane in its Cartesian form.
. Find the equation of the plane in its Cartesian form.

转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





