- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Further Maths: Core Pure:复习笔记6.1.4 Shortest Distances - Lines
Shortest Distance between a Point & a Line
How do I find the shortest distance from a point to a line?
- The shortest distance from any point to a line will always be the perpendicular distance
- Given a line l with equation
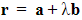 and a point P not on l
and a point P not on l - The scalar product of the direction vector, b, and the vector in the direction of the shortest distance will be zero
- Given a line l with equation
- The shortest distance can be found using the following steps:
- STEP 1: Let the vector equation of the line be r and the point not on the line be P, then the point on the line closest to P will be the point F
- The point F is sometimes called the foot of the perpendicular
- STEP 2: Sketch a diagram showing the line l and the points P and F
- The vector
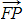 will be perpendicular to the line l
will be perpendicular to the line l
- The vector
- STEP 3: Use the equation of the line to find the position vector of the point F in terms of λ
- STEP 4: Use this to find the displacement vector
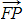 in terms of λ
in terms of λ - STEP 5: The scalar product of the direction vector of the line l and the displacement vector
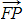 will be zero
will be zero
- Form an equation
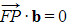 and solve to find λ
and solve to find λ
- Form an equation
- STEP 6: Substitute λ into
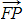 and find the magnitude
and find the magnitude 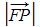
- The shortest distance from the point to the line will be the magnitude of
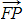
- The shortest distance from the point to the line will be the magnitude of
- STEP 1: Let the vector equation of the line be r and the point not on the line be P, then the point on the line closest to P will be the point F
- Note that the shortest distance between the point and the line is sometimes referred to as the length of the perpendicular

Exam Tip
- Column vectors can be easier and clearer to work with when dealing with scalar products.
Worked Example
Point A has coordinates (1, 2, 0) and the line ![]() has equation
has equation 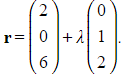 .
.
Find the shortest distance from A to the line ![]() .
.

Shortest Distance between two Lines
How do we find the shortest distance between two parallel lines?
- Two parallel lines will never intersect
- The shortest distance between two parallel lines will be the perpendicular distance between them
- Given a line
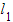 with equation
with equation 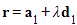 and a line
and a line 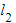 with equation
with equation 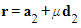 then the shortest distance between them can be found using the following steps:
then the shortest distance between them can be found using the following steps:
- Remember the direction vectors
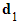 and
and 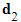 are scalar multiples of each other and so either can be used here
are scalar multiples of each other and so either can be used here - STEP 1: Find the vector between
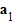 and a general coordinate from
and a general coordinate from 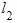 in terms of μ
in terms of μ - STEP 2: Set the scalar product of the vector found in STEP 1 and the direction vector
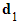 equal to zero
equal to zero - STEP 3: Form and solve an equation to find the value of μ
- STEP 4: Substitute the value of μ back into the equation for
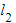 to find the coordinate on
to find the coordinate on 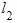 closest to
closest to 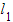
- STEP 5: Find the distance between
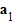 and the coordinate found in STEP 4
and the coordinate found in STEP 4
- Remember the direction vectors
How do we find the shortest distance from a given point on a line to another line?
- The shortest distance from any point on a line to another line will be the perpendicular distance from the point to the line
- If the angle between the two lines is known or can be found then right-angled trigonometry can be used to find the perpendicular distance
- Alternatively, the equation of the line can be used to find a general coordinate and the steps above can be followed to find the shortest distance
How do we find the shortest distance between two skew lines?
- Two skew lines are not parallel but will never intersect
- The shortest distance between two skew lines will be perpendicular to both of the lines
- To find the shortest distance between two skew lines with equations
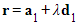 and
and 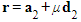 ,
,
- STEP 1: Find position vectors for the points on each line that form the shortest distance
- Point P has position vector
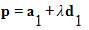
- Point Q has position vector
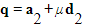
- Point P has position vector
- STEP 2: Find the displacement vector between P and Q
- STEP 3: Form two equations by using the fact that the scalar product of the displacement vector and the direction vector of each line should equal zero
- STEP 4: Solve the two equations simultaneously to find the values of λ and μ
- STEP 5: Substitute the values of λ and μ into the displacement vector and take the magnitude
- Shortest distance =
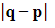
- Shortest distance =
- STEP 1: Find position vectors for the points on each line that form the shortest distance
Exam Tip
- Exam questions will often ask for the shortest, or minimum, distance within vector questions
- If you’re unsure start by sketching a quick diagram
- Sometimes calculus can be used, however usually vector methods are required
Worked Example
Consider the skew lines ![]() and
and ![]() as defined by:
as defined by:
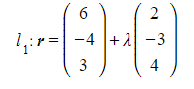
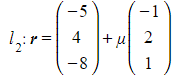
Find the minimum distance between the two lines.

转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





