- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Further Maths: Core Pure:复习笔记6.1.3 Angle between Lines
Scalar Product
The scalar product is an important link between the algebra of vectors and the trigonometry of vectors. We shall see that the scalar product is somewhat comparable to the operation of multiplication on real numbers.
What is the scalar (dot) product?
- The scalar product between two vectors a and b is represented by
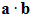
- This is also called the dot product because of the symbol used
- The scalar product between two vectors
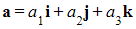 and
and 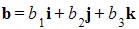 is defined as
is defined as 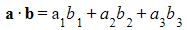
- The result of taking the scalar product of two vectors is a real number
- i.e. a scalar
- For example,
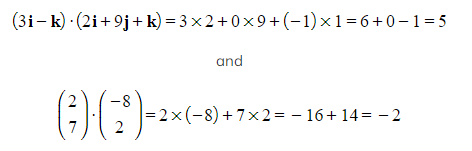
- The scalar product has some important properties:
- The order of the vectors doesn’t affect the result:
![]()
- In effect we can ‘multiply out’ brackets:
![]()
- This means that we can do many of the same things with vectors as we can do when operating on real numbers – for example,
![]()
- The scalar product between a vector and itself is equal to the square of its magnitude:
![]()
For example,
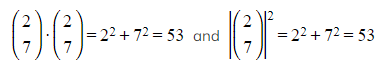
What is the connection between the scalar product and trigonometry?
- There is another important method for finding
 involving the angle between the two vectors θ:
involving the angle between the two vectors θ:
![]()
-
- Here θ is the angle between the vectors when they are placed ‘base to base’
- when the vectors are placed so that they begin at the same point
- This formula can be derived using the cosine rule and expanding
- Here θ is the angle between the vectors when they are placed ‘base to base’
- The scalar product of two vectors gives information about the angle between the two vectors
- If the scalar product is positive then the angle between the two vectors is acute (less than 90°)
- If the scalar product is negative then the angle between the two vectors is obtuse (between 90° and 180°)
- If the scalar product is zero then the angle between the two vectors is 90° (the two vectors are perpendicular)

How do I tell if vectors or lines are perpendicular?
- Two (non-zero) vectors a and b are perpendicular if, and only if,
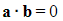
- If the a and b are perpendicular then:
- If
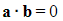 then:
then:
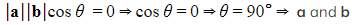 are perpendicular
are perpendicular
- For example, the vectors
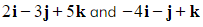 are perpendicular since
are perpendicular since
- If the a and b are perpendicular then:
![]()
Exam Tip
- When writing a scalar product, it’s important to write a distinctive dot between the vectors – otherwise your meaning will not be clear.
Worked Example
Find the value of t such that the two vectors 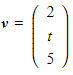 and
and ![]() are perpendicular to each other.
are perpendicular to each other.

Angle between Lines
How do I find the angle between two vectors?
- Recall that a formula for the scalar (or ‘dot’) between vectors a and b is
![]()
-
- where θ is the angle between the vectors when they are placed ‘base to base’
- that is, when the vectors are positioned so that they start at the same point
- We arrange this formula to make
 the subject:
the subject: - To find the angle between two vectors
- Calculate the scalar product between them
- Calculate the magnitude of each vector
- Use the formula to find

- Use inverse trig to find θ
- where θ is the angle between the vectors when they are placed ‘base to base’
How do I find the angle between two lines?
- To find the angle between two lines, find the angle between their direction vectors
-
- For example, if the lines have equations
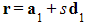 and
and 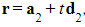 , then the angle θ between the lines is given by
, then the angle θ between the lines is given by
- For example, if the lines have equations
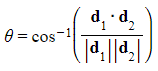
Worked Example
Calculate the angle formed by the two vectors 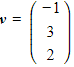 and
and ![]() .
.

转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





