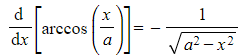- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Further Maths: Core Pure:复习笔记5.2.5 Integration by Substitution
Integrating using Trigonometric Substitutions
The integrals covered in this revision note are based on the standard results
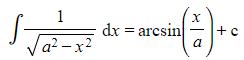
and
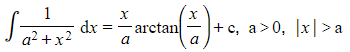
These are given in the formulae booklet
How do I know when to use a trigonometric substitution in integration?
There are three main types of problem
- Type 1
Showing the standard results using a substitution (α may have a value)
The substitution will not be given in such cases
e.g. Use a suitable substitution to show that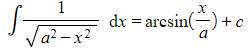
Let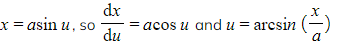
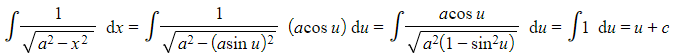
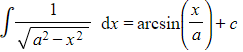
The general idea in these types of problems is to reduce the denominator to a single term, often involving the identity , so it can be integrated using standard results or techniques
- Type 2
Reverse chain rule, possibly involving some factorising in the denominator and using ‘adjust’ and ‘compensate’ if necessary
e.g. Find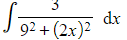
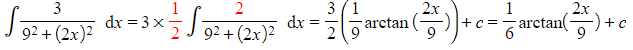
- Type 3
The denominator contains a three-term quadratic expression – i.e. there is an x term
In such cases complete the square and use reverse chain rule
e.g. Find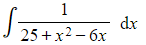
![]()
- (This works since
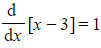 , so effectively there is no reverse chain rule involved)
, so effectively there is no reverse chain rule involved)
- A fourth type of problem may involve a given substitution but the skills to solve these are covered in the A Level Mathematics course
How do I use a trigonometric substitution to find integrals?
- STEP 1
Identify the type of problem and if a substitution is required
Determine the substitution if needed - STEP 2
For Type 1 problems, differentiate and rearrange the substitution; change everything in the integral
For Type 2 problems, ‘adjust’ and ‘compensate’ as necessary
For Type 3 problems complete the square - STEP 3
Integrate using standard techniques and results, possibly from the formulae booklet
For definite integration, a calculator may be used but look out for exact values being required, a calculator may give an approximation - STEP 4
Substitute the original variable back in if necessary – this shouldn’t be necessary for definite integration
For indefinite integration, simplify where obvious and/or rearrange into a required format
Why is arccos x not involved in any of the integration results?
For integration the "-" at the start can be treated as the constant "-1" and so integrating would lead to "-arcsin ..."
-
- i.e.
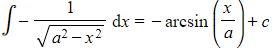
- i.e.
Exam Tip
- The general form of the functions involving trigonometric and hyperbolic functions are very similar
- Be clear about which form needs a trigonometric substitution and which form need a hyperbolic substitution
- Always have a copy of the formula booklet to hand when practising these problems
Worked Example
(a) Use an appropriate substitution to show that
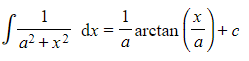

(b) Find
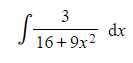

Integrating using Hyperbolic Substitutions
The integrals covered in this revision note are based on the standard results
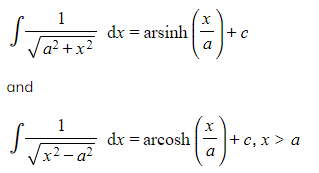
These are given in the formulae booklet
How do I know when to use a hyperbolic substitution in integration?
There are three main types of problem

- A fourth type of problem may involve a given substitution but the skills to solve these are covered in the A Level Mathematics course, although hyperbolic functions are not
How do I use a hyperbolic substitution to find integrals?
- STEP 1
Identify the type of problem and if a substitution is required
Determine the substitution if needed - STEP 2
For Type 1 problems, differentiate and rearrange the substitution; change everything in the integral
For Type 2 problems, ‘adjust’ and ‘compensate’ as necessary
For Type 3 problems complete the square - STEP 3
Integrate using standard techniques and results, possibly from the formulae booklet
For definite integration, a calculator may be used but look out for exact values being required, a calculator may give an approximation - STEP 4
Substitute the original variable back in if necessary – this shouldn’t be necessary for definite integration
For indefinite integration, simplify where obvious and/or rearrange into a required format
Is artanh x involved in integration?
- The standard result, given in the formulae booklet is
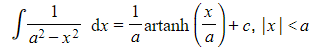
with the alternative result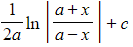 also given
also given - Problems involving these often involve partial fractions (since
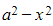 is the difference of two squares) leading to the 'ln' result
is the difference of two squares) leading to the 'ln' result - If you happen to recognise the integral and can use the formulae booklet result involving "artanh" to solve a problem, then do so!
Exam Tip
- The general form of the functions involving trigonometric and hyperbolic functions are very similar
- Be clear about which form needs a trigonometric substitution and which form need a hyperbolic substitution
- Always have a copy of the formula booklet to hand when practising these problems
Worked Example
(a) Use an appropriate substitution to show that
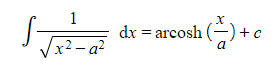

(b) Find
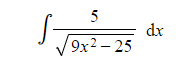

转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1