- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2011 AIME I真题及答案解析
2011 AIME I真题
答案解析请参考文末
Problem 1
Jar A contains four liters of a solution that is ![]() acid. Jar B contains five liters of a solution that is
acid. Jar B contains five liters of a solution that is ![]() acid. Jar C contains one liter of a solution that is
acid. Jar C contains one liter of a solution that is ![]() acid. From jar C,
acid. From jar C,![]() liters of the solution is added to jar A, and the remainder of the solution in jar C is added to jar B. At the end both jar A and jar B contain solutions that are
liters of the solution is added to jar A, and the remainder of the solution in jar C is added to jar B. At the end both jar A and jar B contain solutions that are ![]() acid. Given that
acid. Given that ![]() and
and ![]() are relatively prime positive integers, find
are relatively prime positive integers, find ![]() .
.
Problem 2
In rectangle ![]() ,
, ![]() and
and ![]() . Points
. Points ![]() and
and ![]() lie inside rectangle
lie inside rectangle ![]() so that
so that ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and line
, and line ![]() intersects segment
intersects segment ![]() . The length
. The length ![]() can be expressed in the form
can be expressed in the form ![]() , where
, where ![]() ,
, ![]() , and
, and ![]() are positive integers and
are positive integers and ![]() is not divisible by the square of any prime. Find
is not divisible by the square of any prime. Find ![]() .
.
Problem 3
Let ![]() be the line with slope
be the line with slope ![]() that contains the point
that contains the point ![]() , and let
, and let ![]() be the line perpendicular to line
be the line perpendicular to line ![]() that contains the point
that contains the point ![]() . The original coordinate axes are erased, and line
. The original coordinate axes are erased, and line ![]() is made the
is made the ![]() -axis and line
-axis and line ![]() the
the ![]() -axis. In the new coordinate system, point
-axis. In the new coordinate system, point ![]() is on the positive
is on the positive ![]() -axis, and point
-axis, and point ![]() is on the positive
is on the positive ![]() -axis. The point
-axis. The point ![]() with coordinates
with coordinates ![]() in the original system has coordinates
in the original system has coordinates ![]() in the new coordinate system. Find
in the new coordinate system. Find ![]() .
.
Problem 4
In triangle ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . The angle bisector of angle
. The angle bisector of angle ![]() intersects
intersects ![]() at point
at point ![]() , and the angle bisector of angle
, and the angle bisector of angle ![]() intersects
intersects ![]() at point
at point ![]() . Let
. Let ![]() and
and ![]() be the feet of the perpendiculars from
be the feet of the perpendiculars from ![]() to
to ![]() and
and ![]() , respectively. Find
, respectively. Find ![]() .
.
Problem 5
The vertices of a regular nonagon (9-sided polygon) are to be labeled with the digits 1 through 9 in such a way that the sum of the numbers on every three consecutive vertices is a multiple of 3. Two acceptable arrangements are considered to be indistinguishable if one can be obtained from the other by rotating the nonagon in the plane. Find the number of distinguishable acceptable arrangements.
Problem 6
Suppose that a parabola has vertex ![]() and equation
and equation ![]() , where
, where ![]() and
and ![]() is an integer. The minimum possible value of
is an integer. The minimum possible value of ![]() can be written in the form
can be written in the form ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Problem 7
Find the number of positive integers ![]() for which there exist nonnegative integers
for which there exist nonnegative integers ![]() ,
, ![]() ,
, ![]() ,
,![]() such that
such that![\[m^{x_0} = \sum_{k = 1}^{2011} m^{x_k}.\]](http://latex.artofproblemsolving.com/3/7/c/37c3a4d8143a7bc88f260f55b43ac3f3fbb7678e.png)
Problem 8
In triangle ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Points
. Points ![]() and
and ![]() are on
are on ![]() with
with ![]() on
on![]() , points
, points ![]() and
and ![]() are on
are on ![]() with
with ![]() on
on ![]() , and points
, and points ![]() and
and ![]() are on
are on ![]() with
with ![]() on
on ![]() . In addition, the points are positioned so that
. In addition, the points are positioned so that ![]() ,
, ![]() , and
, and ![]() . Right angle folds are then made along
. Right angle folds are then made along ![]() ,
, ![]() , and
, and ![]() . The resulting figure is placed on a level floor to make a table with triangular legs. Let
. The resulting figure is placed on a level floor to make a table with triangular legs. Let ![]() be the maximum possible height of a table constructed from triangle
be the maximum possible height of a table constructed from triangle ![]() whose top is parallel to the floor. Then
whose top is parallel to the floor. Then ![]() can be written in the form
can be written in the form ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers and
are relatively prime positive integers and ![]() is a positive integer that is not divisible by the square of any prime. Find
is a positive integer that is not divisible by the square of any prime. Find ![]() .
.
![[asy] unitsize(1 cm); pair translate; pair[] A, B, C, U, V, W, X, Y, Z; A[0] = (1.5,2.8); B[0] = (3.2,0); C[0] = (0,0); U[0] = (0.69*A[0] + 0.31*B[0]); V[0] = (0.69*A[0] + 0.31*C[0]); W[0] = (0.69*C[0] + 0.31*A[0]); X[0] = (0.69*C[0] + 0.31*B[0]); Y[0] = (0.69*B[0] + 0.31*C[0]); Z[0] = (0.69*B[0] + 0.31*A[0]); translate = (7,0); A[1] = (1.3,1.1) + translate; B[1] = (2.4,-0.7) + translate; C[1] = (0.6,-0.7) + translate; U[1] = U[0] + translate; V[1] = V[0] + translate; W[1] = W[0] + translate; X[1] = X[0] + translate; Y[1] = Y[0] + translate; Z[1] = Z[0] + translate; draw (A[0]--B[0]--C[0]--cycle); draw (U[0]--V[0],dashed); draw (W[0]--X[0],dashed); draw (Y[0]--Z[0],dashed); draw (U[1]--V[1]--W[1]--X[1]--Y[1]--Z[1]--cycle); draw (U[1]--A[1]--V[1],dashed); draw (W[1]--C[1]--X[1]); draw (Y[1]--B[1]--Z[1]); dot("$A$",A[0],N); dot("$B$",B[0],SE); dot("$C$",C[0],SW); dot("$U$",U[0],NE); dot("$V$",V[0],NW); dot("$W$",W[0],NW); dot("$X$",X[0],S); dot("$Y$",Y[0],S); dot("$Z$",Z[0],NE); dot(A[1]); dot(B[1]); dot(C[1]); dot("$U$",U[1],NE); dot("$V$",V[1],NW); dot("$W$",W[1],NW); dot("$X$",X[1],dir(-70)); dot("$Y$",Y[1],dir(250)); dot("$Z$",Z[1],NE); [/asy]](http://latex.artofproblemsolving.com/a/3/3/a3378981be03ff826f3c61884709fecbe15b1ee5.png)
Problem 9
Suppose ![]() is in the interval
is in the interval ![]() and
and ![]() . Find
. Find ![]() .
.
Problem 10
The probability that a set of three distinct vertices chosen at random from among the vertices of a regular ![]() -gon determine an obtuse triangle is
-gon determine an obtuse triangle is ![]() . Find the sum of all possible values of
. Find the sum of all possible values of ![]() .
.
Problem 11
Let ![]() be the set of all possible remainders when a number of the form
be the set of all possible remainders when a number of the form ![]() ,
, ![]() a nonnegative integer, is divided by 1000. Let
a nonnegative integer, is divided by 1000. Let ![]() be the sum of the elements in
be the sum of the elements in ![]() . Find the remainder when
. Find the remainder when ![]() is divided by 1000.
is divided by 1000.
Problem 12
Six men and some number of women stand in a line in random order. Let ![]() be the probability that a group of at least four men stand together in the line, given that every man stands next to at least one other man. Find the least number of women in the line such that
be the probability that a group of at least four men stand together in the line, given that every man stands next to at least one other man. Find the least number of women in the line such that ![]() does not exceed 1 percent.
does not exceed 1 percent.
Problem 13
A cube with side length 10 is suspended above a plane. The vertex closest to the plane is labeled![]() . The three vertices adjacent to vertex
. The three vertices adjacent to vertex ![]() are at heights 10, 11, and 12 above the plane. The distance from vertex
are at heights 10, 11, and 12 above the plane. The distance from vertex ![]() to the plane can be expressed as
to the plane can be expressed as ![]() , where
, where ![]() ,
, ![]() , and
, and ![]() are positive integers. Find
are positive integers. Find ![]() .
.
Problem 14
Let ![]() be a regular octagon. Let
be a regular octagon. Let ![]() ,
, ![]() ,
, ![]() , and
, and ![]() be the midpoints of sides
be the midpoints of sides ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , respectively. For
, respectively. For ![]() , ray
, ray ![]() is constructed from
is constructed from ![]() towards the interior of the octagon such that
towards the interior of the octagon such that ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Pairs of rays
. Pairs of rays ![]() and
and ![]() ,
, ![]() and
and ![]() ,
, ![]() and
and ![]() , and
, and ![]() and
and ![]() meet at
meet at ![]() ,
, ![]() ,
, ![]() ,
, ![]() respectively. If
respectively. If ![]() , then
, then ![]() can be written in the form
can be written in the form ![]() , where
, where ![]() and
and ![]() are positive integers. Find
are positive integers. Find ![]() .
.
Problem 15
For some integer ![]() , the polynomial
, the polynomial ![]() has the three integer roots
has the three integer roots ![]() ,
, ![]() , and
, and ![]() . Find
. Find ![]() .
.
2011 AIME I答案及解析请注册或登录后查看:
以上解析方式仅供参考
AMC8/AMC10/AMC12/AIME
相关咨询及辅导
欢迎扫码联系下方翰林学术活动顾问李老师


Aaron 李老师 15618605663 微信:linstitute4
翰林AIME课程体系流程图
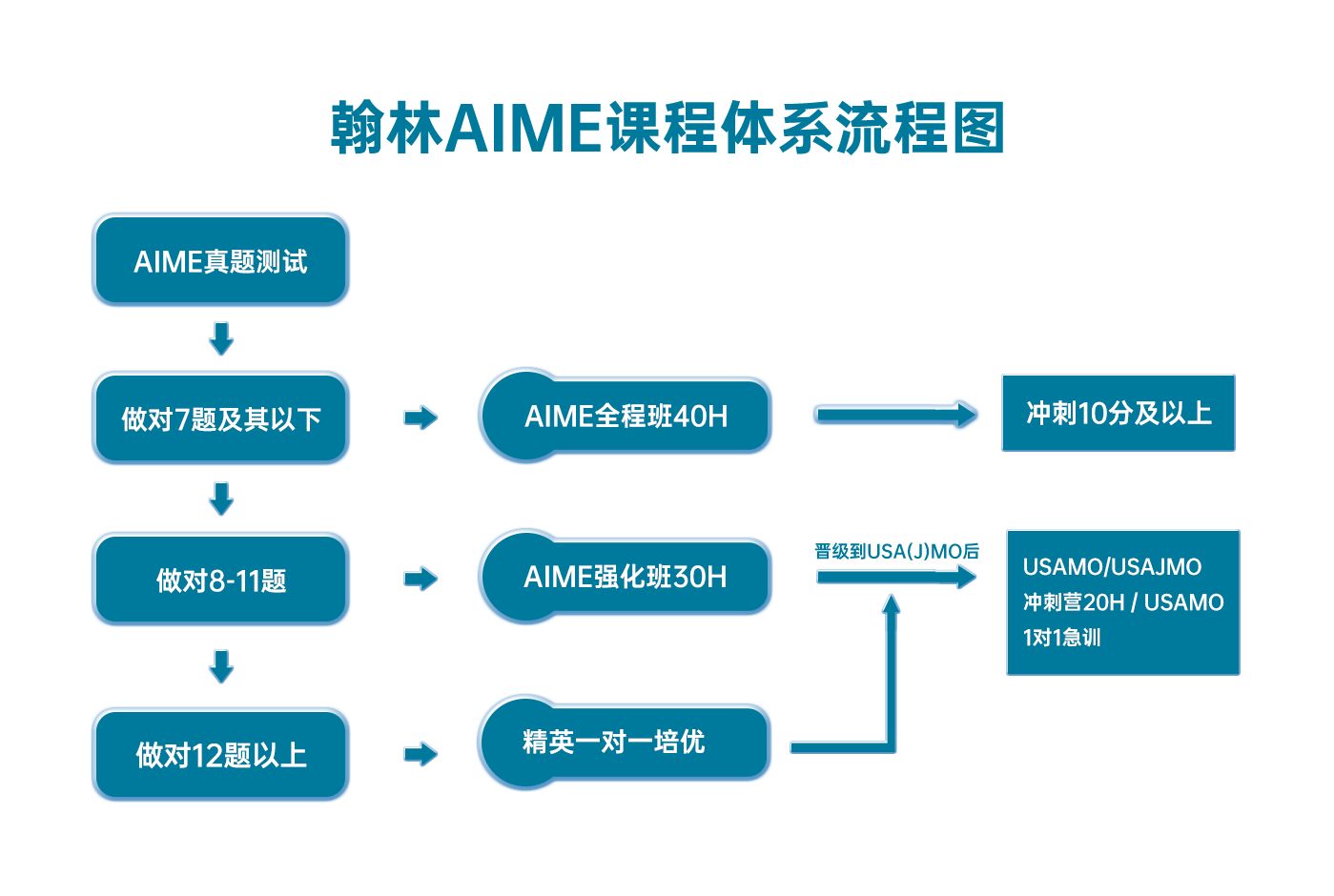
-

二年级低龄数学竞赛备赛班
¥14,900.00 Add to cart -

3-4年级低龄数学竞赛备赛班
¥14,900.00 Add to cart -

北美驯鹿数学竞赛一对一
¥999.00 Add to cart -

紫色彗星数学竞赛一对一
¥999.00 Add to cart -

2024AMC8强化班
¥21,900.00 Add to cart -

2023AMC8大班课程
¥21,900.00 Add to cart -

2023 AMC10一对一
¥1,199.00 Add to cart -

2023AMC10强化班-40课时
¥23,900.00 Add to cart -

2023 AMC10数学竞赛基础班
¥23,900.00 Add to cart -

2023 AMC10数学竞赛全程班
¥32,900.00 Add to cart
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1







