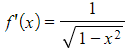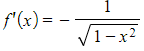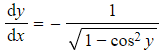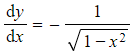- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Further Maths: Core Pure:复习笔记5.2.4 Calculus involving Inverse Trig
Differentiating Inverse Trig Functions
What are the inverse trigonometric functions?
- arcsin, arccos and arctan are functions defined as the inverse functions of sine, cosine and tangent respectively
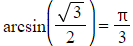 which is equivalent to
which is equivalent to 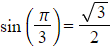
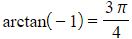 which is equivalent to
which is equivalent to 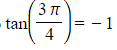
What are the derivatives of the inverse trigonometric functions?
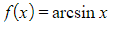
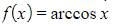
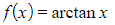
- Unlike other derivatives these look completely unrelated at first
- their derivation involves use of the identity
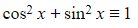
- hence the squares and square roots!
- their derivation involves use of the identity
- All three are given in the formula booklet
- Note with the derivative of
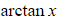 that
that 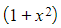 is the same as
is the same as 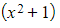
How do I show or prove the derivatives of the inverse trigonometric functions?
- For
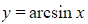
- Rewrite,

- Differentiate implicitly,
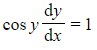
- Rearrange,

- Using the identity
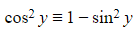 rewrite,
rewrite, 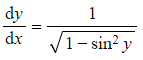
- Since,
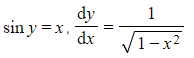
- Rewrite,
- Similarly, for
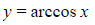
- Notice how the derivative of
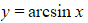 is positive but is negative for
is positive but is negative for 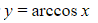
- This subtle but crucial difference can be seen in their graphs
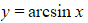 has a positive gradient for all values of
has a positive gradient for all values of 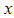 in its domain
in its domain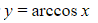 has a negative gradient for all values of
has a negative gradient for all values of 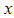 in its domain
in its domain
- This subtle but crucial difference can be seen in their graphs
Exam Tip
- For
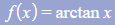 the terms on the denominator can be reversed (as they are being added rather than subtracted)
the terms on the denominator can be reversed (as they are being added rather than subtracted)
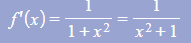
- Don't be fooled by this, it sounds obvious but on awkward "show that" questions it can be off-putting!
Worked Example
a) Show that the derivative of ![]() is
is 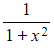

b) Find the derivative of 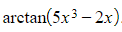 .
.

Integrating Inverse Trig Functions
How do I integrate inverse trig functions?
- Use integration by parts in the same way you would integrate
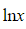
- These can be integrated using parts however
- rewrite as the product ‘
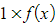 ’ and choose
’ and choose 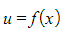 and
and 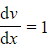
- 1 is easy to integrate and the inverse trig functions have standard derivatives listed in the formula booklet
- rewrite as the product ‘
- The expression
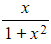 integrates to
integrates to 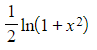
- The expression
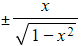 integrates to
integrates to 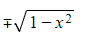
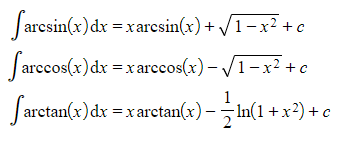
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1