- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Further Maths: Core Pure:复习笔记5.1.1 Volumes of Revolution
Volumes of revolution around the x-axis
What is a volume of revolution around the x-axis?
- A solid of revolution is formed when an area bounded by a function
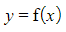 (and other boundary equations) is rotated 360° around the x-axis
(and other boundary equations) is rotated 360° around the x-axis - A volume of revolution is the volume of this solid formed
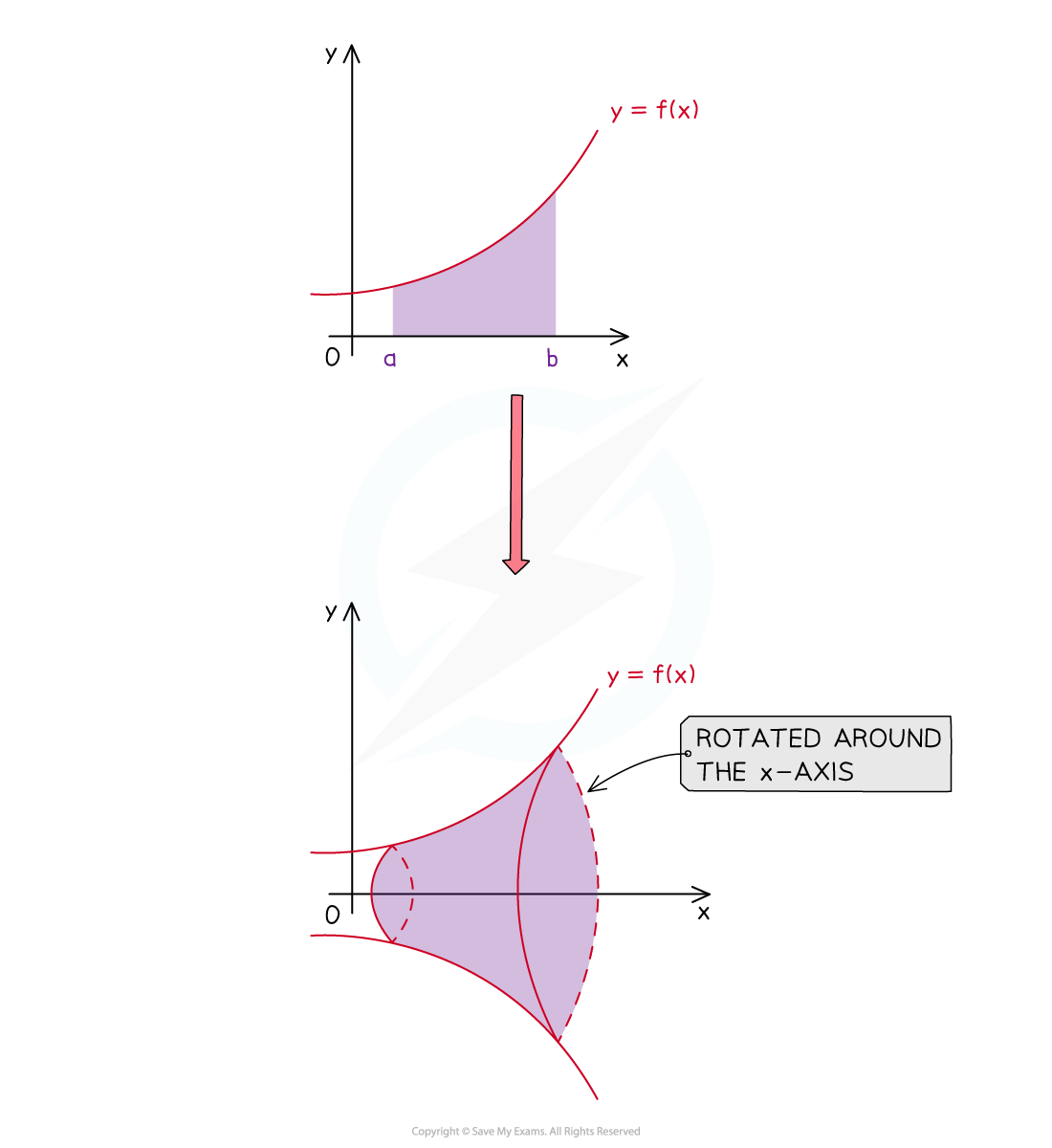
Example of a solid of revolution that is formed by rotating the area bounded by the function ![]() , the lines
, the lines ![]() and
and ![]() and the
and the ![]() -axis
-axis ![]() about the
about the ![]() -axis
-axis
How do I find the volume of revolution around the x-axis?
- To find the volume of revolution created when the area bounded by the function
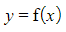 , the lines
, the lines 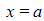 and
and 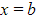 , and the x-axis is rotated 360° about the x-axis use the formula
, and the x-axis is rotated 360° about the x-axis use the formula
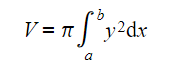
- The formula may look complicated or confusing at first due to the y and dx
- remember that y is a function of x
- once the expression for y is substituted in, everything will be in terms of x
- π is a constant so you may see this written either inside or outside the integral
- This is not given in the formulae booklet
- The formulae booklet does list the volume formulae for some common 3D solids – it may be possible to use these depending on what information about the solid is available
Where does the formula for the volume of revolution come from?
- When you integrate to find the area under a curve you can see the formula by splitting the area into rectangles with small widths
- The same method works for volumes
- Split the volume into cylinders with small widths
- The radius will be the y value
- The width will be a small interval along the x-axis δx
- The volume can be approximated by the sum of the volumes of these cylinders
![]()
- The limit as δx goes to zero can be found by integration - just like with areas
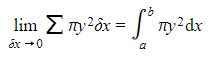
How do I solve problems involving volumes of revolution around the x-axis?
- Visualising the solid created is helpful
- Try sketching some functions and their solids of revolution to help
- STEP 1 Square y
- Do this first without worrying about π or the integration and limits
- STEP 2 Identify the limits a and b (which could come from a graph)
- STEP 3 Use the formula by evaluating the integral and multiplying by π
- The answer may be required in exact form (leave in terms of π)
- If not, round to three significant figures (unless told otherwise)
- The answer may be required in exact form (leave in terms of π)
- Trickier questions may give you the volume and ask for the value of an unknown constant elsewhere in the problem
Exam Tip
- To help remember the formula note that it is only
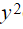 - volume is 3D so you may have expected a cubic expression
- volume is 3D so you may have expected a cubic expression
- If rotating a single point around the x-axis a circle of radius would be formed
- The area of that circle would then be
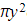
- Integration then adds up the areas of all circles between a and b creating the third dimension and volume
(In 2D, integration creates area by adding up lots of 1D lines)
- The area of that circle would then be
- If rotating a single point around the x-axis a circle of radius would be formed
Worked Example
Find the volume of the solid of revolution formed by rotating the region bounded by the graph of ![]() , the coordinate axes and the line
, the coordinate axes and the line ![]() radians around the χ-axis. Give your answer as an exact multiple of
radians around the χ-axis. Give your answer as an exact multiple of ![]() .
.
Volumes of revolution around the y-axis
What is a volume of revolution around the y-axis?
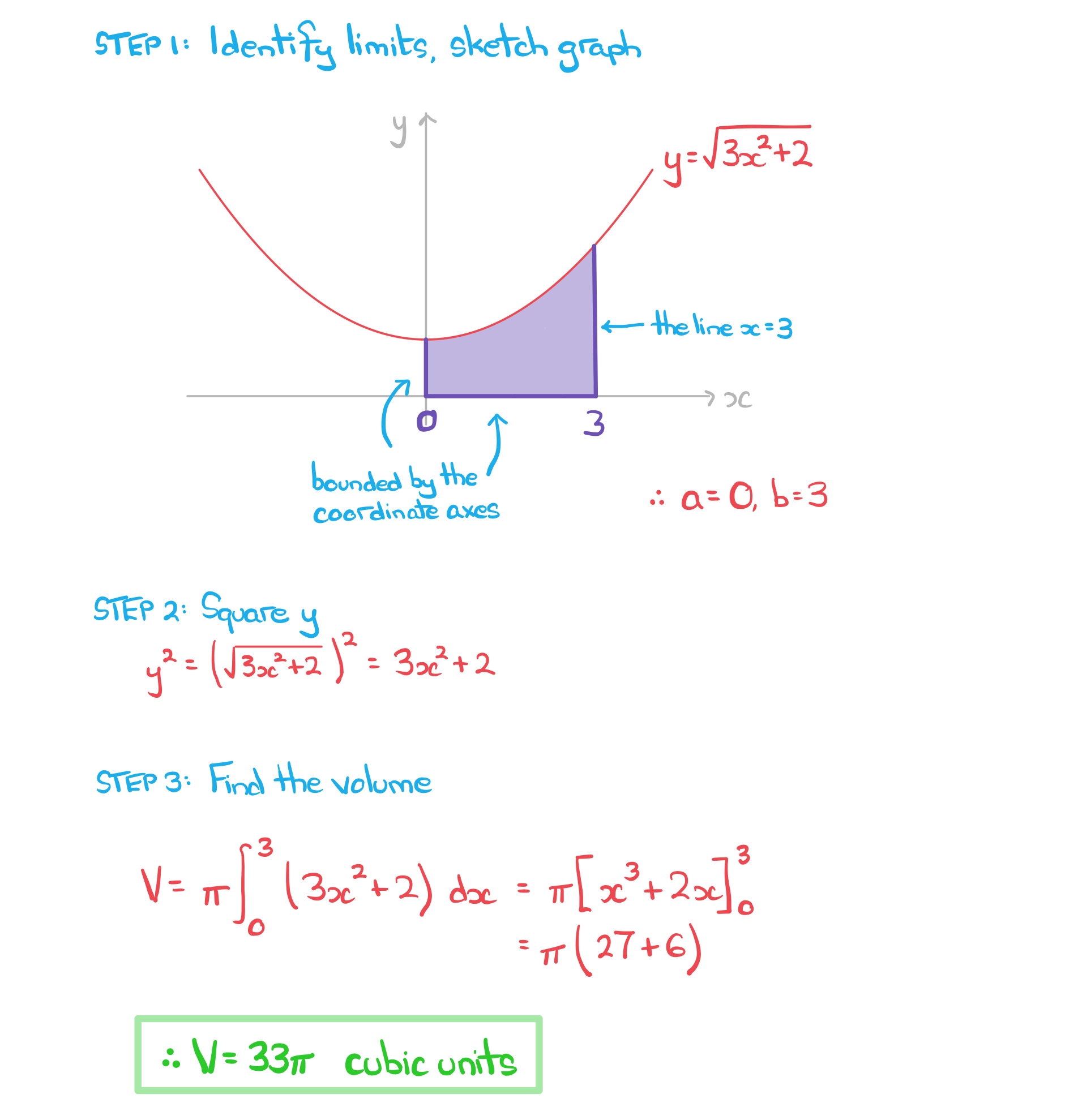
- A solid of revolution is formed when an area bounded by a function
 (and other boundary equations) is rotated 360° around the y-axis
(and other boundary equations) is rotated 360° around the y-axis - A volume of revolution is the volume of this solid formed
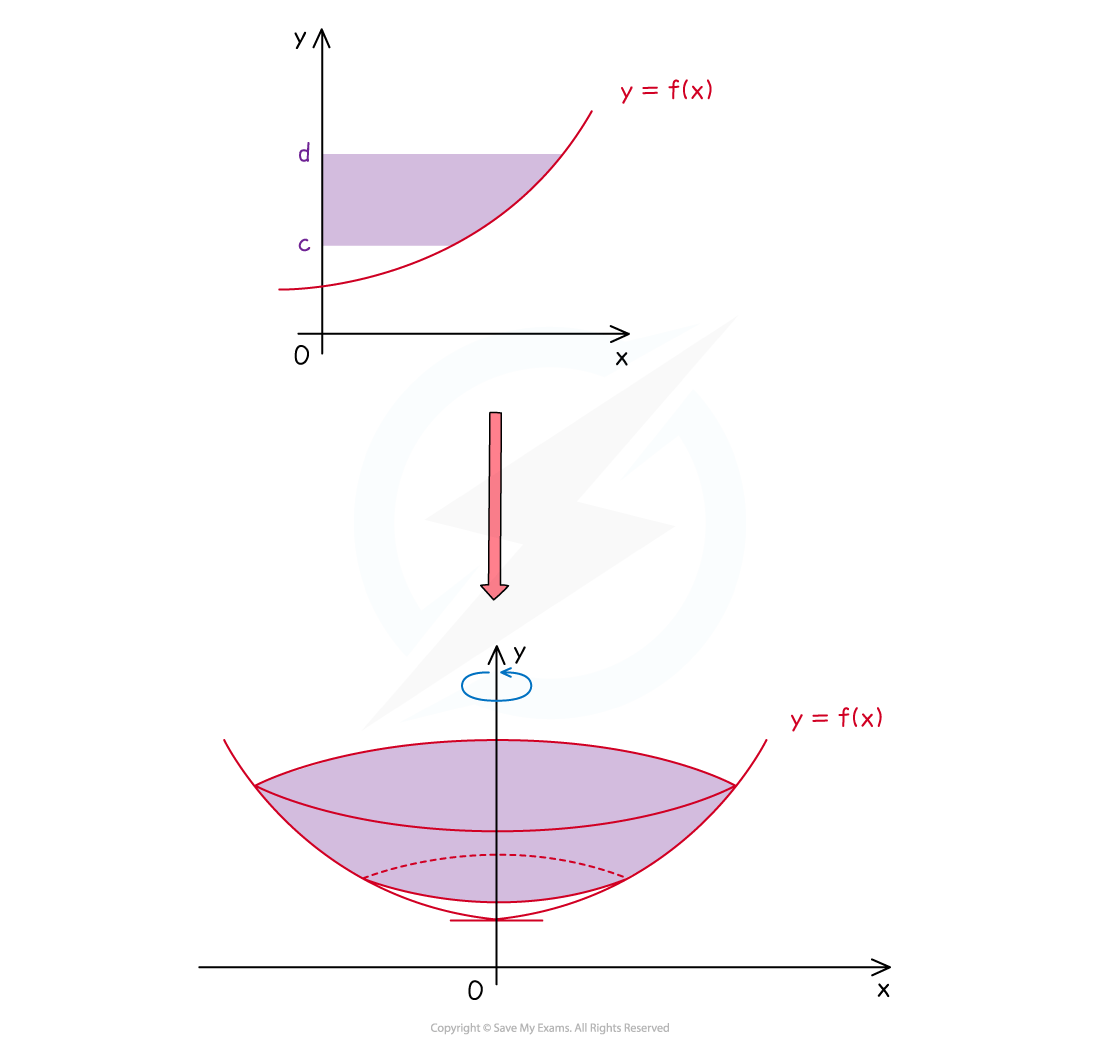
Example of a solid of revolution that is formed by rotating the area bounded by the function![]() , the lines
, the lines ![]() and
and ![]() and the
and the ![]() -axis
-axis ![]() about the
about the ![]() -axis
-axis
How do I find the volume of revolution around the y-axis?
- To find the volume of revolution created when the area bounded by the function
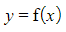 , the lines
, the lines 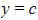 and
and 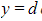 , and the y-axis is rotated 360° about the y-axis use the formula
, and the y-axis is rotated 360° about the y-axis use the formula
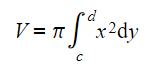
- Note that although the function may be given in the form
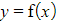 it will first need rewriting in the form
it will first need rewriting in the form 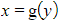
- This is not given in the formulae booklet
How do I solve problems involving volumes of revolution around the y-axis?
- Visualising the solid created is helpful
- Try sketching some functions and their solids of revolution to help
- STEP 1 Rearrange
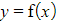 into the form
into the form 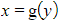 (if necessary)
(if necessary)
- This is finding the inverse function
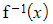
- This is finding the inverse function
- STEP 2 Square x
- Do this first without worrying about π or the integration and limits
- STEP 3 Identify the limits c and d (which could come from a graph)
- STEP 4 Use the formula by evaluating the integral and multiplying by π
- The answer may be required in exact form (leave in terms of π)
- If not, round to three significant figures (unless told otherwise)
- The answer may be required in exact form (leave in terms of π)
- Trickier questions may give you the volume and ask for the value of an unknown constant elsewhere in the problem
Exam Tip
- Double check questions to ensure you are clear about which axis the rotation is around
- Separating the rearranging of
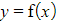 into
into 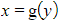 and the squaring of x is important for maintaining accuracy
and the squaring of x is important for maintaining accuracy
- In some cases it can seem as though x has been squared twice
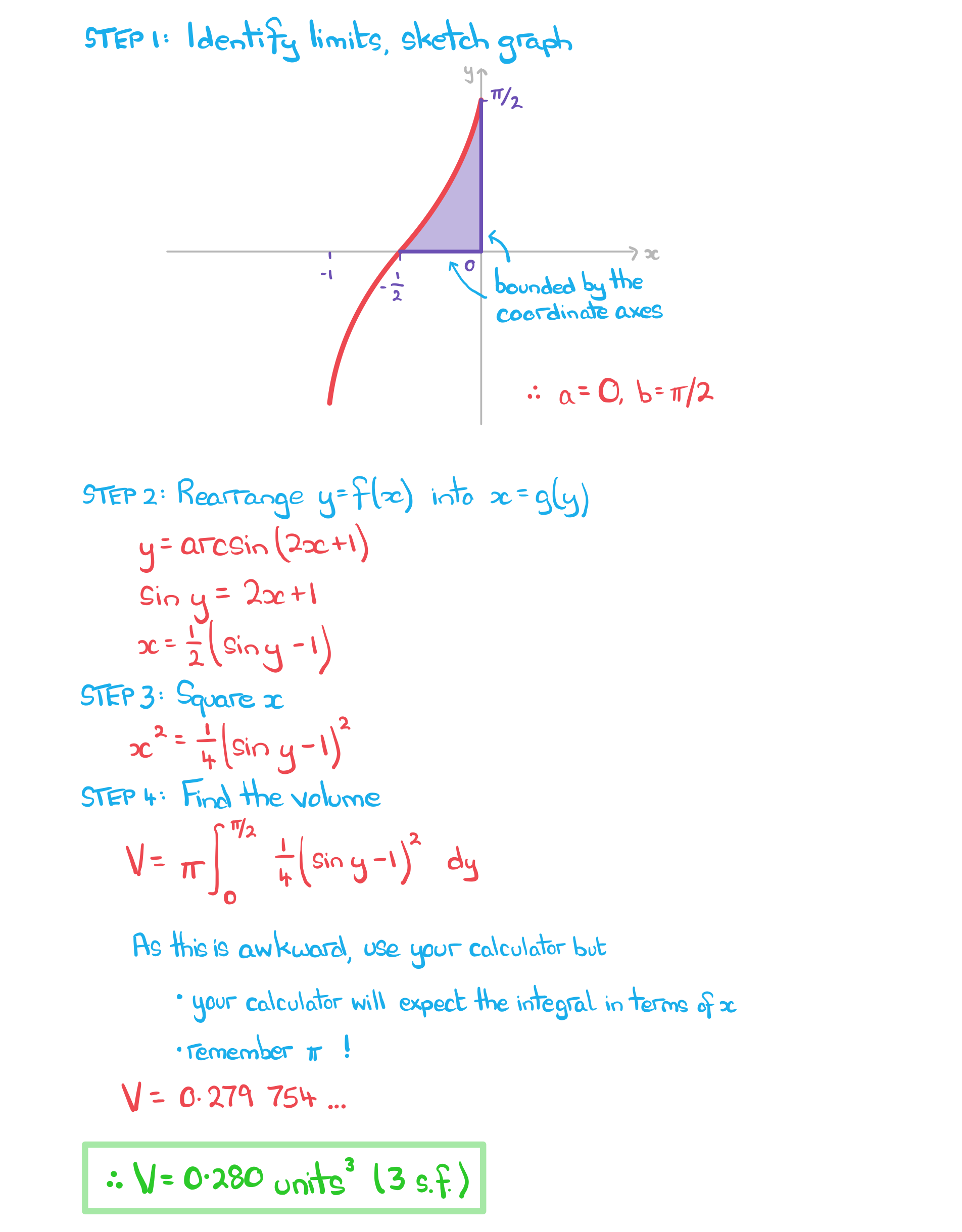
Worked Example
Find the volume of the solid of revolution formed by rotating the region bounded by the graph of ![]() and the coordinate axes by
and the coordinate axes by ![]() radians around the
radians around the ![]() -axis. Give your answer to three significant figures.
-axis. Give your answer to three significant figures.
Volumes of Revolution using Parametric Equations
What is parametric volumes of revolution?
- Solids of revolution are formed by rotating functions about the x-axis or the y-axis
- Here though, rather than given y in terms of x, both x and y are given in terms of a parameter, t
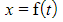
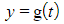
- Depending on the nature of the functions f and g it may not be convenient or possible to find y in terms of x
How do I find volumes of revolution when x and y are given parametrically?
- The aim is to replace everything in the ‘original’ integral so that it is in terms of t
- For the ‘original’ integral
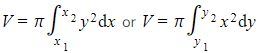 and parametric equations given in the form
and parametric equations given in the form  use the following process
use the following process - STEP 1: Find dx or dy in terms of t and dt
- STEP 2: If necessary, change the limits from x values or y values to t values using
-
- STEP 3: Square y or x
-
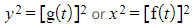
- Do this separately to avoid confusing when putting the integral together
-
- STEP 4: Set up the integral, so everything is now in terms of t, simplify where possible and evaluate the integral to find the volume of revolution
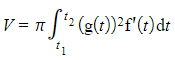 (if around x-axis) or
(if around x-axis) or 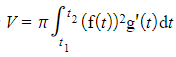 (if around y-axis)
(if around y-axis)
Exam Tip
- Avoid the temptation to jump straight to STEP 4
- There could be a lot to change and simplify in exam style problems
- Doing each step carefully helps maintain high levels of accuracy
Worked Example
The curve C is defined parametrically by ![]() and
and ![]() . C is rotated 360° about the x-axis between the values of
. C is rotated 360° about the x-axis between the values of ![]() and
and ![]() . Show that the volume of the solid of revolution generated by this rotation is
. Show that the volume of the solid of revolution generated by this rotation is ![]() cubic units where
cubic units where ![]() and
and ![]() are integers to be found.
are integers to be found.

转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





