- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Further Maths: Core Pure:复习笔记3.2.2 Method of Differences
Method of Differences
What is the Method of Differences?
- The Method of Differences is a way of turning longer and more complicated sums into shorter and simpler ones
- Sometimes when summing series, you will notice that many of the terms (or parts of the terms) simply “cancel out” or eliminate each other
- This can turn a very long series summation, into a much simpler shorter one
- In the case of
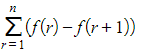
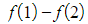
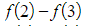
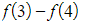
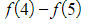
- (and so on, until…)
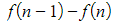
- This is the penultimate term
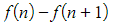
- This is the last term
- You can see that when these are summed, most of the terms will cancel out
- This leaves just
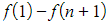
- We can say that
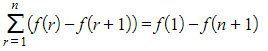
- This leaves just
How can I use partial fractions along with the method of differences?
- You will often need to use partial fractions to change the general term into a sum of two or three terms, rather than a single fraction
- For example,
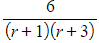 can be rewritten as
can be rewritten as 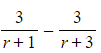
- For example,
- This may lead to a more interesting pattern of cancellations than was seen for
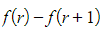
- For example,
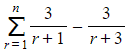 can be written as
can be written as 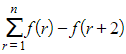 , where
, where 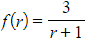 , and the terms can then be listed as:
, and the terms can then be listed as:
-
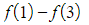
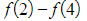
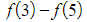
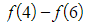
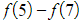
- (and so on, until…)
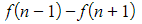
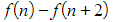
- When these are summed, it will just leave
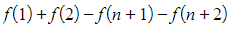
- You can then evaluate this expression with
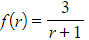 to get to your final answer
to get to your final answer
-
- It is helpful to use
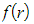 notation to spot the pattern, rather than substituting
notation to spot the pattern, rather than substituting 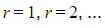 into the expression every time, especially with more complicated expressions
into the expression every time, especially with more complicated expressions
- You need to consider carefully which term to make
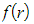 and then how the other terms in the expression relate to it
and then how the other terms in the expression relate to it - If this is difficult for a particular expression, it may be more straightforward to substitute
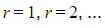 into each term in the series and spot any patterns that way
into each term in the series and spot any patterns that way - This is essentially writing the series out in full until you spot which terms will cancel
- In your working, however, you should still write out the last two or three terms in terms of
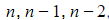 , etc.
, etc.
- You need to consider carefully which term to make
How can I use the method of differences for series with expressions containing more than two terms?
- The general term of the series may have more than two terms, which can sometimes make spotting which terms will cancel more challenging
- For example,
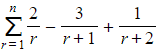
- This can be written as
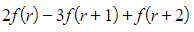 where
where 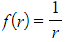
- Writing out the first five terms and the last three terms we get:
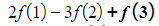
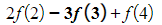
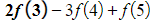
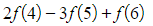
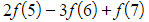
- (and so on until…)
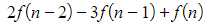
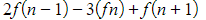
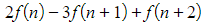
- In this case, look at the diagonals starting at the top right
- We have
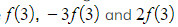 which sum to o
which sum to o - This pattern repeats for the other diagonals
- We have
- We will eventually be left with only
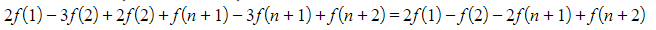
- Evaluating this with
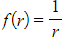 results in an answer of
results in an answer of 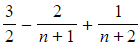
- For example,
What other uses are there for the method of differences?
- Method of differences can also be used to prove the formulae for the sum of

- For example, this can be used to prove that the result for the sum of squares is indeed
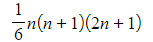
- By expanding brackets it can be shown that
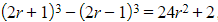 , and then the sum of both sides of that equation from
, and then the sum of both sides of that equation from  can be considered
can be considered 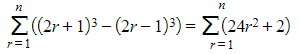
- The left-hand side can be found in terms of
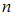 using method of differences, and the right-hand side can be rearranged to give
using method of differences, and the right-hand side can be rearranged to give 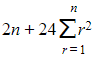
- That equation can then be rearranged to give an expression for
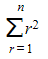
- When these proofs have appeared previously in exams, they have tended to be structured to help you work through the steps
- By expanding brackets it can be shown that
- For example, this can be used to prove that the result for the sum of squares is indeed
- You may have to use your algebraic method of differences result to find a numerical answer, usually in the last part of a question
- The question will often ask you to evaluate the sum starting from
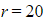 (or some other arbitrary value) rather than from
(or some other arbitrary value) rather than from 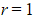
- To help with this, remember that:
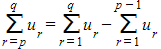
- You may also find it helpful to recall that for constants
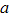 and
and 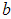 :
: 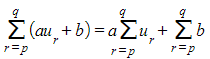
- The question will often ask you to evaluate the sum starting from
Exam Tip
- Mark schemes often specify how many terms from the start and end of the series should be written down – it is usually two or three, so always write down the first three and last three terms
- Don’t be afraid to write out more terms than this to make sure you spot the pattern, and can easily decide which terms will cancel and which will not
- Check your algebraic answer by substituting in numbers to make sure it works; you can use your calculator to find summations in sigma notation
Worked Example
(a) Express 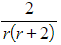 in partial fractions.
in partial fractions.

(b) Hence show that 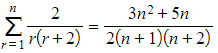 using the method of differences.
using the method of differences.
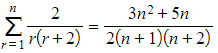 using the method of differences.
using the method of differences.

转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





