- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2010AMC10A真题与答案解析
2010AMC10A真题
答案解析请参考文末
Problem 1
Mary’s top book shelf holds five books with the following widths, in centimeters: ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . What is the average book width, in centimeters?
. What is the average book width, in centimeters?
![]()
Problem 2
Four identical squares and one rectangle are placed together to form one large square as shown. The length of the rectangle is how many times as large as its width?
![[asy] unitsize(8mm); defaultpen(linewidth(.8pt)); draw((0,0)--(4,0)--(4,4)--(0,4)--cycle); draw((0,3)--(0,4)--(1,4)--(1,3)--cycle); draw((1,3)--(1,4)--(2,4)--(2,3)--cycle); draw((2,3)--(2,4)--(3,4)--(3,3)--cycle); draw((3,3)--(3,4)--(4,4)--(4,3)--cycle); [/asy]](http://latex.artofproblemsolving.com/d/0/9/d09caec6074d6abf81a6e3a7755b2eecc103bc41.png)
![]()
Problem 3
Tyrone had ![]() marbles and Eric had
marbles and Eric had ![]() marbles. Tyrone then gave some of his marbles to Eric so that Tyrone ended with twice as many marbles as Eric. How many marbles did Tyrone give to Eric?
marbles. Tyrone then gave some of his marbles to Eric so that Tyrone ended with twice as many marbles as Eric. How many marbles did Tyrone give to Eric?
![]()
Problem 4
A book that is to be recorded onto compact discs takes ![]() minutes to read aloud. Each disc can hold up to
minutes to read aloud. Each disc can hold up to ![]() minutes of reading. Assume that the smallest possible number of discs is used and that each disc contains the same length of reading. How many minutes of reading will each disc contain?
minutes of reading. Assume that the smallest possible number of discs is used and that each disc contains the same length of reading. How many minutes of reading will each disc contain?
![]()
Problem 5
The area of a circle whose circumference is ![]() is
is ![]() . What is the value of
. What is the value of ![]() ?
?
![]()
Problem 6
For positive numbers ![]() and
and ![]() the operation
the operation ![]() is defined as
is defined as
![]()
What is ![]() ?
?
![]()
Problem 7
Crystal has a running course marked out for her daily run. She starts this run by heading due north for one mile. She then runs northeast for one mile, then southeast for one mile. The last portion of her run takes her on a straight line back to where she started. How far, in miles, is this last portion of her run?
![]()
Problem 8
Tony works ![]() hours a day and is paid $
hours a day and is paid $![]() per hour for each full year of his age. During a six month period Tony worked
per hour for each full year of his age. During a six month period Tony worked ![]() days and earned $
days and earned $![]() . How old was Tony at the end of the six month period?
. How old was Tony at the end of the six month period?
![]()
Problem 9
A palindrome, such as ![]() , is a number that remains the same when its digits are reversed. The numbers
, is a number that remains the same when its digits are reversed. The numbers ![]() and
and ![]() are three-digit and four-digit palindromes, respectively. What is the sum of the digits of
are three-digit and four-digit palindromes, respectively. What is the sum of the digits of ![]() ?
?
![]()
Problem 10
Marvin had a birthday on Tuesday, May 27 in the leap year ![]() . In what year will his birthday next fall on a Saturday?
. In what year will his birthday next fall on a Saturday?
![]()
Problem 11
The length of the interval of solutions of the inequality ![]() is
is ![]() . What is
. What is ![]() ?
?
![]()
Problem 12
Logan is constructing a scaled model of his town. The city's water tower stands 40 meters high, and the top portion is a sphere that holds 100,000 liters of water. Logan's miniature water tower holds 0.1 liters. How tall, in meters, should Logan make his tower?
![]()
Problem 13
Angelina drove at an average rate of ![]() km/h and then stopped
km/h and then stopped ![]() minutes for gas. After the stop, she drove at an average rate of
minutes for gas. After the stop, she drove at an average rate of ![]() km/h. Altogether she drove
km/h. Altogether she drove ![]() km in a total trip time of
km in a total trip time of ![]() hours including the stop. Which equation could be used to solve for the time
hours including the stop. Which equation could be used to solve for the time ![]() in hours that she drove before her stop?
in hours that she drove before her stop?
![]()
![]()
Problem 14
Triangle ![]() has
has ![]() . Let
. Let ![]() and
and ![]() be on
be on ![]() and
and ![]() , respectively, such that
, respectively, such that ![]() . Let
. Let ![]() be the intersection of segments
be the intersection of segments ![]() and
and ![]() , and suppose that
, and suppose that ![]() is equilateral. What is
is equilateral. What is ![]() ?
?
![]()
Problem 15
In a magical swamp there are two species of talking amphibians: toads, whose statements are always true, and frogs, whose statements are always false. Four amphibians, Brian, Chris, LeRoy, and Mike live together in this swamp, and they make the following statements.
Brian: "Mike and I are different species."
Chris: "LeRoy is a frog."
LeRoy: "Chris is a frog."
Mike: "Of the four of us, at least two are toads."
How many of these amphibians are frogs?
![]()
Problem 16
Nondegenerate ![]() has integer side lengths,
has integer side lengths, ![]() is an angle bisector,
is an angle bisector, ![]() , and
, and ![]() . What is the smallest possible value of the perimeter?
. What is the smallest possible value of the perimeter?
![]()
Problem 17
A solid cube has side length ![]() inches. A
inches. A ![]() -inch by
-inch by ![]() -inch square hole is cut into the center of each face. The edges of each cut are parallel to the edges of the cube, and each hole goes all the way through the cube. What is the volume, in cubic inches, of the remaining solid?
-inch square hole is cut into the center of each face. The edges of each cut are parallel to the edges of the cube, and each hole goes all the way through the cube. What is the volume, in cubic inches, of the remaining solid?
![]()
Problem 18
Bernardo randomly picks 3 distinct numbers from the set ![]() and arranges them in descending order to form a 3-digit number. Silvia randomly picks 3 distinct numbers from the set
and arranges them in descending order to form a 3-digit number. Silvia randomly picks 3 distinct numbers from the set ![]() and also arranges them in descending order to form a 3-digit number. What is the probability that Bernardo's number is larger than Silvia's number?
and also arranges them in descending order to form a 3-digit number. What is the probability that Bernardo's number is larger than Silvia's number?
![]()
Problem 19
Equiangular hexagon ![]() has side lengths
has side lengths ![]() and
and ![]() . The area of
. The area of ![]() is
is ![]() of the area of the hexagon. What is the sum of all possible values of
of the area of the hexagon. What is the sum of all possible values of ![]() ?
?
![]()
Problem 20
A fly trapped inside a cubical box with side length ![]() meter decides to relieve its boredom by visiting each corner of the box. It will begin and end in the same corner and visit each of the other corners exactly once. To get from a corner to any other corner, it will either fly or crawl in a straight line. What is the maximum possible length, in meters, of its path?
meter decides to relieve its boredom by visiting each corner of the box. It will begin and end in the same corner and visit each of the other corners exactly once. To get from a corner to any other corner, it will either fly or crawl in a straight line. What is the maximum possible length, in meters, of its path?
![]()
![]()
Problem 21
The polynomial ![]() has three positive integer roots. What is the smallest possible value of
has three positive integer roots. What is the smallest possible value of ![]() ?
?
![]()
Problem 22
Eight points are chosen on a circle, and chords are drawn connecting every pair of points. No three chords intersect in a single point inside the circle. How many triangles with all three vertices in the interior of the circle are created?
![]()
Problem 23
Each of 2010 boxes in a line contains a single red marble, and for ![]() , the box in the
, the box in the![]() position also contains
position also contains ![]() white marbles. Isabella begins at the first box and successively draws a single marble at random from each box, in order. She stops when she first draws a red marble. Let
white marbles. Isabella begins at the first box and successively draws a single marble at random from each box, in order. She stops when she first draws a red marble. Let ![]() be the probability that Isabella stops after drawing exactly
be the probability that Isabella stops after drawing exactly ![]() marbles. What is the smallest value of
marbles. What is the smallest value of ![]() for which
for which ![]() ?
?
![]()
Problem 24
The number obtained from the last two nonzero digits of ![]() is equal to
is equal to ![]() . What is
. What is ![]() ?
?
![]()
Problem 25
Jim starts with a positive integer ![]() and creates a sequence of numbers. Each successive number is obtained by subtracting the largest possible integer square less than or equal to the current number until zero is reached. For example, if Jim starts with
and creates a sequence of numbers. Each successive number is obtained by subtracting the largest possible integer square less than or equal to the current number until zero is reached. For example, if Jim starts with ![]() , then his sequence contains
, then his sequence contains![]() numbers:
numbers:
![[begin{array}{ccccc} {}&{}&{}&{}&55 55&-&7^2&=&6 6&-&2^2&=&2 2&-&1^2&=&1 1&-&1^2&=&0 end{array}]](http://latex.artofproblemsolving.com/2/e/d/2eda46643f3b6313f65bb202d501f3391552655b.png)
Let ![]() be the smallest number for which Jim’s sequence has
be the smallest number for which Jim’s sequence has ![]() numbers. What is the units digit of
numbers. What is the units digit of ![]() ?
?
![]()
2010AMC10A详细解析
- To find the average, we add up the widths
 ,
,  ,
,  ,
,  , and
, and  , to get a total sum of
, to get a total sum of  . Since there are
. Since there are  books, the average book width is
books, the average book width is  The answer is
The answer is  .
. - Let the length of the small square be
 , intuitively, the length of the big square is
, intuitively, the length of the big square is  . It can be seen that the width of the rectangle is
. It can be seen that the width of the rectangle is  . Thus, the length of the rectangle is
. Thus, the length of the rectangle is  times large as the width. The answer is
times large as the width. The answer is  .
. - Let
 be the number of marbles Tyrone gave to Eric. Then,
be the number of marbles Tyrone gave to Eric. Then,  . Solving for
. Solving for  yields
yields  and
and  . The answer is
. The answer is  .
. - Assuming that there were fractions of compact discs, it would take
 CDs to have equal reading time. However, since the number of discs can only be a whole number, there are at least 8 CDs, in which case it would have
CDs to have equal reading time. However, since the number of discs can only be a whole number, there are at least 8 CDs, in which case it would have  minutes on each of the 8 discs. The answer is
minutes on each of the 8 discs. The answer is  .
. - If the circumference of a circle is
 , the radius would be
, the radius would be  . Since the area of a circle is
. Since the area of a circle is  , the area is
, the area is  . The answer is
. The answer is  .
.  . Then,
. Then,  is
is  The answer is
The answer is 
- Crystal first runs North for one mile. Changing directions, she runs Northeast for another mile. The angle difference between North and Northeast is 45 degrees. She then switches directions to Southeast, meaning a 90 degree angle change. The distance now from traveling North for one mile, and her current destination is
 miles, because it is the hypotenuse of a 45-45-90 triangle with side length one (mile). Therefore, Crystal's distance from her starting position, x, is equal to
miles, because it is the hypotenuse of a 45-45-90 triangle with side length one (mile). Therefore, Crystal's distance from her starting position, x, is equal to  , which is equal to
, which is equal to  . The answer is
. The answer is 
![[asy] import olympiad; draw((0,0)--(0,1)); draw((0,1)--(0,1.7071067811865476), dotted); draw((0,1)--(0.7071067811865476, 1.7071067811865476)); draw((0.7071067811865476, 1.7071067811865476)--(1.4142135623730951,1)); draw(anglemark((0.7071067811865476, 1.7071067811865476),(0,1),(0,1.7071067811865476))); label("$45^{circ}$", (0,1.25), NE); draw((0, 1)--(1.4142135623730951,1), dotted); draw((1.4142135623730951,1)--(0,0), green); [/asy]](http://latex.artofproblemsolving.com/4/f/8/4f85e07c71fb200daeb9e875a79276f9b0c38b4a.png)
- Tony worked
 hours a day and is paid
hours a day and is paid  dollars per hour for each full year of his age. This basically says that he gets a dollar for each year of his age. So if he is
dollars per hour for each full year of his age. This basically says that he gets a dollar for each year of his age. So if he is  years old, he gets
years old, he gets dollars a day. We also know that he worked
dollars a day. We also know that he worked  days and earned
days and earned  dollars. If he was
dollars. If he was  years old at the beginning of his working period, he would have earned
years old at the beginning of his working period, he would have earned  dollars. If he was
dollars. If he was  years old at the beginning of his working period, he would have earned
years old at the beginning of his working period, he would have earned  dollars. Because he earned
dollars. Because he earned  dollars, we know that he was
dollars, we know that he was  for some period of time, but not the whole time, because then the money earned would be greater than or equal to
for some period of time, but not the whole time, because then the money earned would be greater than or equal to  . This is why he was
. This is why he was  when he began, but turned
when he began, but turned  sometime in the middle and earned
sometime in the middle and earned  dollars in total. So the answer is
dollars in total. So the answer is  .The answer is
.The answer is  . We could find out for how long he was
. We could find out for how long he was  and
and  .
.  . Then
. Then  is
is  and we know that he was
and we know that he was  for
for  days, and
days, and  for
for  days. Thus, the answer is
days. Thus, the answer is  .
.  is at most
is at most  , so
, so  is at most
is at most  . The minimum value of
. The minimum value of  is
is  . However, the only palindrome between
. However, the only palindrome between  and
and  is
is  , which means that
, which means that  must be
must be  .It follows that
.It follows that  is
is  , so the sum of the digits is
, so the sum of the digits is  .
.
 There are
There are  days in a non-leap year. There are
days in a non-leap year. There are  days in a week. Since
days in a week. Since  (or
(or  is congruent to
is congruent to  ), the same date (after February) moves "forward" one day in the subsequent year, if that year is not a leap year.For example:
), the same date (after February) moves "forward" one day in the subsequent year, if that year is not a leap year.For example: Tue
Tue WedHowever, a leap year has
WedHowever, a leap year has  days, and
days, and  . So the same date (after February) moves "forward" two days in the subsequent year, if that year is a leap year.For example:
. So the same date (after February) moves "forward" two days in the subsequent year, if that year is a leap year.For example:  Fri
Fri SunYou can keep count forward to find that the first time this date falls on a Saturday is in
SunYou can keep count forward to find that the first time this date falls on a Saturday is in  :
: Mon
Mon
 Tue
Tue Wed
Wed Fri
Fri Sat
Sat- Since we are given the range of the solutions, we must re-write the inequalities so that we have
 in terms of
in terms of  and
and  .
. Subtract
Subtract  from all of the quantities:
from all of the quantities: Divide all of the quantities by
Divide all of the quantities by  .
. Since we have the range of the solutions, we can make them equal to
Since we have the range of the solutions, we can make them equal to  .
. Multiply both sides by 2.
Multiply both sides by 2.
Re-write without using parentheses.

Simplify.

We need to find
 for the problem, so the answer is
for the problem, so the answer is 
- The water tower holds
 times more water than Logan's miniature. The volume of a sphere is:
times more water than Logan's miniature. The volume of a sphere is:  . Since we are comparing the heights (m), we should compare the radii (m) to find the ratio. Since, the radius is cubed, Logan should make his tower
. Since we are comparing the heights (m), we should compare the radii (m) to find the ratio. Since, the radius is cubed, Logan should make his tower ![$sqrt[3]{1000000} = 100$](http://latex.artofproblemsolving.com/7/0/5/7059c25b41a49aadf0f433430eb36aeb9ce89dc2.png) times shorter than the actual tower. This is
times shorter than the actual tower. This is  meters high, or choice
meters high, or choice  .Note: The fact that
.Note: The fact that  doesn't matter since only the ratios are important.
doesn't matter since only the ratios are important. - The answer is
 because she drove at
because she drove at  kmh for
kmh for  hours (the amount of time before the stop), and 100 kmh for
hours (the amount of time before the stop), and 100 kmh for  because she wasn't driving for
because she wasn't driving for  minutes, or
minutes, or  hours. Multiplying by
hours. Multiplying by  gives the total distance, which is
gives the total distance, which is  kms. Therefore, the answer is
kms. Therefore, the answer is 



![[asy] pair A,B,C,D,E,F,G,H; G=(0,10); A=(0,3.464); B=(6,0); C=(0,0); draw(A--B--C--cycle); F=(1,1.73); E=(2,0); draw(C--F--E); D=(1.5,2.6); draw(C--D); label("$A$",A,W); label("$B$",B,S); label("$C$",C,S); label("$F$",F,N); label("$D$",D,NE); label("$E$",E,S); draw(A--E); draw(anglemark(E,A,B)); draw(anglemark(D,C,A)); [/asy]](http://latex.artofproblemsolving.com/e/8/4/e84f838a57b4720e691a786fee5357d996730f4b.png) Let
Let  .
. Since
Since  ,
, 
- We can begin by first looking at Chris and LeRoy.Suppose Chris and LeRoy are the same species. If Chris is a toad, then what he says is true, so LeRoy is a frog. However, if LeRoy is a frog, then he is lying, but clearly Chris is not a frog, and we have a contradiction. The same applies if Chris is a frog.Clearly, Chris and LeRoy are different species, and so we have at least
 frog out of the two of them.Now suppose Mike is a toad. Then what he says is true because we already have
frog out of the two of them.Now suppose Mike is a toad. Then what he says is true because we already have  toads. However, if Brian is a frog, then he is lying, yet his statement is true, a contradiction. If Brian is a toad, then what he says is true, but once again it conflicts with his statement, resulting in contradiction.Therefore, Mike must be a frog. His statement must be false, which means that there is at most
toads. However, if Brian is a frog, then he is lying, yet his statement is true, a contradiction. If Brian is a toad, then what he says is true, but once again it conflicts with his statement, resulting in contradiction.Therefore, Mike must be a frog. His statement must be false, which means that there is at most  toad. Since either Chris or LeRoy is already a toad, Brian must be a frog. We can also verify that his statement is indeed false.Both Mike and Brian are frogs, and one of either Chris or LeRoy is a frog, so we have
toad. Since either Chris or LeRoy is already a toad, Brian must be a frog. We can also verify that his statement is indeed false.Both Mike and Brian are frogs, and one of either Chris or LeRoy is a frog, so we have  frogs total.
frogs total. 
![[asy] pair A,B,C,D; C=(0,0); B=(4,0); A=(3,1); D=(2,0.666); draw(A--B--C--cycle); draw(B--D); label("$A$",A,N); label("$B$",B,S); label("$C$",C,S); label("$D$",D,NW); label("$3$",A--D,N); label("$8$",C--D,N); [/asy]](http://latex.artofproblemsolving.com/4/6/6/4661024a902bb549ef50c3798e944b3d178a7c4c.png) By the Angle Bisector Theorem, we know that
By the Angle Bisector Theorem, we know that  . If we use the lowest possible integer values for AB and BC (the measures of AD and DC, respectively), then
. If we use the lowest possible integer values for AB and BC (the measures of AD and DC, respectively), then  , contradicting the Triangle Inequality. If we use the next lowest values (
, contradicting the Triangle Inequality. If we use the next lowest values ( and
and  ), the Triangle Inequality is satisfied. Therefore, our answer is
), the Triangle Inequality is satisfied. Therefore, our answer is  , or choice
, or choice  .
.- Imagine making the cuts one at a time. The first cut removes a box
 . The second cut removes two boxes, each of dimensions
. The second cut removes two boxes, each of dimensions  , and the third cut does the same as the second cut, on the last two faces. Hence the total volume of all cuts is
, and the third cut does the same as the second cut, on the last two faces. Hence the total volume of all cuts is  .Therefore the volume of the rest of the cube is
.Therefore the volume of the rest of the cube is  .
. - We can solve this by breaking the problem down into
 cases and adding up the probabilities.Case
cases and adding up the probabilities.Case  : Bernardo picks
: Bernardo picks  . If Bernardo picks a
. If Bernardo picks a  then it is guaranteed that his number will be larger than Silvia's. The probability that he will pick a
then it is guaranteed that his number will be larger than Silvia's. The probability that he will pick a  is
is  .Case
.Case  : Bernardo does not pick
: Bernardo does not pick  . Since the chance of Bernardo picking
. Since the chance of Bernardo picking  is
is  , the probability of not picking
, the probability of not picking  is
is  .If Bernardo does not pick 9, then he can pick any number from
.If Bernardo does not pick 9, then he can pick any number from  to
to  . Since Bernardo is picking from the same set of numbers as Silvia, the probability that Bernardo's number is larger is equal to the probability that Silvia's number is larger.Ignoring the
. Since Bernardo is picking from the same set of numbers as Silvia, the probability that Bernardo's number is larger is equal to the probability that Silvia's number is larger.Ignoring the  for now, the probability that they will pick the same number is the number of ways to pick Bernardo's 3 numbers divided by the number of ways to pick any 3 numbers.We get this probability to be
for now, the probability that they will pick the same number is the number of ways to pick Bernardo's 3 numbers divided by the number of ways to pick any 3 numbers.We get this probability to be  Probability of Bernardo's number being greater is
Probability of Bernardo's number being greater is![[frac{1-frac{1}{56}}{2} = frac{55}{112}]](http://latex.artofproblemsolving.com/9/e/0/9e095b4556f12a1fed7a67640f70ef1dfb484c81.png) Factoring the fact that Bernardo could've picked a
Factoring the fact that Bernardo could've picked a  but didn't:
but didn't:![[frac{2}{3}cdot{frac{55}{112}} = frac{55}{168}]](http://latex.artofproblemsolving.com/f/5/8/f580315e15f0e8bb88ee8d7b2d8109a57b25dd94.png) Adding up the two cases we get
Adding up the two cases we get 
- It is clear that
 is an equilateral triangle. From the Law of Cosines on triangle ABC, we get that
is an equilateral triangle. From the Law of Cosines on triangle ABC, we get that  . Therefore, the area of
. Therefore, the area of  is
is  .If we extend
.If we extend  ,
,  and
and  so that
so that  and
and  meet at
meet at  ,
,  and
and  meet at
meet at  , and
, and  and
and  meet at
meet at  , we find that hexagon
, we find that hexagon  is formed by taking equilateral triangle
is formed by taking equilateral triangle  of side length
of side length  and removing three equilateral triangles,
and removing three equilateral triangles,  ,
,  and
and , of side length
, of side length  . The area of
. The area of  is therefore
is therefore .Based on the initial conditions,
.Based on the initial conditions,![[frac{sqrt{3}}{4}(r^2+r+1) = frac{7}{10}left(frac{sqrt{3}}{4}right)(r^2+4r+1)]](http://latex.artofproblemsolving.com/d/c/1/dc1cb478fd6f41e7cf54668851df87469a184d56.png) Simplifying this gives us
Simplifying this gives us  . By Vieta's Formulas (or Girard identities, or Newton-Girard identities) we know that the sum of the possible value of
. By Vieta's Formulas (or Girard identities, or Newton-Girard identities) we know that the sum of the possible value of  is
is  .
. - The distance of an interior diagonal in this cube is
 and the distance of a diagonal on one of the square faces is
and the distance of a diagonal on one of the square faces is  . It is not possible for the fly to travel any interior diagonal twice, as then it would visit a corner more than once. So, the final sum can have at most
. It is not possible for the fly to travel any interior diagonal twice, as then it would visit a corner more than once. So, the final sum can have at most  as the coefficient of
as the coefficient of  . The other 4 paths taken can be across a diagonal on one of the faces (try to find a such path!), so the maximum distance traveled is
. The other 4 paths taken can be across a diagonal on one of the faces (try to find a such path!), so the maximum distance traveled is  .
. - By Vieta's Formulas, we know that
 is the sum of the three roots of the polynomial
is the sum of the three roots of the polynomial  . Again Vieta's Formulas tells us that
. Again Vieta's Formulas tells us that  is the product of the three integer roots. Also,
is the product of the three integer roots. Also,  factors into
factors into  . But, since there are only three roots to the polynomial, two of the four prime factors must be multiplied so that we are left with three roots. To minimize
. But, since there are only three roots to the polynomial, two of the four prime factors must be multiplied so that we are left with three roots. To minimize  ,
,  and
and  should be multiplied, which means
should be multiplied, which means  will be
will be  and the answer is
and the answer is  .
. - To choose a chord, we know that two points must be chosen. This implies that for three chords to create a triangle and not intersect at a single point, six points need to be chosen. We also know that for any six points we pick, there is only 1 way to connect the chords such that a triangle is formed in the circle's interior. Therefore, the answer is
 , which is equivalent to
, which is equivalent to  .
. - The probability of drawing a white marble from box
 is
is  . The probability of drawing a red marble from box
. The probability of drawing a red marble from box  is
is  .The probability of drawing a red marble at box
.The probability of drawing a red marble at box  is therefore
is therefore

 It is then easy to see that the lowest integer value of
It is then easy to see that the lowest integer value of  that satisfies the inequality is
that satisfies the inequality is  .An easy way to know that
.An easy way to know that  is the answer is that 50*51=2550, so you know n<50 - the only solution for n under 50 is 45.
is the answer is that 50*51=2550, so you know n<50 - the only solution for n under 50 is 45. - We will use the fact that for any integer
 ,
,![begin{align*}(5n+1)(5n+2)(5n+3)(5n+4)&=[(5n+4)(5n+1)][(5n+2)(5n+3)] &=(25n^2+25n+4)(25n^2+25n+6)equiv 4cdot 6 &=24pmod{25}equiv -1pmod{25}.end{align*}](http://latex.artofproblemsolving.com/d/a/d/dada193a2f8d7b846a57fc8ae2fc2e882aeaca4e.png) First, we find that the number of factors of
First, we find that the number of factors of  in
in  is equal to
is equal to  . Let
. Let  . The
. The  we want is therefore the last two digits of
we want is therefore the last two digits of  , or
, or  . Since there is clearly an excess of factors of 2, we know that
. Since there is clearly an excess of factors of 2, we know that  , so it remains to find
, so it remains to find  .We can write
.We can write  as
as  where
where![[M=1cdot 2cdot 3cdot 4cdot 1cdot 6cdot 7cdot 8cdot 9cdot 2cdots 89cdot 18 = frac{90!}{5^{21}},]](http://latex.artofproblemsolving.com/a/b/4/ab48cb8cc1f1c0a9388cd1460aeeeb4aeb038758.png) where every number in the form
where every number in the form  is replaced by
is replaced by  .The number
.The number  can be grouped as follows:
can be grouped as follows: Hence, we can reduce
Hence, we can reduce  to
to Using the fact that
Using the fact that  ,we can deduce that
,we can deduce that  . Therefore
. Therefore  .Finally, combining with the fact that
.Finally, combining with the fact that  yields
yields  .
. - We can find the answer by working backwards. We begin with
 on the bottom row, then the
on the bottom row, then the  goes to the right of the equal's sign in the row above. We find the smallest value
goes to the right of the equal's sign in the row above. We find the smallest value  for which
for which  and
and  , which is
, which is  .We repeat the same procedure except with
.We repeat the same procedure except with  for the next row and
for the next row and  for the row after that. However, at the fourth row, we see that solving
for the row after that. However, at the fourth row, we see that solving  yields
yields  , in which case it would be incorrect since
, in which case it would be incorrect since  is not the greatest perfect square less than or equal to
is not the greatest perfect square less than or equal to . So we make it a
. So we make it a  and solve
and solve  . We continue on using this same method where we increase the perfect square until
. We continue on using this same method where we increase the perfect square until  can be made bigger than it. When we repeat this until we have
can be made bigger than it. When we repeat this until we have  rows, we get:
rows, we get:![[begin{array}{ccccc}{}&{}&{}&{}&7223 7223&-&84^{2}&=&167 167&-&12^{2}&=&23 23&-&4^{2}&=&7 7&-&2^{2}&=&3 3&-&1^{2}&=&2 2&-&1^{2}&=&1 1&-&1^{2}&=&0 end{array}]](http://latex.artofproblemsolving.com/8/a/c/8acd99dc227327e964c7e0b92b1319c372a9e983.png) Hence the solution is the last digit of
Hence the solution is the last digit of 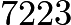 , which is
, which is  .Note: We can go up to
.Note: We can go up to  , and then notice the pattern of units digits alternating between
, and then notice the pattern of units digits alternating between  and
and , so we do not need to calculate
, so we do not need to calculate 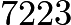 .
.
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





