- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Further Maths: Core Pure:复习笔记3.1.1 Roots of Polynomials
Roots of Quadratics
How are the roots of a quadratic linked to its coefficients?
- Because a quadratic equation
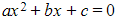 (where
(where 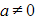 ) has roots
) has roots 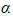 and
and 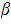 , you can write this equation instead in the form
, you can write this equation instead in the form 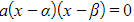
-
- Note that

- It is possible that the roots are repeated, i.e. that
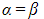
- Note that
- You can then equate the two forms:
- Then (because
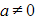 ) you can divide both sides of that by a and expand the brackets:
) you can divide both sides of that by a and expand the brackets:
-
-
- Finally, compare the coefficients
- Coefficients of x:
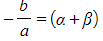
- Constant terms:
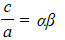
- Coefficients of x:
- Finally, compare the coefficients
- Therefore for a quadratic equation
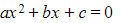 :
:
-
- The sum of the roots
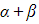 is equal to
is equal to 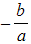
- The product of the roots
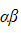 is equal to
is equal to 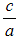
- Unless an exam question specifically asks you to prove these results, you can always use them without proof to answer questions about quadratics
- The sum of the roots
Related Roots
- You may be asked to consider two quadratic equations, with the roots of the second quadratic linked to the roots of the first quadratic in some way
-
- You are usually required to find the sum or product of the roots of the second equation
- The strategy is to use identities which contain
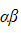 and
and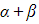 (where
(where 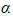 and
and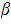 are the roots of the first quadratic)
are the roots of the first quadratic)
-
- If you know the values of
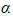 and
and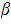 from the first quadratic, you can use them to help find the sum or product of the new roots
from the first quadratic, you can use them to help find the sum or product of the new roots - If the second quadratic has roots
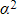 and
and 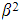 , then use the identities:
, then use the identities:
- If you know the values of
-
- If the second quadratic has roots
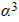 and
and 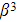 , then use the identities:
, then use the identities:
- If the second quadratic has roots
-
- If the second quadratic has roots
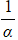 and
and 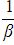 , then use the identities:
, then use the identities:
- If the second quadratic has roots
- You can then form a new equation for a quadratic with the new roots
- This is done by recalling that a quadratic with a given pair of roots can be written in the form x2 – (sum of the roots)x + (product of the roots) = 0
- Be aware that this will not give a unique answer
- This is because multiplying an entire quadratic by a constant does not change its roots
- You can use this fact, for example, to find a quadratic that has a particular pair of roots AND has all integer coefficients
- See the worked example below for an example of how to do some of this!
Worked Example
The roots of an equation ![]() are
are ![]() and
and ![]() .
.
a) Find integer values of a, b, and c.
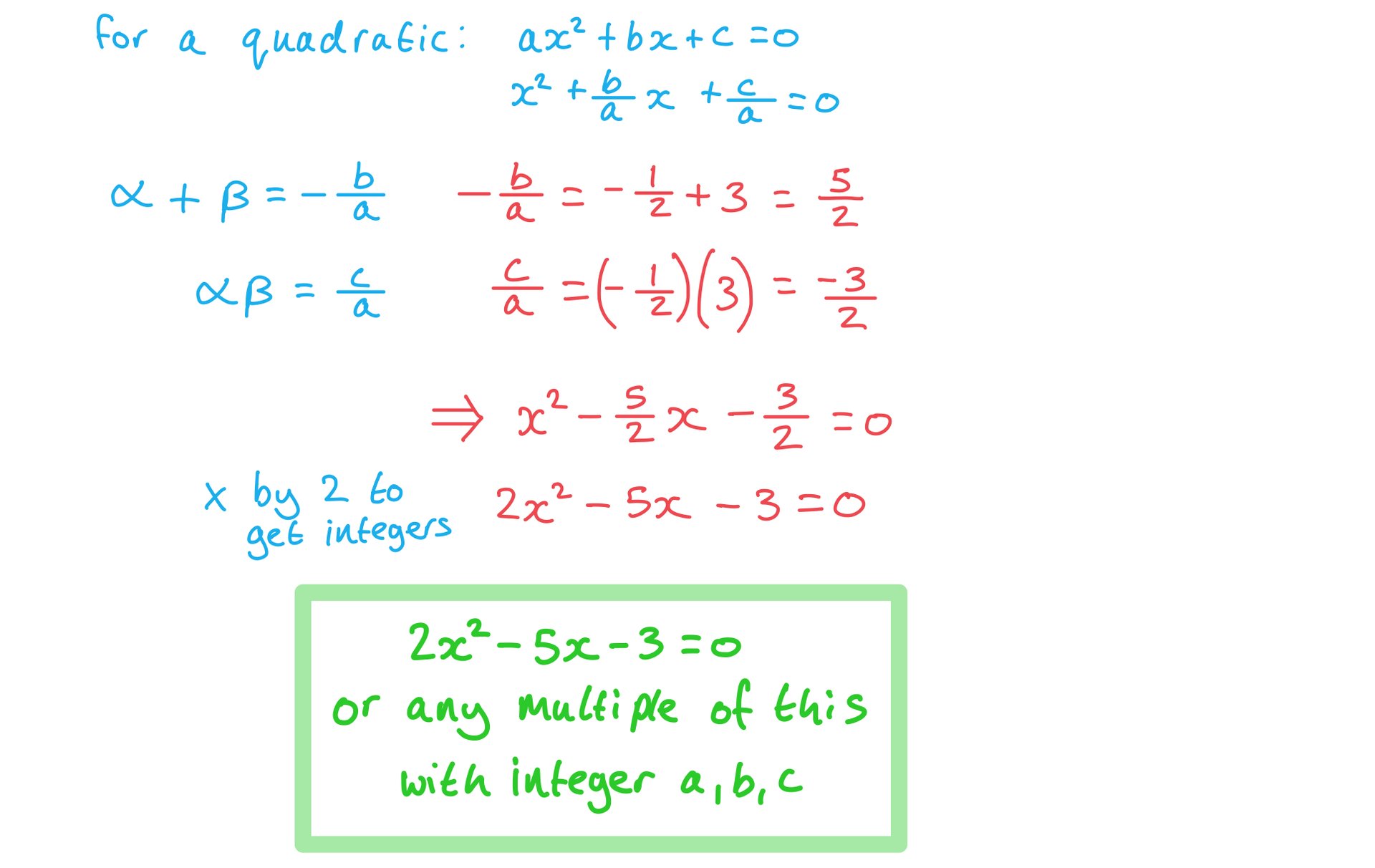
b) Hence find a quadratic equation whose roots are 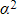 and
and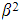 .
.
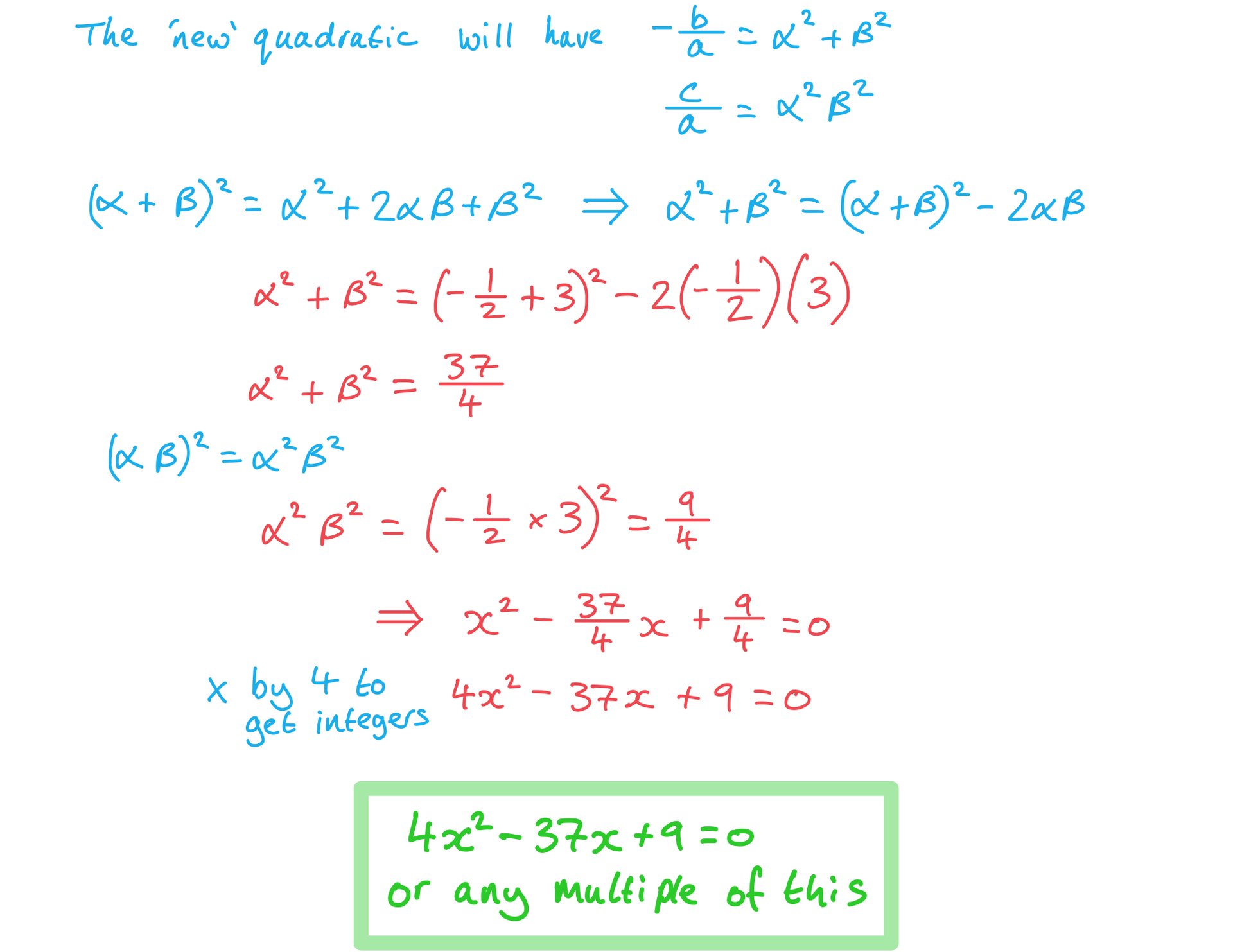
Roots of Cubics
How are the roots of a cubic linked to its coefficients?
- Because a cubic equation
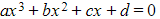 (where
(where 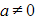 ) has roots α, β and
) has roots α, β and 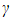 , you can write this equation instead in the form
, you can write this equation instead in the form 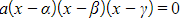
-
-
- Note that
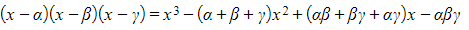
- It is possible that some of the roots are repeated, i.e. that some or all of them are equal to each other
- Note that
-
-
- You can then equate the two forms:
- Then (because
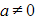 ) you can divide both sides of that by a and expand the brackets:
) you can divide both sides of that by a and expand the brackets:
- Finally, compare the coefficients
- Coefficients of x2:
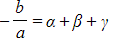
- Coefficients of x:
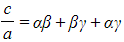
- Constant terms:
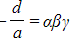
- Coefficients of x2:
- You can then equate the two forms:
- Therefore for a cubic equation
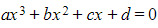 :
:
-
- The sum of the roots
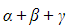 is equal to
is equal to 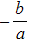
- The sum of roots
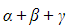 can also be denoted by
can also be denoted by 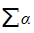
- The sum of roots
- The sum of the product pairs of roots
 is equal to
is equal to 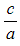
- This ‘sum of pairs’
 can also be denoted by
can also be denoted by 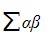
- This ‘sum of pairs’
- The product of the roots
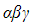 is equal to
is equal to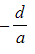
- The product of roots
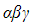 can also be denoted by
can also be denoted by 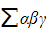
- See quartic equations where using this ‘sum of triples’ notation makes more sense!
- The product of roots
- Unless an exam question specifically asks you to prove these results, you can always use them without proof to answer questions about cubics
- The sum of the roots
Related Roots
- You may be asked to consider two cubic equations, with the roots of the second cubic linked to the roots of the first cubic in some way
-
- You are usually required to find the sum or product of the roots of the second equation
- The strategy is to use identities which contain
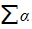 ,
, 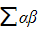 , and
, and 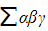 (where α, β and γ are the roots of the first cubic)
(where α, β and γ are the roots of the first cubic)
-
- If you know the values of α, β, and γ from the first cubic, you can use them to help find the sum or product of the new roots
-
- If the second cubic has roots
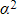 ,
, 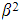 , and
, and  , then use the identities:
, then use the identities:
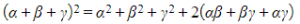
- i.e.,
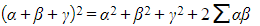
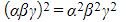
- If the second cubic has roots
-
- If the second cubic has roots
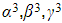 , then use the identities:
, then use the identities:
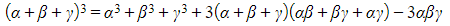
- i.e.,
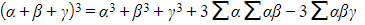
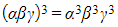
- If the second cubic has roots
-
- If the second cubic has roots
 ,
, 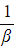 , and
, and 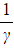 , then use the identities:
, then use the identities:
- If the second cubic has roots
- You can then form a new equation for a cubic with the new roots
- This is done by recalling that a cubic with three given roots can be written in the form
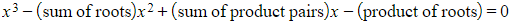
- Be aware that this will not give a unique answer
- This is because multiplying an entire cubic by a constant does not change its roots
- You can use this fact, for example, to find a cubic that has a particular pair of roots AND has all integer coefficients
- This is done by recalling that a cubic with three given roots can be written in the form
Worked Example
a)Given the cubic equation 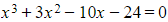 , find
, find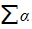 ,
, 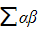 , and
, and 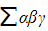
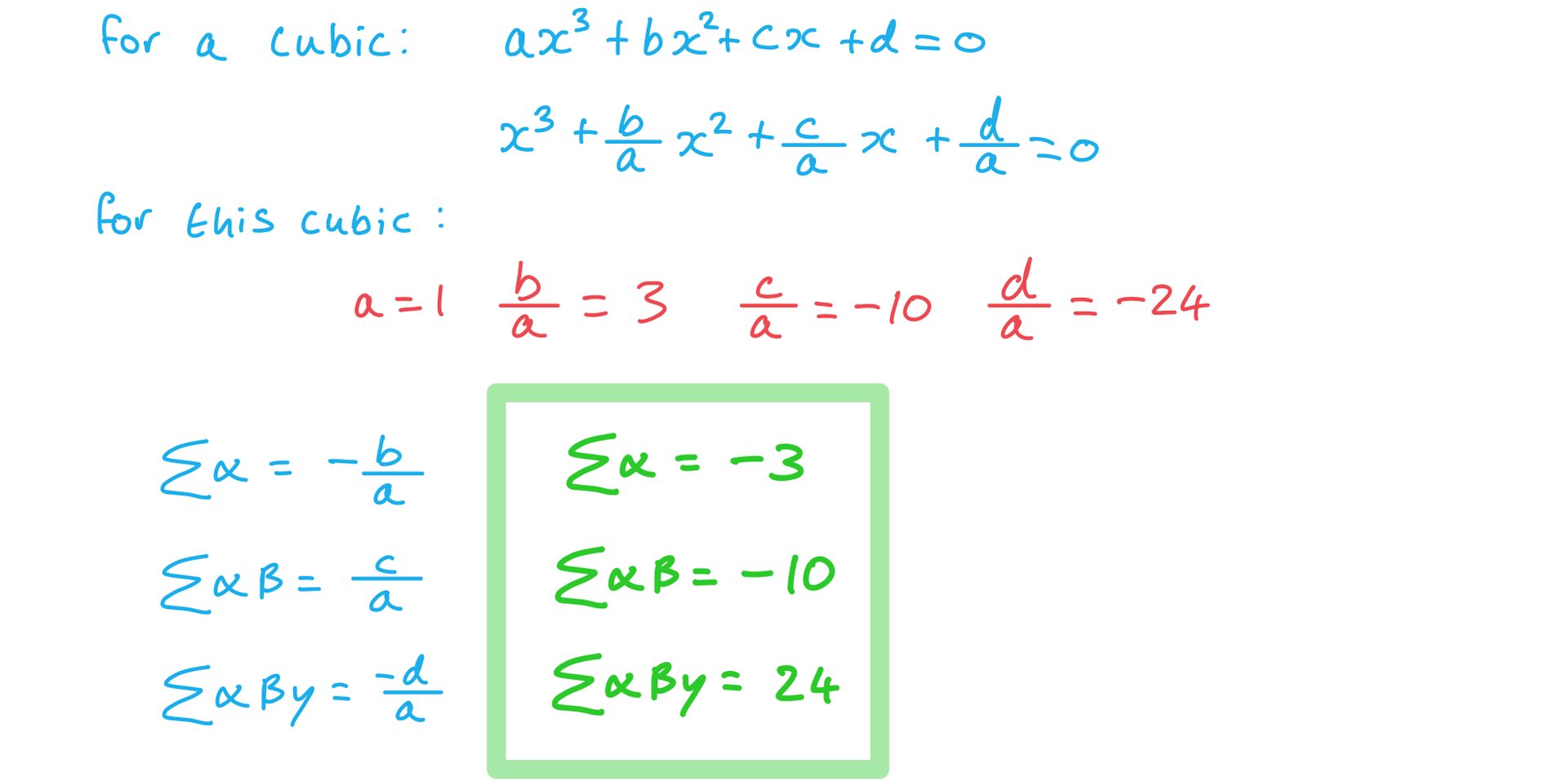
b)Another cubic has roots  ,
,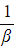 , and
, and 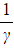 . Find
. Find 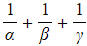 .
.

Roots of Quartics
How are the roots of a quartic linked to its coefficients?


Related Roots
- You may be asked to consider two quartic equations, with the roots of the second quartic linked to the roots of the first quartic in some way
- You are usually required to find the sum or product of the roots of the second equation
- The strategy is to use identities which contain
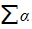 ,
, 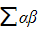 ,
, 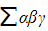 , and
, and 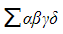 (where α, β,γ and δ are the roots of the first quartic)
(where α, β,γ and δ are the roots of the first quartic)
- If you know the values of α, β, γ, and δ from the first quartic, you can use them to help find the sum or product of the new roots
- If the second quartic has roots
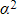 ,
, 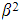 ,
,  and
and 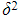 , then use the identities:
, then use the identities:
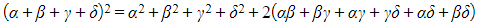
- i.e.,
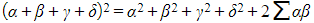
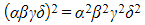
-
- (Note that you will not be asked about a quartic with roots
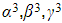 and
and 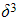 )
) - If the second quartic has roots
 ,
, 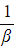 ,
, 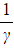 and
and 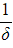 , then use the identities:
, then use the identities:
- (Note that you will not be asked about a quartic with roots
- You can then form a new equation for a quartic with the new roots
- This is done by recalling that a quartic with four given roots can be written in the form
![]()
-
- Be aware that this will not give a unique answer
- This is because multiplying an entire quartic by a constant does not change its roots
- You can use this fact, for example, to find a quartic that has a particular pair of roots AND has all integer coefficients
- Be aware that this will not give a unique answer
Worked Example
a) The roots of 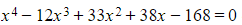 are α、β、γ and δ. Find
are α、β、γ and δ. Find 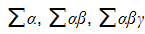 , and
, and 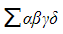 .
.
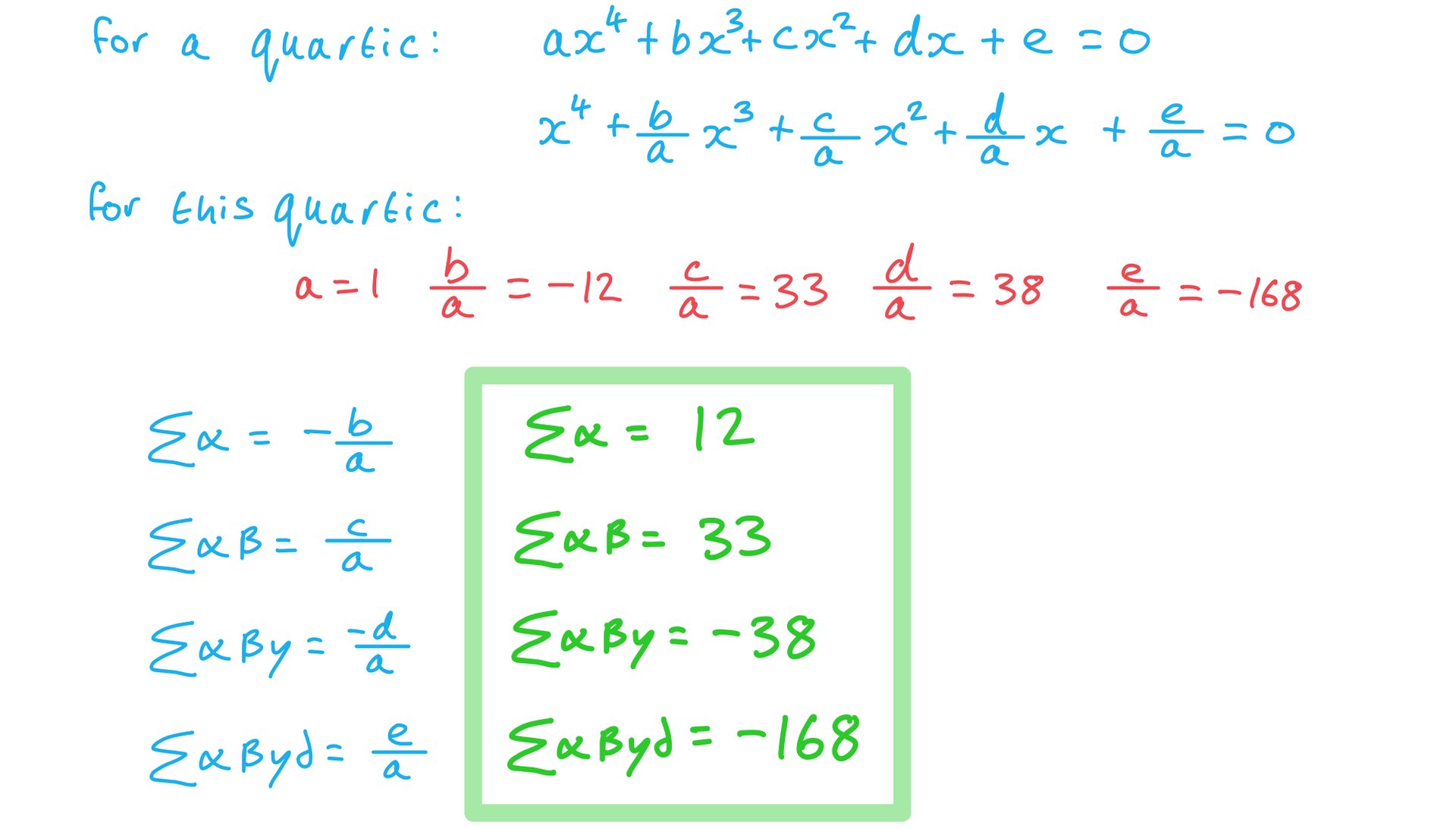
b) Another quartic has roots 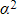 ,
,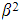 ,
, and
and 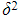 . Find the value of
. Find the value of 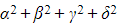 .
.

Roots of Polynomials
What is the general pattern linking the roots to the coefficients of a polynomial?
- By looking at the links between the coefficients and the roots of quadratics, cubics, and quartics, you can see that a pattern emerges, which also holds true for higher order polynomials
- It is useful to use sigma notation to keep expressions for sums of roots concise
- For a quartic with roots
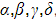 , for example:
, for example:
- The sum of the roots
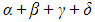 is denoted by
is denoted by 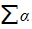
- The sum of the pairs of roots
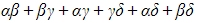 is denoted by
is denoted by 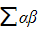
- The sum of the triples of roots
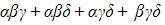 is denoted by
is denoted by 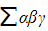
- The sum of the sets of fours (in this case just one term)
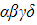 is denoted by
is denoted by 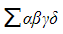
- The sum of the roots
- For a quartic with roots
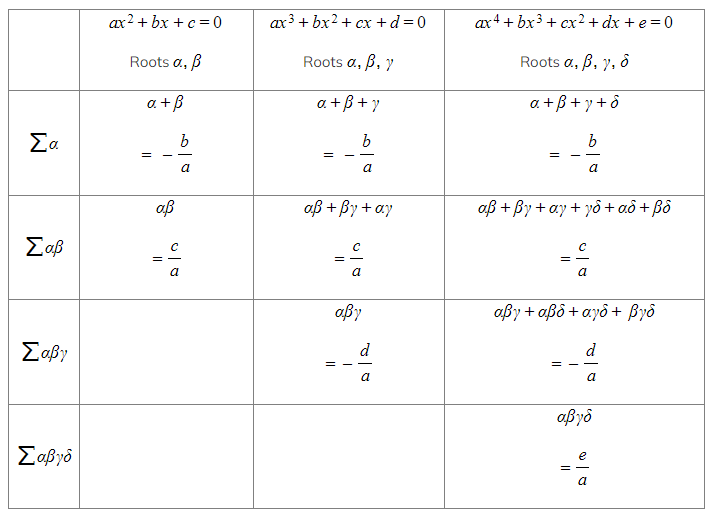
- The table below summarises the relationships between the coefficients and roots of quadratics, cubics, and quartics:
How can I find sums and products of related roots?
- You may be asked to consider a second equation, that has roots linked to the roots of the first equation in some way
- You are usually required to find the sum or product of the roots of the second equation
- The strategy is to use identities containing
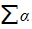 ,
,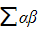 ,
,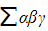 , and/or
, and/or 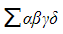 (depending on the question and the degree of the polynomial)
(depending on the question and the degree of the polynomial)
- If you know the value of the roots from the first equation, these identities can help you find the sum or product of the roots of the second equation
- The table below shows useful identities for finding a new quadratic equation whose roots are related to the roots α and β of the original quadratic equation
- In each case the sum or the product of the ‘new roots’ can be linked back to
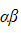 or
or 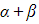 for the original equation
for the original equation
- In each case the sum or the product of the ‘new roots’ can be linked back to

- Similar identities that could be useful for cubics and quartics are listed earlier in this revision note in the cubics and quartics sections
- A good place to start if the new roots are squared, is by considering
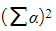
- or if the new roots are cubed, then start by considering
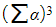
- or if the new roots are reciprocals (i.e.,
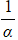 ,
,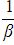 , etc.), then start by adding the new roots together to form a single algebraic fraction
, etc.), then start by adding the new roots together to form a single algebraic fraction
- or if the new roots are cubed, then start by considering
Worked Example
a) Given a polynomial equation of order 5 (a quintic);  , make 5 conjectures linking the coefficients a, b, c, d, e, f to its roots
, make 5 conjectures linking the coefficients a, b, c, d, e, f to its roots 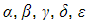 .
.
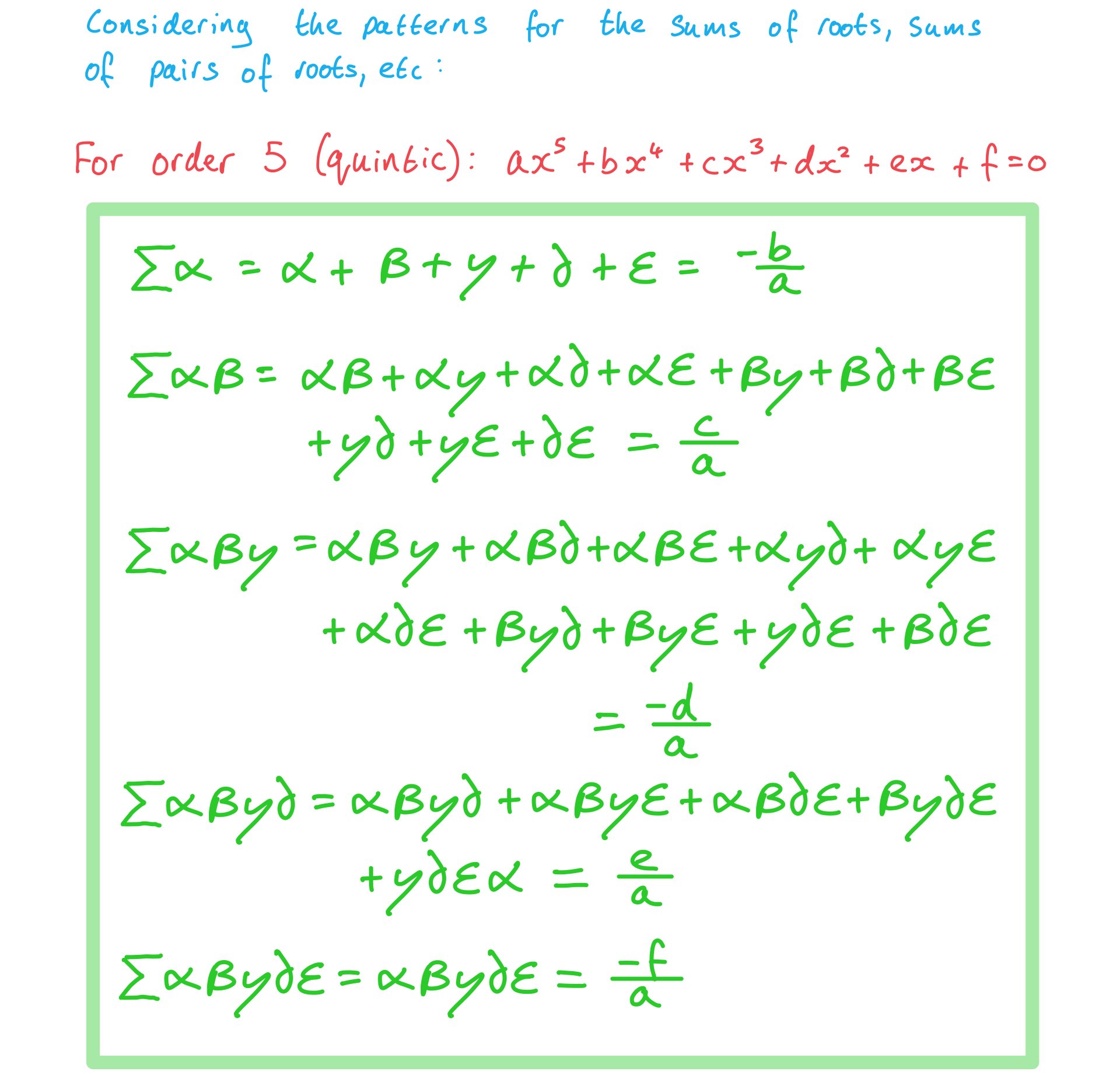
b) Test your conjectures on the example: 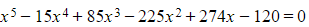 which has roots
which has roots 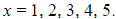 .
.
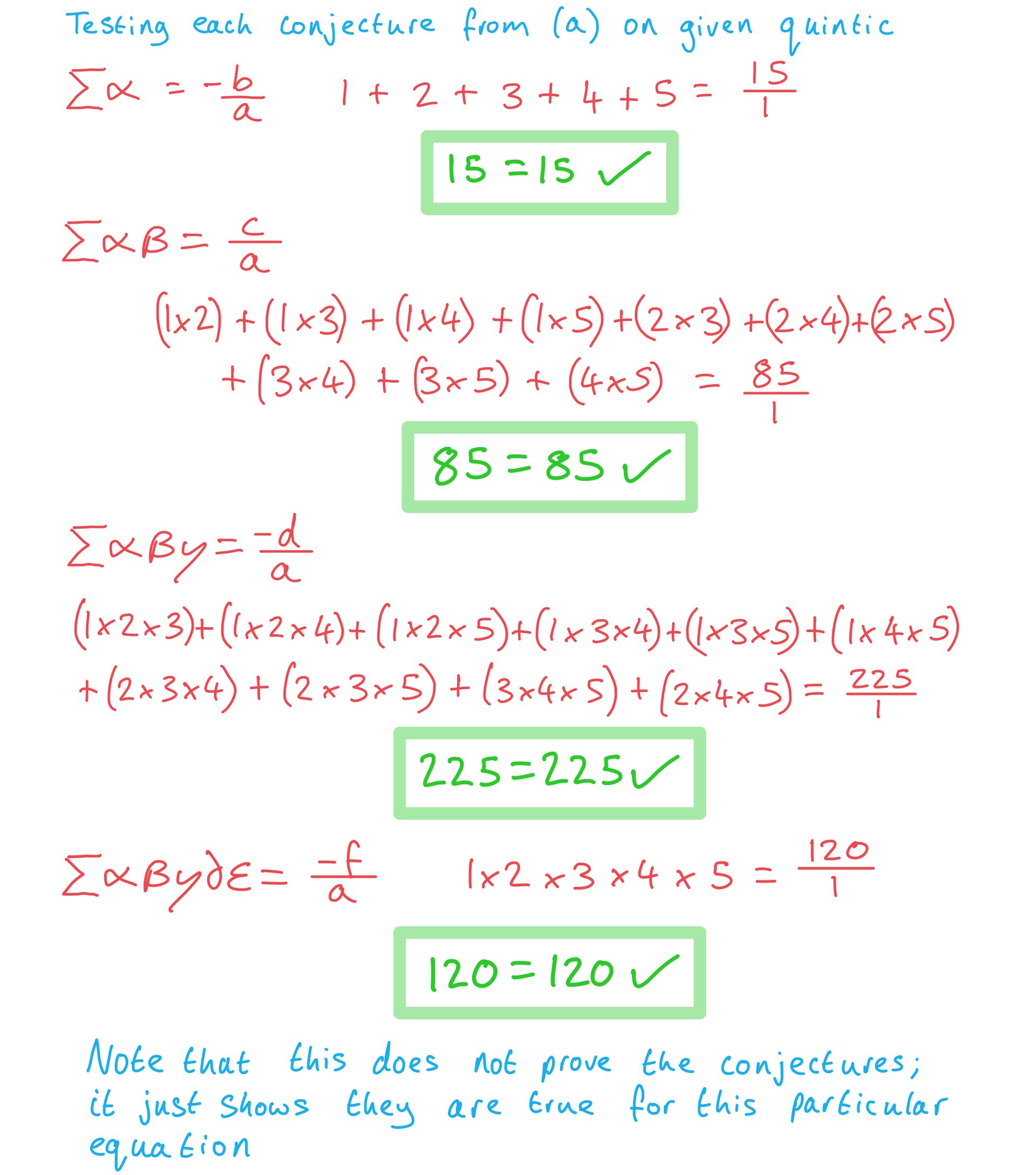
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





