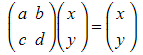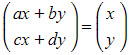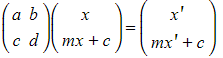- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Further Maths: Core Pure:复习笔记2.2.3 Invariant Points & Lines
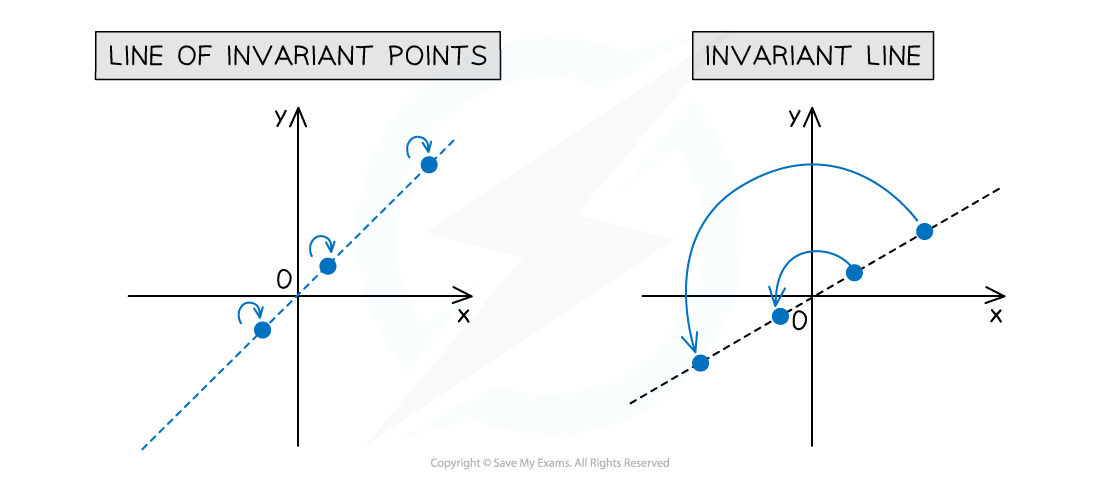
Invariant Points
What is an invariant point?
- When applying transformations to a shape or collection of points, there may be some points that stay in their original position; these are known as invariant points
How can I find invariant points?
- If the point given by position vector
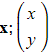 , is invariant under transformation
, is invariant under transformation 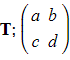 then we can say that
then we can say that 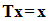
- This will create a system of simultaneous equations which can be solved to find the invariant point
- The origin (0,0) is always invariant under a linear transformation
Exam Tip
- Where the question allows, use your calculator to help solve the simultaneous equations
- Test your found invariant point by multiplying it by the transformation matrix, and making sure you still end up with the same point (invariant)
Worked Example
Find any invariant points under the transformation given by 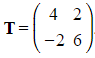 .
.
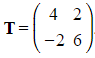 .
. 
A Line of Invariant Points
What is a line of invariant points?
- If every point on a line is mapped to itself under a particular transformation, then it is a line of invariant points
- For example, a line of reflection is a line of invariant points
How can I find a line of invariant points?
- Use the same strategy as for finding a single invariant point:
- If the point given by position vector
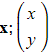 , is invariant under transformation
, is invariant under transformation 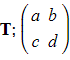 then we can say that
then we can say that 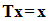
- This will create a system of simultaneous equations which can be solved to find the invariant point(s)
- If the point given by position vector
- If there is a line of invariant points, rather than solving to find a single solution (a point), the two equations will be able to simplify to the same equation
- This means that there are infinitely many solutions, and therefore infinitely many invariant points
- A line contains infinitely many points
- Your solution will be the equation of the invariant line e.g. y=3x
- This means that there are infinitely many solutions, and therefore infinitely many invariant points
Exam Tip
- It may not always be obvious that the two equations reduce to the same thing (they could be an awkward multiple of each other)
- Use your calculator’s simultaneous equation solver; it will tell you that there are infinitely many solutions
Worked Example
Find the equation of the line of invariant points under the transformation given by 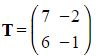

Invariant Lines
What’s the difference between a line of invariant points and an invariant line?
- If every point on a line is mapped to itself under a particular transformation, then it is a line of invariant points
- Every single point on the line must stay in the same place
- With an invariant line however, every point on the line must simply map to another point on the same line
- We are only concerned with the overall line; not the individual points
How do I find an invariant line?
- We can use a similar strategy to finding invariant points, with two slight changes
- Use
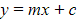 to write the original position vector as
to write the original position vector as 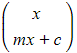
- Write the transformed position vector as
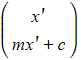 using the same idea
using the same idea
- Notice that the values of m and c will be the same, but different x and y coordinates
- This because it is a different point, on the same line
- Use
- For an invariant line under transformation
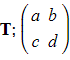 we can write
we can write
- This will create a system of simultaneous equations which can be solved to find the invariant line(s)
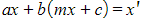
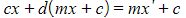
- The first equation can be substituted into the second to give an equation in terms of the variable x and the constants m and c
- This equation can then be solved to find the values of m and c by equating the coefficients of x, and then equating the constant terms
- There may be multiple solutions for m and c if there are multiple invariant lines
Worked Example
Find the equation of any invariant lines under the transformation 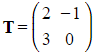

转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1