- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Further Maths: Core Pure:复习笔记2.2.1 Transformations using a Matrix
Transformations using a Matrix
What is a transformation matrix?
- A transformation matrix is used to determine the coordinates of an image from the transformation of an object
- reflections, rotations, enlargements and stretches
- Commonly used transformation matrices include
- (In 2D) a multiplication by any 2x2 matrix could be considered a transformation (in the 2D plane)
- This can be done similarly in higher dimensions
- An individual point in the plane can be represented as a position vector,
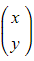
- Several points, that create a shape say, can be written as a position matrix
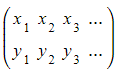
- Several points, that create a shape say, can be written as a position matrix
- A matrix transformation will be of the form
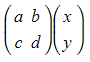
- where
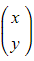 represents any point in the 2D plane
represents any point in the 2D plane 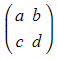 is a given matrix
is a given matrix
- where
How do I find the coordinates of an image under a transformation?
- The coordinates (x’, y’) - the image of the point (x, y) under the transformation with matrix
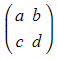 are given by
are given by
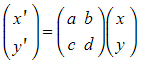
- Similarly, for a position matrix
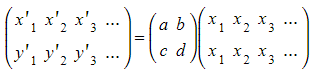
- A calculator can be used for matrix multiplication
- If matrices involved are small, it may be as quick to do this manually
- STEP 1
Determine the transformation matrix (T) and the position matrix (P)
The transformation matrix, if uncommon, will be given in the question
The position matrix is determined from the coordinates involved, it is best to have the coordinates in order, to avoid confusion - STEP 2
Set up and perform the matrix multiplication required to determine the image position matrix, P’
P’ = TP - STEP 3
Determine the coordinates of the image from the image position matrix, P’
How do I find the coordinates of the original point given the image under a transformation?
- To ‘reverse’ a transformation we would need the inverse transformation matrix
- i.e. T-1
- For a 2x2 matrix
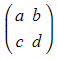 the inverse is given by
the inverse is given by 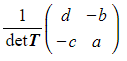
- where
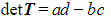
- where
- A calculator can be used to work out inverse matrices
- You would rearrange
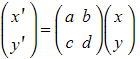
Exam Tip
- Read the question carefully to determine if you have the points before or after a transformation
Worked Example
A quadrilateral, Q, has the four vertices A(2, 5), B(5, 9), C(11, 9) and D(8, 5).
Find the coordinates of the image of Q under the transformation 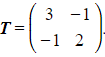

Determinant of a Transformation Matrix
What does the determinant of a transformation matrix (A) represent?
- The absolute value of the determinant of a transformation matrix is the area scale factor (2D) or volume scale factor (3D)
- Area scale factor = |det A| if 2x2
- Volume scale factor = |det A| if 3x3
- The area/volume of the image will be product of the area/volume of the object and |det A|
- Area of image = |det A| × Area of object (if 2x2)
- Volume of image = |det A| × Volume of object (if 3x3)
- Note the area will reduce if |det A| < 1
- If the determinant is negative then the orientation of the shape will be reversed
- For example: the shape has been reflected
How do I solve problems involving the determinant of a transformation matrix?
- Problems may involve comparing areas of objects and images
- This could be as a percentage, proportion, etc
- Missing value(s) from the transformation matrix (and elsewhere) can be deduced if the determinant of the transformation matrix is known
- Remember to use the absolute value of the determinant
- This can lead to multiple answers to equations
- Use your calculator to solve these
Worked Example
An isosceles triangle has vertices A(3, 1), B(15, 1) and C(9, 9).
a) Find the area of the isosceles triangle.
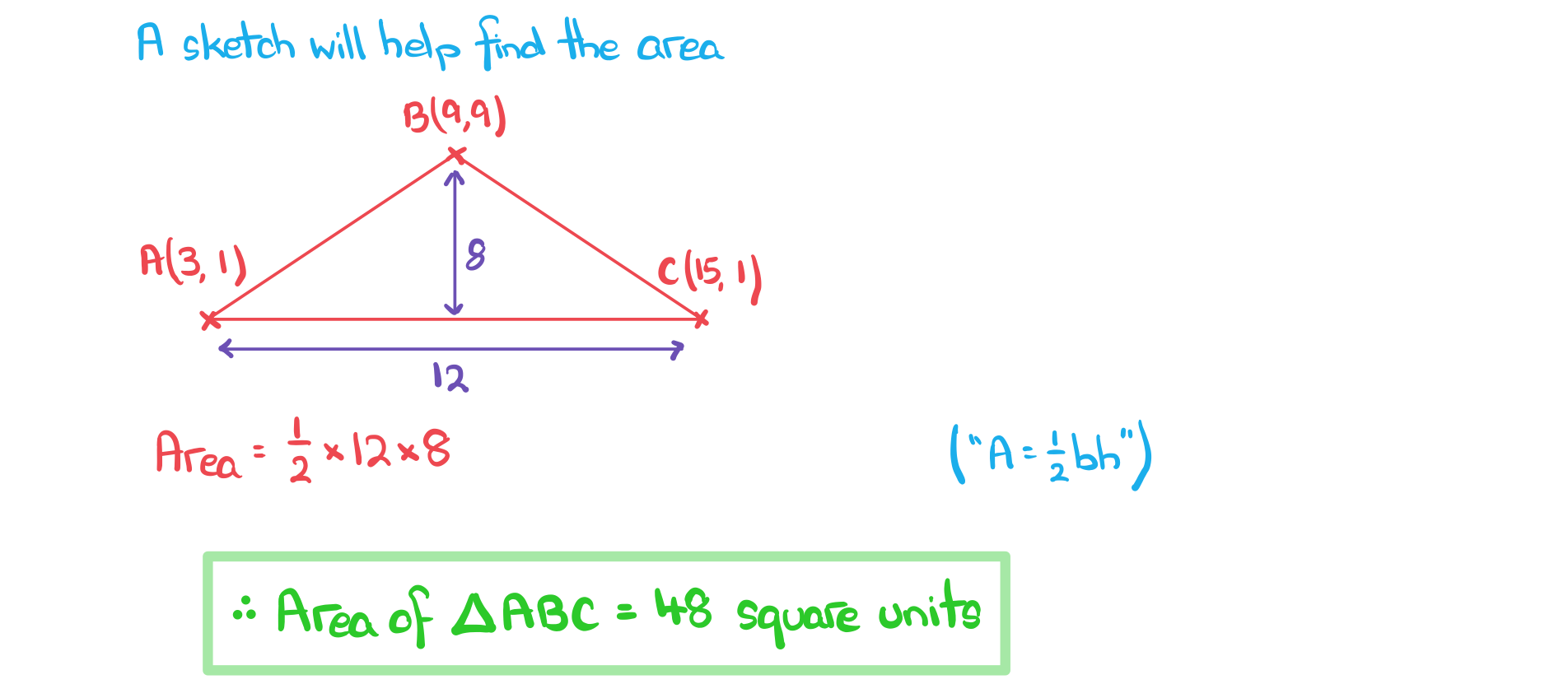
b) Triangle △ABC is transformed using the matrix 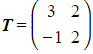 . Find the area of the transformed triangle.
. Find the area of the transformed triangle.
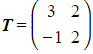 . Find the area of the transformed triangle.
. Find the area of the transformed triangle.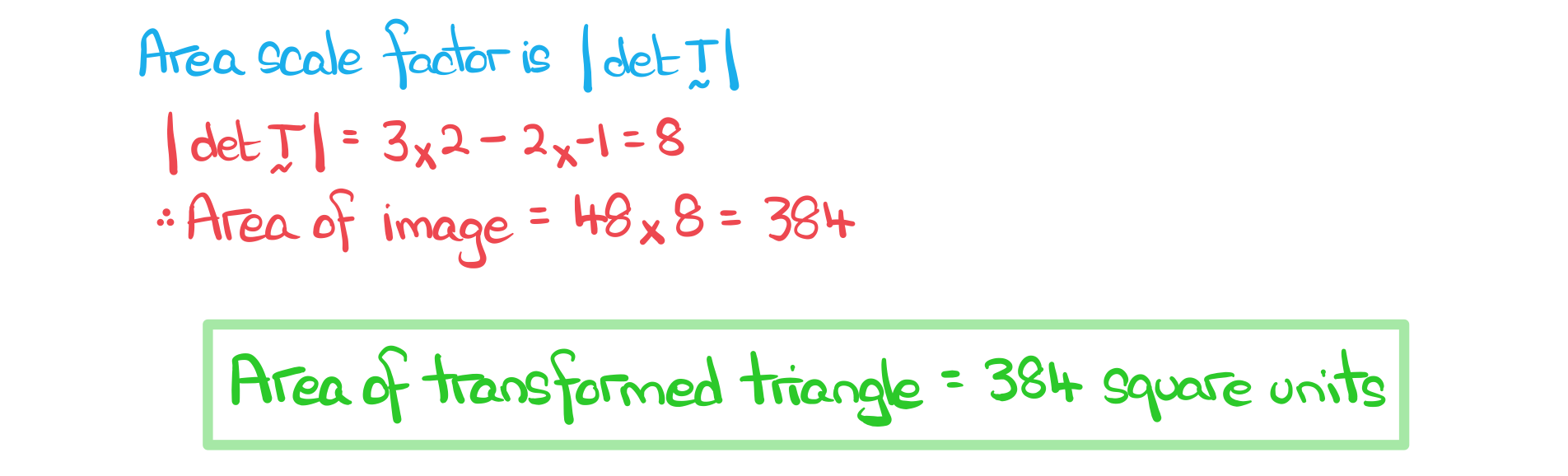
c) Triangle △ABC is now transformed using the matrix 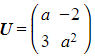 where
where 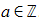 . Given that the area of the image is twice as large as the area of the object, find the value of
. Given that the area of the image is twice as large as the area of the object, find the value of 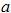 .
.
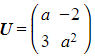 where
where 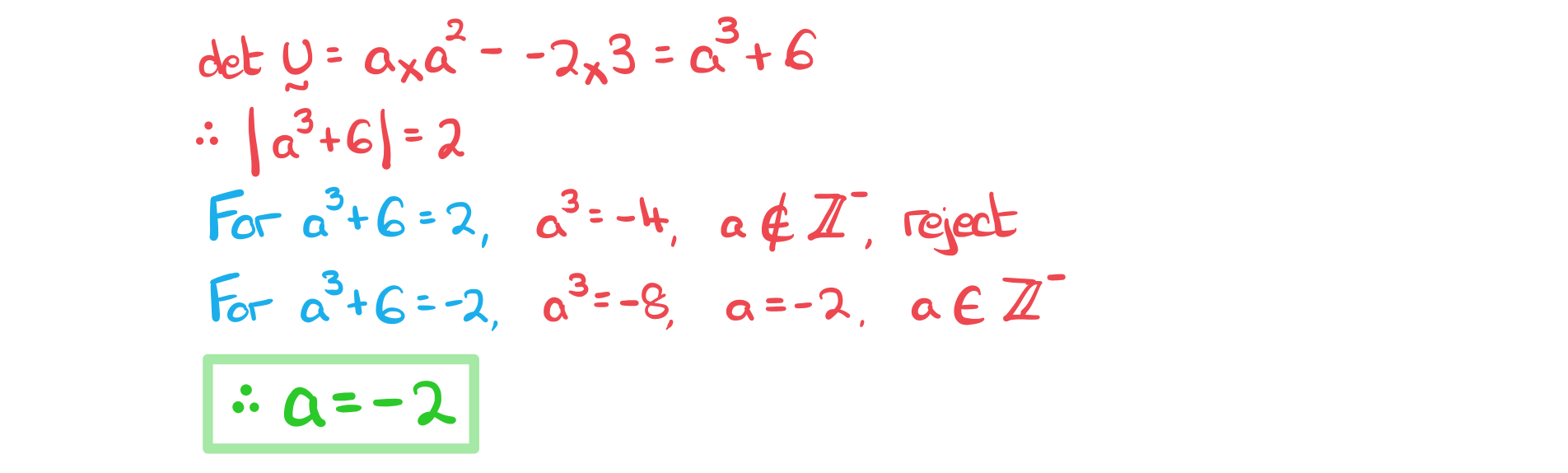
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





