- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Further Maths: Core Pure:复习笔记2.1.3 Inverses of Matrices
Inverse of a Matrix
What is an inverse of a matrix?
- The determinant can be used to find out if a matrix is invertible or not:
- If
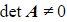 , then
, then 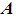 is invertible
is invertible - If
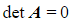 , then
, then 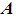 is singular and does not have an inverse
is singular and does not have an inverse
- If
- The inverse of a square matrix
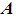 is denoted as the matrix
is denoted as the matrix 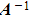
- The product of these matrices is an identity matrix,
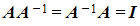
- You can use your calculator to find the inverse of matrices
- You need to know how to find the inverse of 2x2 and 3x3 matrices by hand
- Inverses can be used to rearrange equations with matrices:
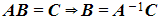 (pre-multiplying by
(pre-multiplying by 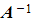 )
)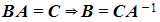 (post-multiplying by
(post-multiplying by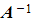 )
)
- The inverse of a product of matrices is the product of the inverse of the matrices in reverse order:
Exam Tip
- Many past exam questions exploit the property
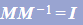
- these typically start with two, seemingly, unconnected matrices
- M and N, say, possibly with some unknown elements
- the result of MN is often a scalar multiple of I, kI say
- so M and N are (almost) inverses of each other
- You are expected to deduce
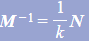
- You are expected to deduce
- Look out for and practise this style of question, they are very common
- these typically start with two, seemingly, unconnected matrices
Worked Example
Consider the matrices 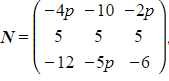 and
and  , where
, where ![]() is a constant.
is a constant.
a) Find 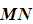 , writing the elements in terms of
, writing the elements in terms of 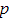 where necessary.
where necessary.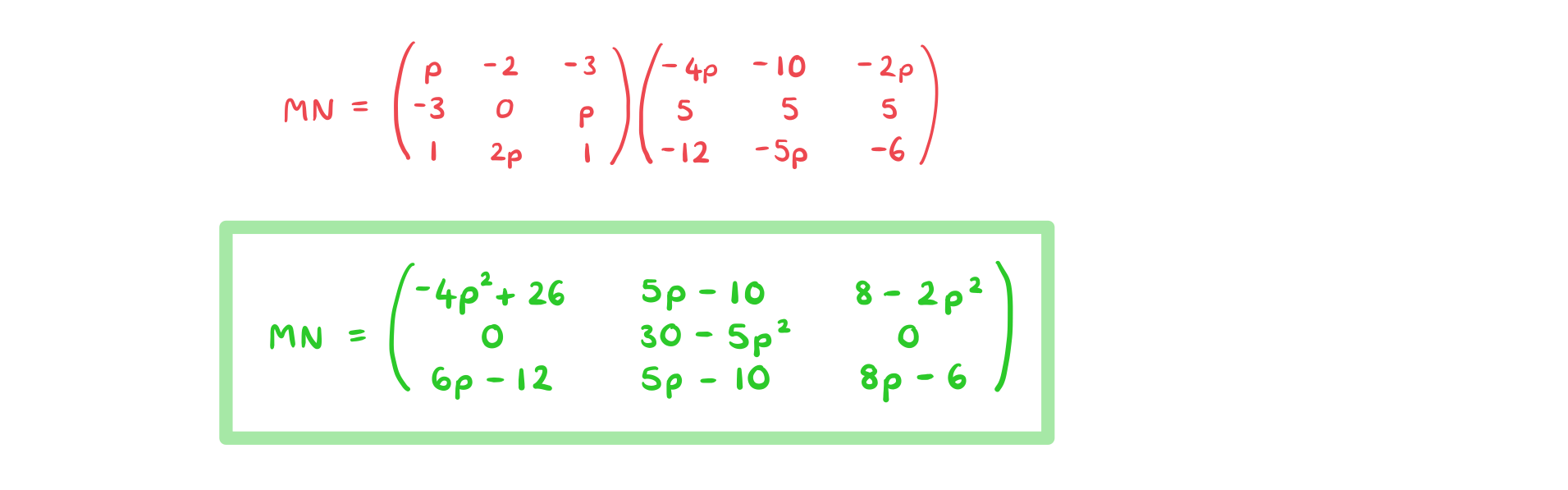

b) In the case  , deduce the matrix
, deduce the matrix 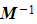 .
. 

Finding the Inverse of a 2x2 Matrix
How do I find the inverse of a 2x2 matrix?
- The method for finding the inverse of a
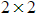 matrix is:
matrix is:
- Switch the two entries on leading diagonal
- Change the signs of the other two entries
- Divide by the determinant
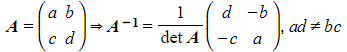
Worked Example
Consider the matrices 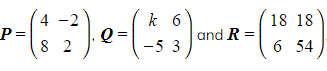 , where
, where ![]() is a constant.
is a constant.
a) Find 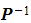 .
.
b) Given that  find the value of
find the value of 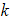 .
.
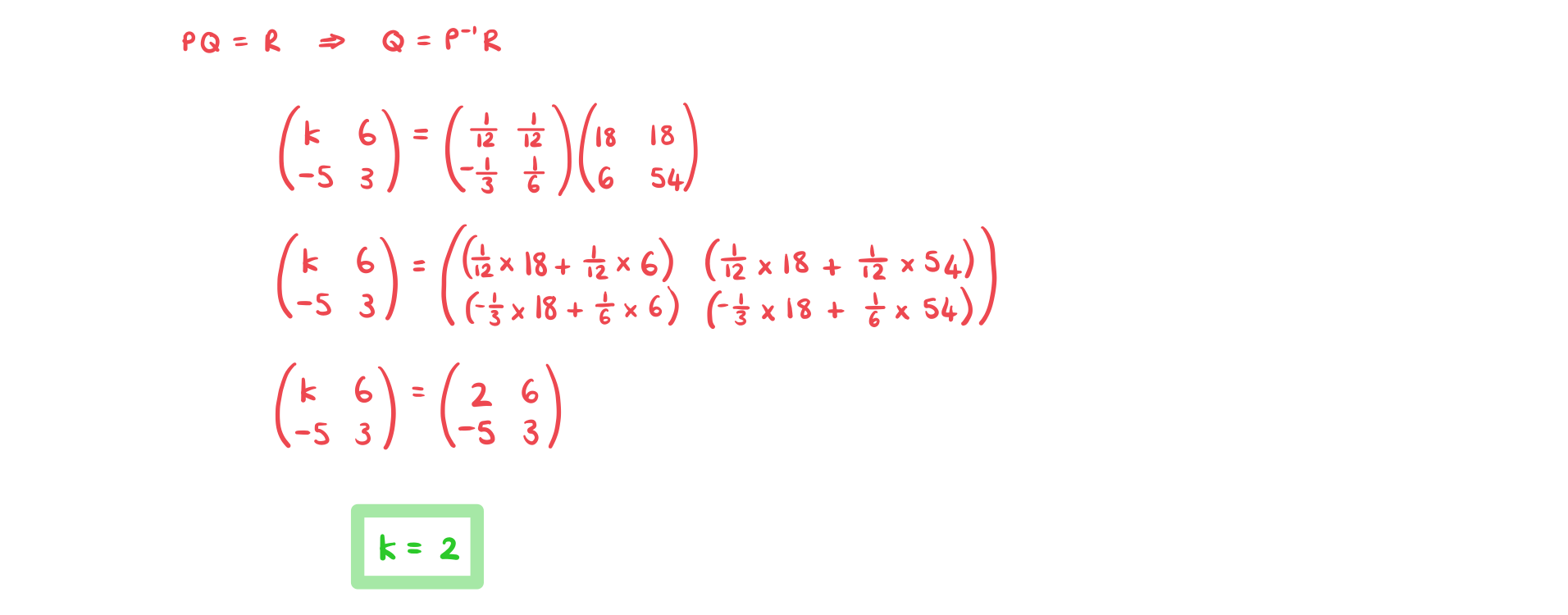
Finding the Inverse of a 3x3 Matrix
How do I find the inverse of a 3x3 matrix?
- This is easiest to see with an example
- Use the matrix
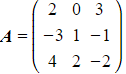
- Use the matrix
- STEP 1
Find the determinant of a 3x3 matrix- The inverse only exists if the determinant is non-zero
- e.g.
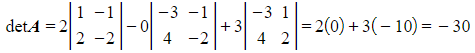
- e.g.
- The inverse only exists if the determinant is non-zero
- STEP 2
Find the minor for every element in the matrix.- You will sometimes see this written as a huge matrix – like below
This is called the matrix of minors and is often denoted by M
With pen and paper, this can get quite large and cumbersome to work with so you may prefer to lay the minors out separately and form M at the end- e.g.
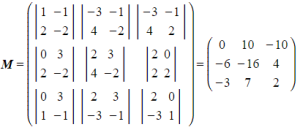
- e.g.
- You will sometimes see this written as a huge matrix – like below
- STEP 3
Find the matrix of cofactors, often denoted by C, by combining the matrix of signs, with the matrix of minors- The matrix of signs is
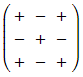
- e.g.
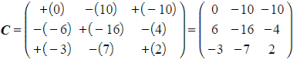
- e.g.
- The matrix of signs is
- STEP 4
Transpose the matrix of cofactors to form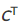
- This is sometimes called the adjugate of A
- e.g.
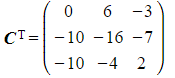
- e.g.
- This is sometimes called the adjugate of A
- STEP 5
Find the inverse of A by dividing CT by the determinant of A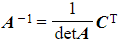
- e.g.
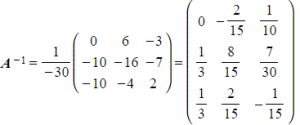
- e.g.
- It is often convenient to leave A-1 as a (positive) scalar multiple of CT, rather than have a matrix full of fractions that can be awkward to read and follow
-
- e.g.
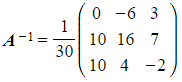
- e.g.
-
Can I use my calculator to get the inverse of a matrix?
- Yes, of course, but only where possible!
- Questions with unknown elements will generally not be solvable directly on a calculator
- If by the end of the questions, the unknowns have been found, you can then check your answers using the calculator
- Some questions with purely numerical matrices may still ask you to show your full working without relying on calculator technology - but you can still use it at the end to check!
- Two things to be very careful with when using your calculator
- When entering values into a matrix, check and be clear as to where the cursor moves to after each element – does it move across or down?
- When displaying a matrix many calculators will display values as (rounded/truncated) decimals; highlighting a particular one will show the value as an exact fraction
Exam Tip
- Do not worry too much about the various terms and language used in finding the inverse of a 3x3 matrix, learning and following the process (without a calculator) is more important
- If a question says not to rely on "calculator technology" in your answer, you must show full working throughout
- However, you can still use your calculator to check your work at the end
- Consider the number of marks a question is worth for a clue as to how much working may be necessary
Worked Example
Given that 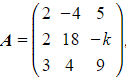 , find
, find ![]() in terms of
in terms of ![]() .
.


转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





