- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Further Maths: Core Pure:复习笔记1.2.2 de Moivre's Theorem
De Moivre's Theorem
What is de Moivre’s Theorem?
- de Moivre’s theorem can be used to find powers of complex numbers
- It states that for
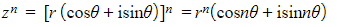
- Where
- z ≠ 0
- r is the modulus, |z|, r ∈ ℝ+
- θ is the argument, arg z, θ ∈ ℝ
- n ∈ ℝ
- Where
- In Euler’s form this is simply:
- In words de Moivre’s theorem tells us to raise the modulus by the power of n and multiply the argument by n
- In the formula booklet de Moivre’s theorem is given in both polar and Euler’s form:
How do I use de Moivre’s Theorem to raise a complex number to a power?
- If a complex number is in Cartesian form you will need to convert it to either modulus-argument (polar) form or exponential (Euler’s) form first
- This allows de Moivre’s theorem to be used on the complex number
- You may need to convert it back to Cartesian form afterwards
- If a complex number is in the form
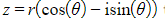 then you will need to rewrite it as
then you will need to rewrite it as 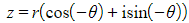 before applying de Moivre’s theorem
before applying de Moivre’s theorem - A useful case of de Moivre’s theorem allows us to easily find the reciprocal of a complex number:
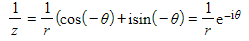
- Using the trig identities cos(-θ) = cos(θ) and sin(-θ) = - sin(θ) gives
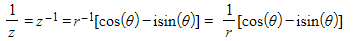
- In general
Exam Tip
- You may be asked to find all the powers of a complex number, this means there will be a repeating pattern
- This can happen if the modulus of the complex number is 1
- Keep an eye on your answers and look for the point at which they begin to repeat themselves
Worked Example
Find the value of  , giving your answer in the form a + bi.
, giving your answer in the form a + bi.

转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





