- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
CIE A Level Maths: Pure 3复习笔记8.3.2 Geometry of Complex Multiplication & Division
Geometry of Complex Multiplication & Division
You now know how conjugation, addition and subtraction affect the geometry of complex numbers on an Argand diagram. Now we can look at the effects of multiplication and division.
What do multiplication and division look like on an Argand diagram?
- Let z1 and z2 be two complex numbers
- With moduli r1 and r2 respectively
- And arguments θ1 and θ2 respectively
- To plot
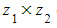 on an Argand diagram
on an Argand diagram
- The modulus will be
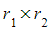
- The argument will be
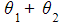
- Subtract 2π from the argument if it is not in the range
- To plot
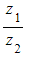 on an Argand diagram
on an Argand diagram
- The modulus will be
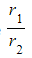
- The argument will be
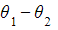
- Add 2π to the argument if it is not in the range
- The modulus will be
- The modulus will be
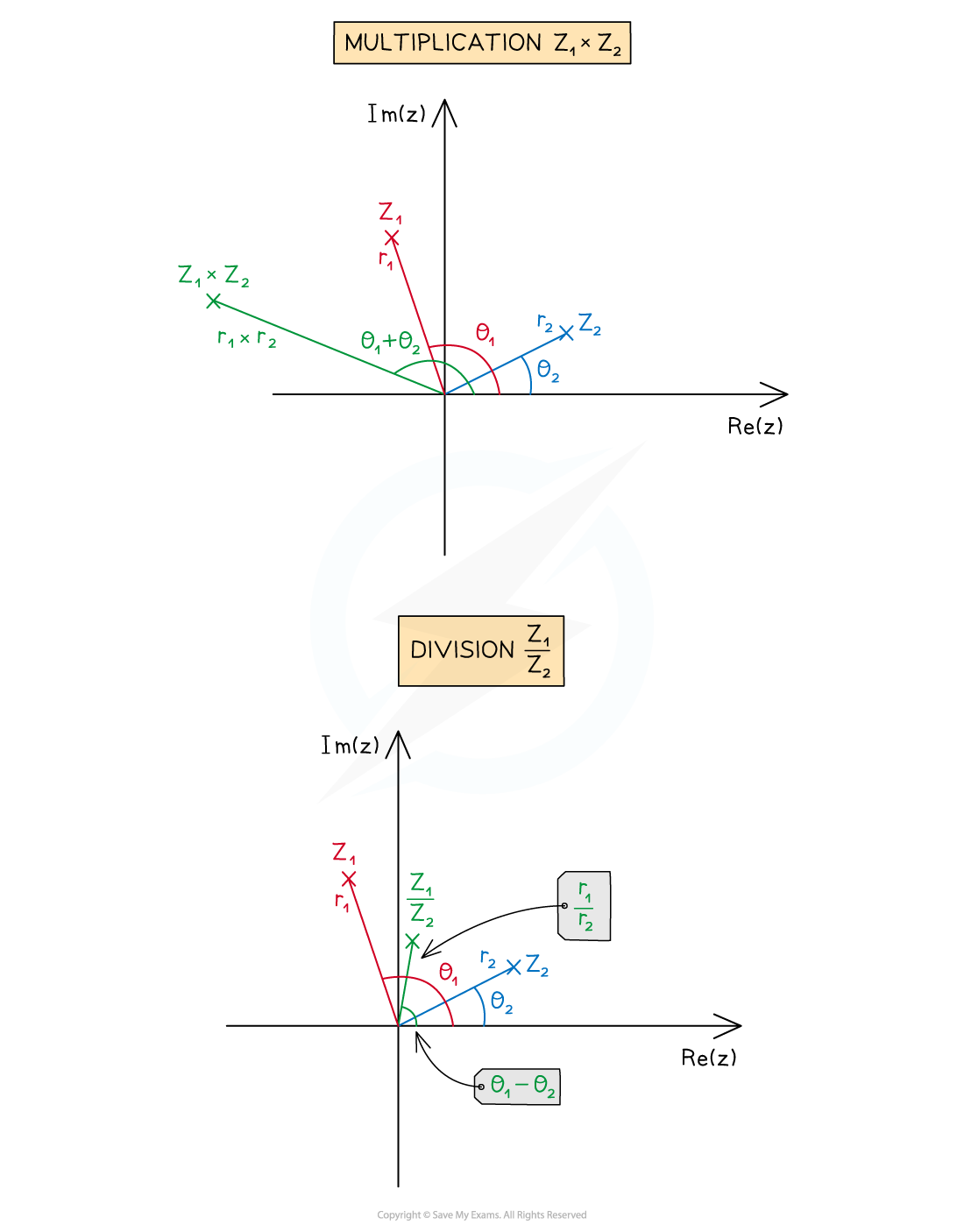
What are the geometric representations of complex multiplication and division?
- Let w be a given complex number with modulus r and argument θ
- In exponential form
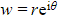
- In exponential form
- Let z be any complex number represented on an Argand diagram
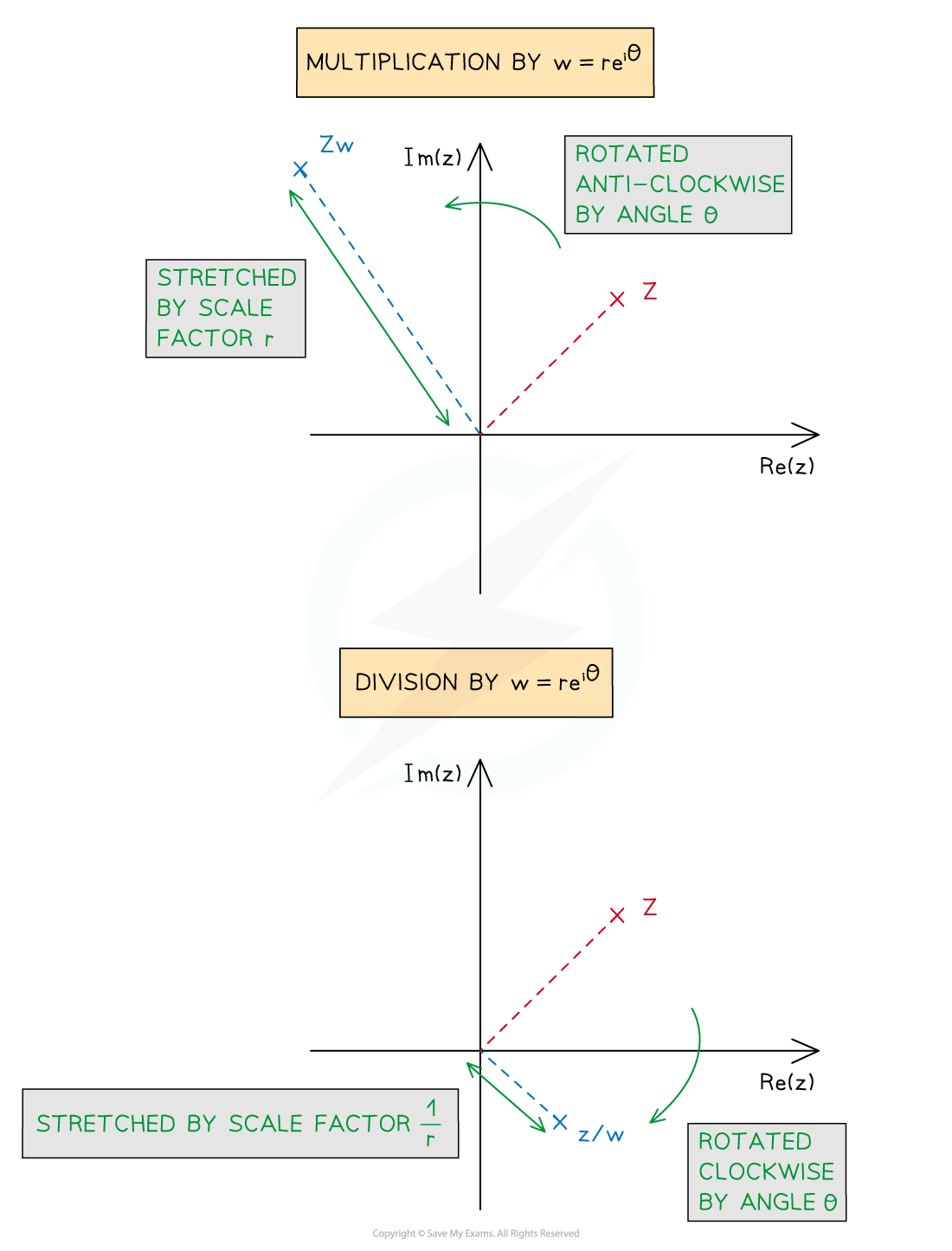
- Multiplying z by w results in z being:
- Stretched from the origin by a scale factor of r
- If r > 1 then z will move further away from the origin
- If 0 < r < 1 then z will move closer to the origin
- If r = 1 then z will remain the same distance from the origin
- Rotated anti-clockwise about the origin by angle θ
- If θ < 0 then the rotation will be clockwise
- Stretched from the origin by a scale factor of r
- Dividing z by w results in z being:
- Stretched from the origin by a scale factor of
- If r > 1 then z will move closer to the origin
- If 0 < r < 1 then z will further away from the origin
- If r = 1 then z will remain the same distance from the origin
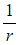
- Rotated clockwise about the origin by angle θ
- If θ < 0 then the rotation will be anti-clockwise
- Stretched from the origin by a scale factor of
Worked Example

Exam Tip
- If a complex number is given in Cartesian form, first convert it to polar form or exponential form to find the modulus and argument.
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





