- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
CIE A Level Maths: Pure 3复习笔记8.3.1 Exponential Form of Complex Numbers
Exponential Form of Complex Numbers
You now know how to do lots of operations with complex numbers: add, subtract, multiply, divide, raise to a power and even square root. The last operation to learn is raising the number e to the power of an imaginary number.
How do we calculate e to the power of an imaginary number?
- Given an imaginary number (iθ) we can define exponentiation as
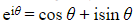
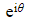 is the complex number with modulus 1 and argument θ
is the complex number with modulus 1 and argument θ
- This works with our current rules of exponents
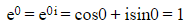
- This shows e to the power 0 would still give the answer of 1
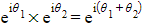
- This is because when you multiply complex numbers you can add the arguments
- This shows that when you multiply two powers you can still add the indices
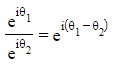
- This is because when you divide complex numbers you can subtract the arguments
- This shows that when you divide two powers you can still subtract the indices
What is the exponential form of a complex number?
- Any complex number
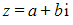 can be written in polar form
can be written in polar form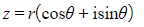
- r is the modulus
- θ is the argument
- Using the definition of
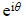 we can now also write Z in exponential form
we can now also write Z in exponential form
Why do I need to use the exponential form of a complex number?
- It's just a shorter and quicker way of expressing complex numbers
- It makes a link between the exponential function and trigonometric functions
- It makes it easier to remember what happens with the moduli and arguments when multiplying and dividing
- If
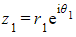 and
and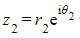 then
then
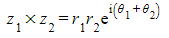
- You can clearly see that the moduli have been multiplied and the arguments have been added

- You can clearly see that the moduli have been divided and the arguments have been subtracted
What are some common numbers in exponential form?
- As
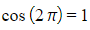 and
and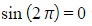 you can write:
you can write:
- Using the same idea you can write:
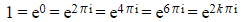 where k is any integer
where k is any integer
- As
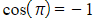 and
and you can write:
you can write:
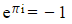
- Or more commonly written as
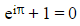
- As
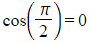 and
and 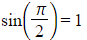 you can write:
you can write:
Worked Example

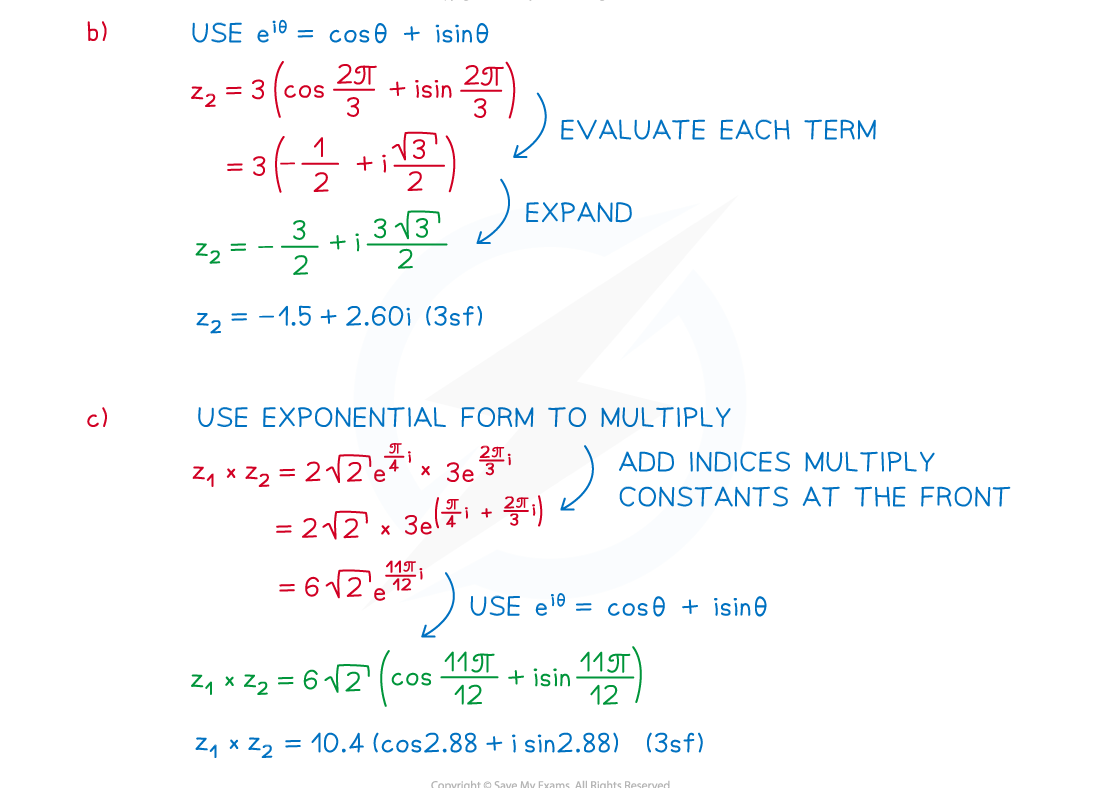
Exam Tip
- The powers can be long and contain fractions so make sure you write the expression clearly.
- You don’t want to lose marks because the examiner can’t read your answer
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





