- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
CIE A Level Maths: Pure 3复习笔记8.1.3 Square Roots of a Complex Number
Square Roots of a Complex Number
How do I find the square root of a complex number?
- The square roots of a complex number will themselves be complex:
- i.e. if
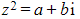 then
then 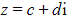
- i.e. if
- We can then square
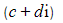 and equate it to the original complex number
and equate it to the original complex number 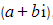 , as they both describe
, as they both describe 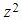 :
:
- Then expand and simplify:
- As both sides are equal we are able to equate real and imaginary parts:
- Equating the real components:
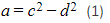
- Equating the imaginary components:
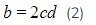
- Equating the real components:
- These equations can then be solved simultaneously to find the real and imaginary components of the square root
- In general, we can rearrange (2) to make
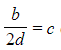 and then substitute into (1)
and then substitute into (1) - This will lead to a quartic equation in terms of d; which can be solved by making a substitution to turn it into a quadratic (see 1.1.5 Further Solving Quadratic Equations (Hidden Quadratics))
- In general, we can rearrange (2) to make
- The values of d can then be used to find the corresponding values of c, so we now have both components of both square roots (
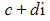 )
) - Note that one root will be the negative of the other root
- g.
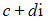 and
and 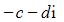
- g.
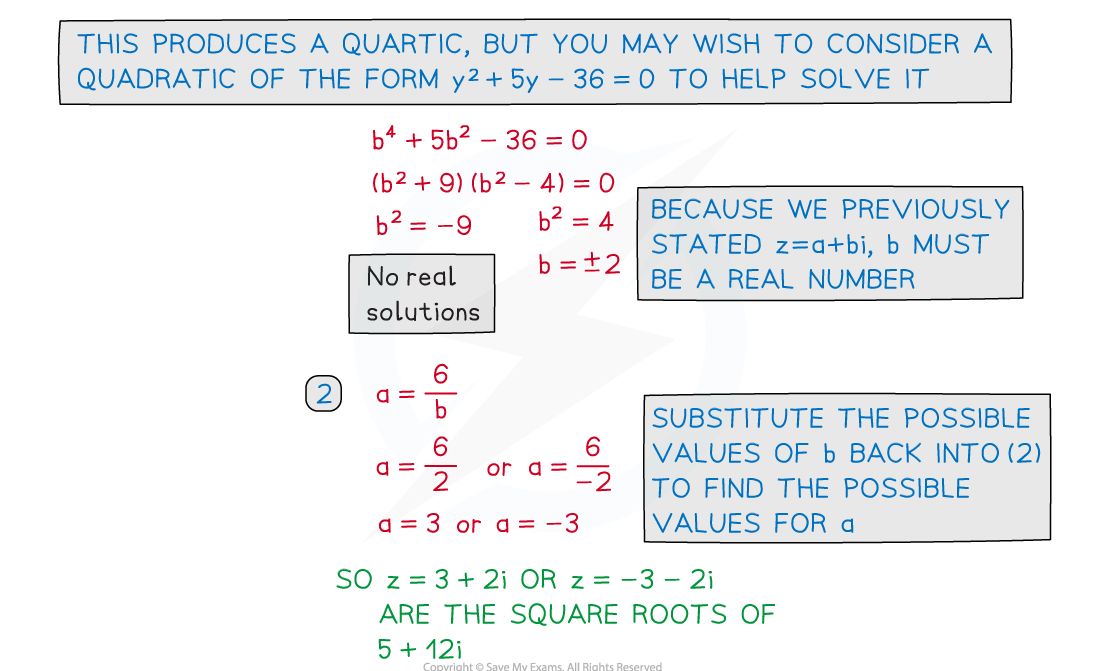
Worked Example

Exam Tip
- Most calculators used at A-Level can handle complex numbers.
- Once you have found the square roots algebraically; use your calculator to square them and make sure you get the number you were originally trying to square-root!
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





