- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
CIE A Level Maths: Pure 3复习笔记7.3.1 Equation of a Line in Vector Form
Equation of a Line in Vector Form
How do I find the vector equation of a line?
- You need to know:
- The position vector of one point on the line
- A direction vector of the line (or the position vector of another point)
- There are two formulas for getting a vector equation of a line:
- r = a + t (b - a)
- use this formula when you know the position vectors a and b of two points on the line
- r = a + t d
- use this formula when you know the position vector a of a point on the line and a direction vector d
- Both forms could be compared to the Cartesian equation of a 2D line
- r = a + t (b - a)
 How do I determine if a point is on a line?
How do I determine if a point is on a line?
- Each different point on the line corresponds to a different value of t
- For example: if an equation for a line is r = 3i + 2j - k + t (i + 2j)
- the point with coordinates (2, 0, -1) is on the line and corresponds to t = -1
- However we know that the point with coordinates (-7, 5, 0) is not on this line
- No value of t could make the k component 0
- For example: if an equation for a line is r = 3i + 2j - k + t (i + 2j)
Can two different equations represent the same line?
- Why do we say a direction vector and not the direction vector? Because the magnitude of the vector doesn’t matter; only the direction is important
- we can multiply any direction vector by a (non-zero) constant and this wouldn’t change the direction
- Therefore there are an infinite number of options for a (a point on the line) and an infinite number of options for the direction vector
- For Cartesian equations – two equations will represent the same line only if they are multiples of each other
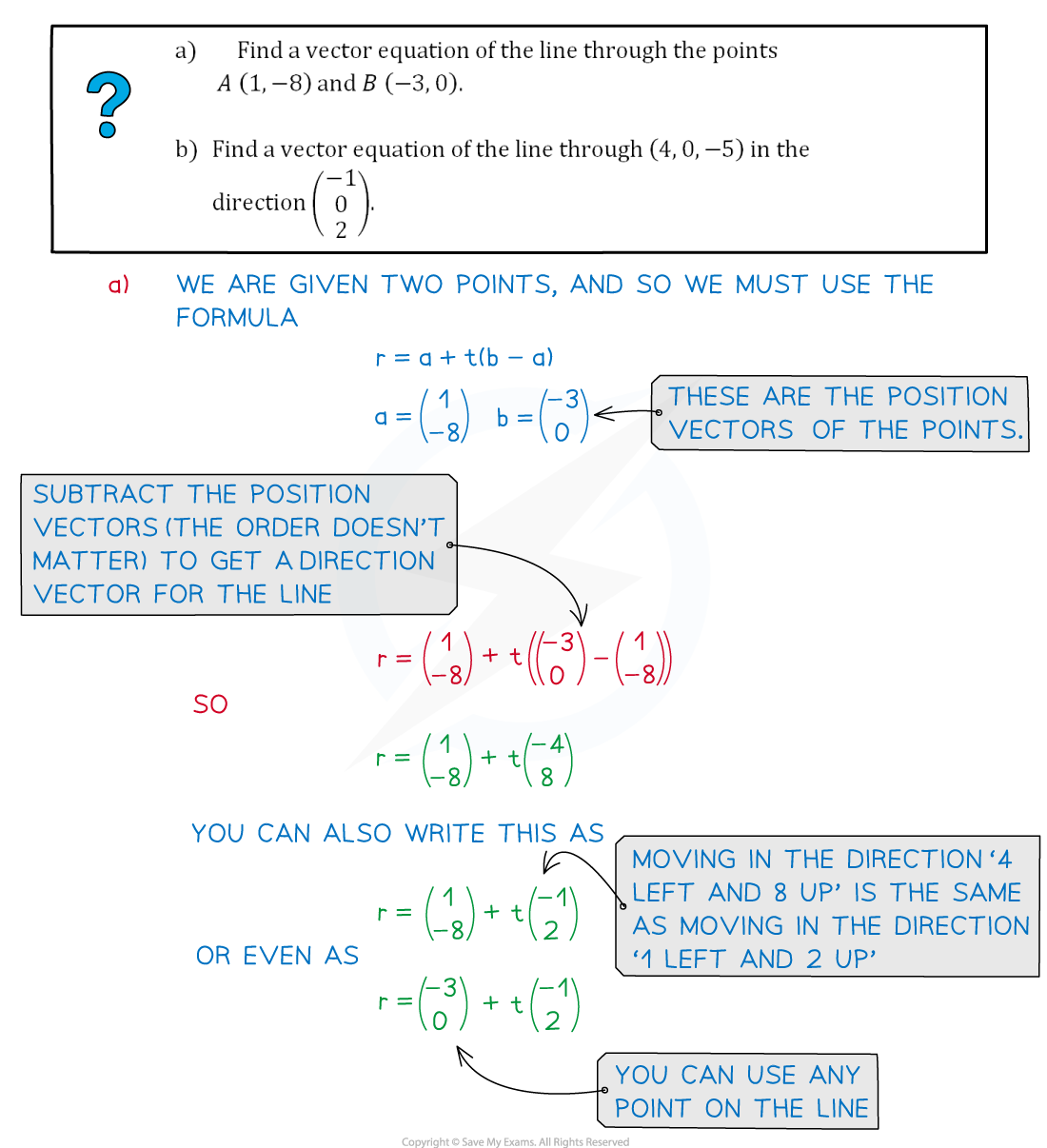
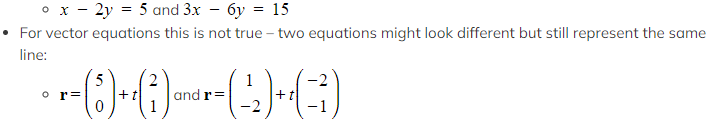 Worked Example
Worked Example

Exam Tip
- Remember that the vector equation of a line can take many different forms. This means that the answer you derive might look different from the answer in a mark scheme.
- You can choose whether to write your vector equations of lines using reference unit vectors or as column vectors – use the form that you prefer!
- If, for example, an exam question uses column vectors, then it is usual to leave the answer in column vectors, but it isn’t essential to do so - you’ll still get the marks!
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





