- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
CIE A Level Maths: Pure 3复习笔记5.1.2 Integrating with Trigonometric Identities
Integrating with Trigonometric Identities
What are trigonometric identities?
- You should be familiar with the trigonometric identities
- Make sure you can find them in the formula booklet
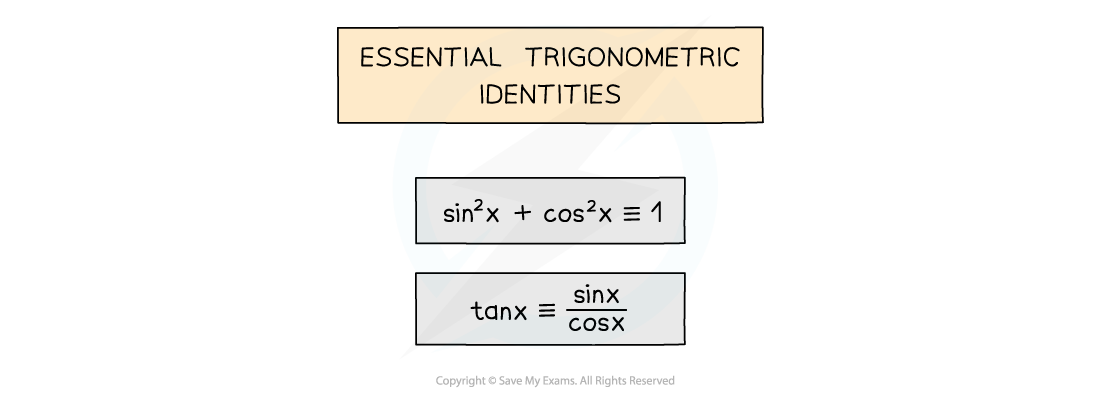
- You may need to use the compound angle formulae or the double angle formulae
- Note the difference between the ± and ∓ symbols!
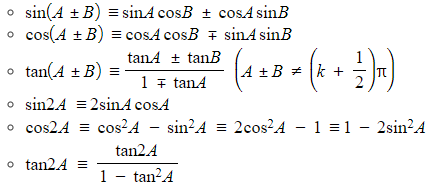
How do I know which trig identities to use?
- There is no set method
- Practice as many questions as possible
- Be familiar with trigonometric functions that can be integrated easily
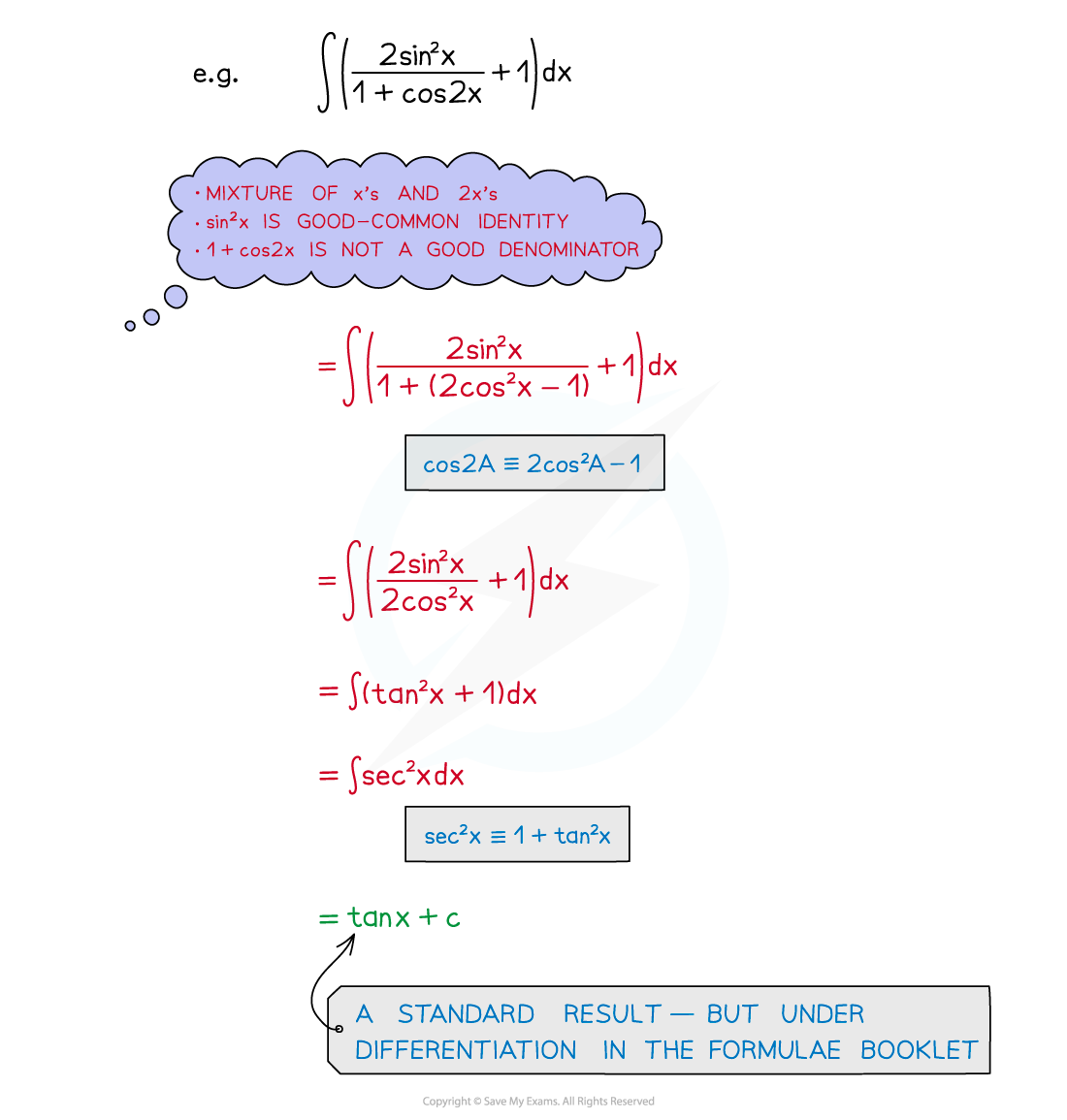
- Be familiar with common identities – especially squared terms
- sin2 x, cos2 x, tan2 x, cosec2 x, sec2 x, tan2 x all appear in identitiesThis is a matter of experience, familiarity and recognition
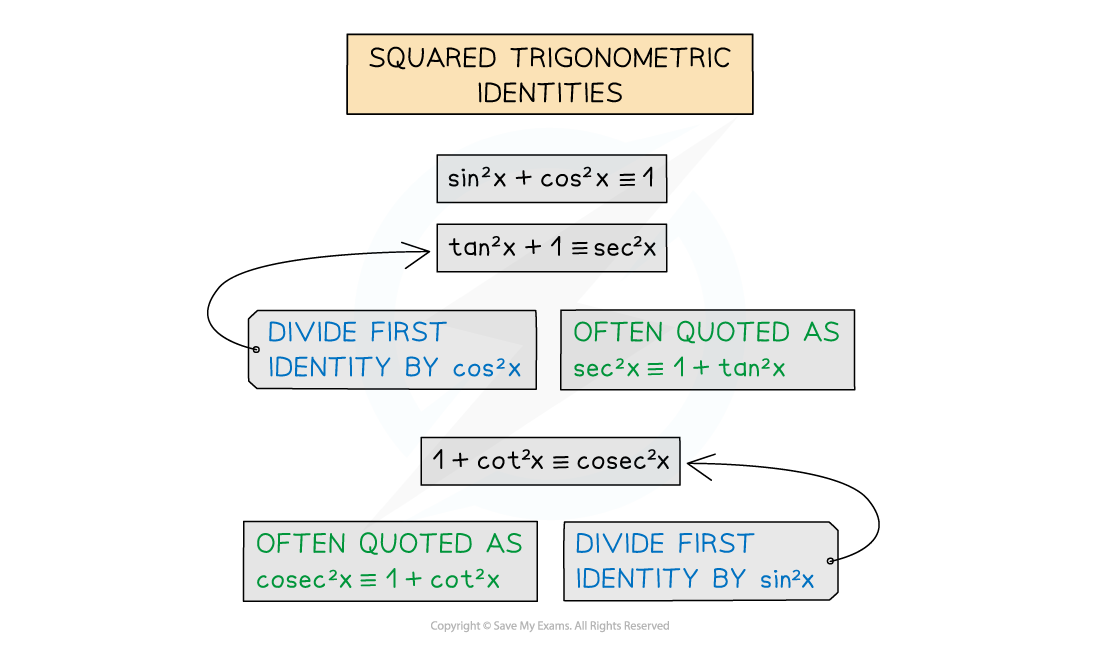
How do I integrate tan2, cot2, sec2 and cosec2?
- The integral of sec2x is tan x (+c)
- This is because the derivative of tan x is sec2x
- The integral of cosec2x is -cot x (+c)
- This is because the derivative of cot x is -cosec2x
- The integral of tan2x can be found by using the identity to rewrite tan2x before integrating:
- 1 + tan2x = sec2x
- The integral of cot2x can be found by using the identity to rewrite cot2x before integrating:
- 1 + cot2x = cosec2x
How do I integrate sin and cos?
- For functions of the form sin kx, cos kx … see Integrating Other Functions
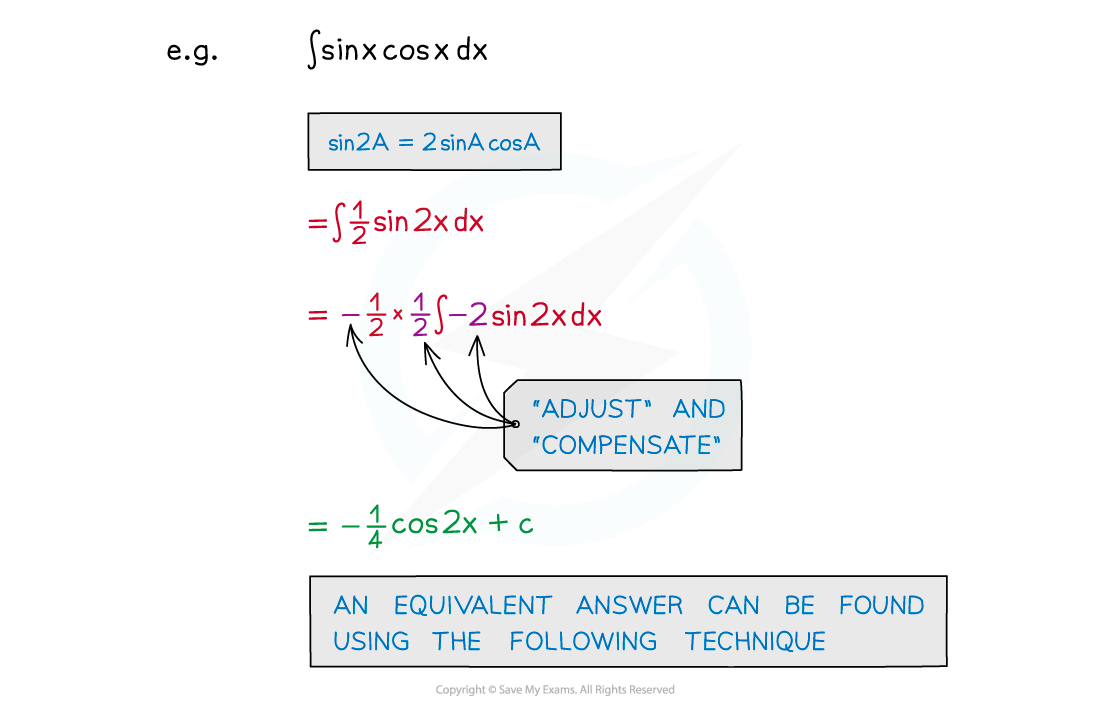
- sin kx × cos kx can be integrated using the identity for sin 2A
- sin 2A = 2sinAcosA
- sinn kx cos kx or sin kx cosn kx can be integrated using reverse chain rule or substitution
- Notice no identity is used here but it looks as though there should be!
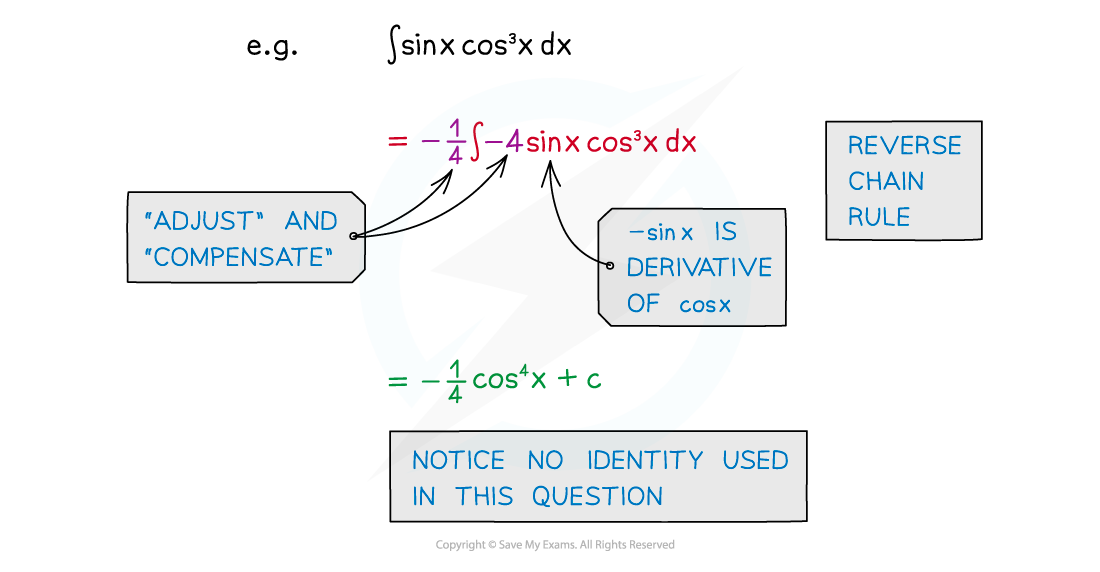
- sin2 kx and cos2 kx can be integrated by using the identity for cos 2A
- For sin2 A, cos 2A = 1 - 2sin2 A
- For cos2 A, cos 2A = 2cos2 A – 1

How do I integrate tan?
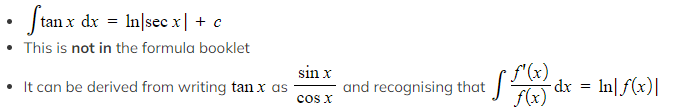 Note that this is in the formula booklet
Note that this is in the formula booklet
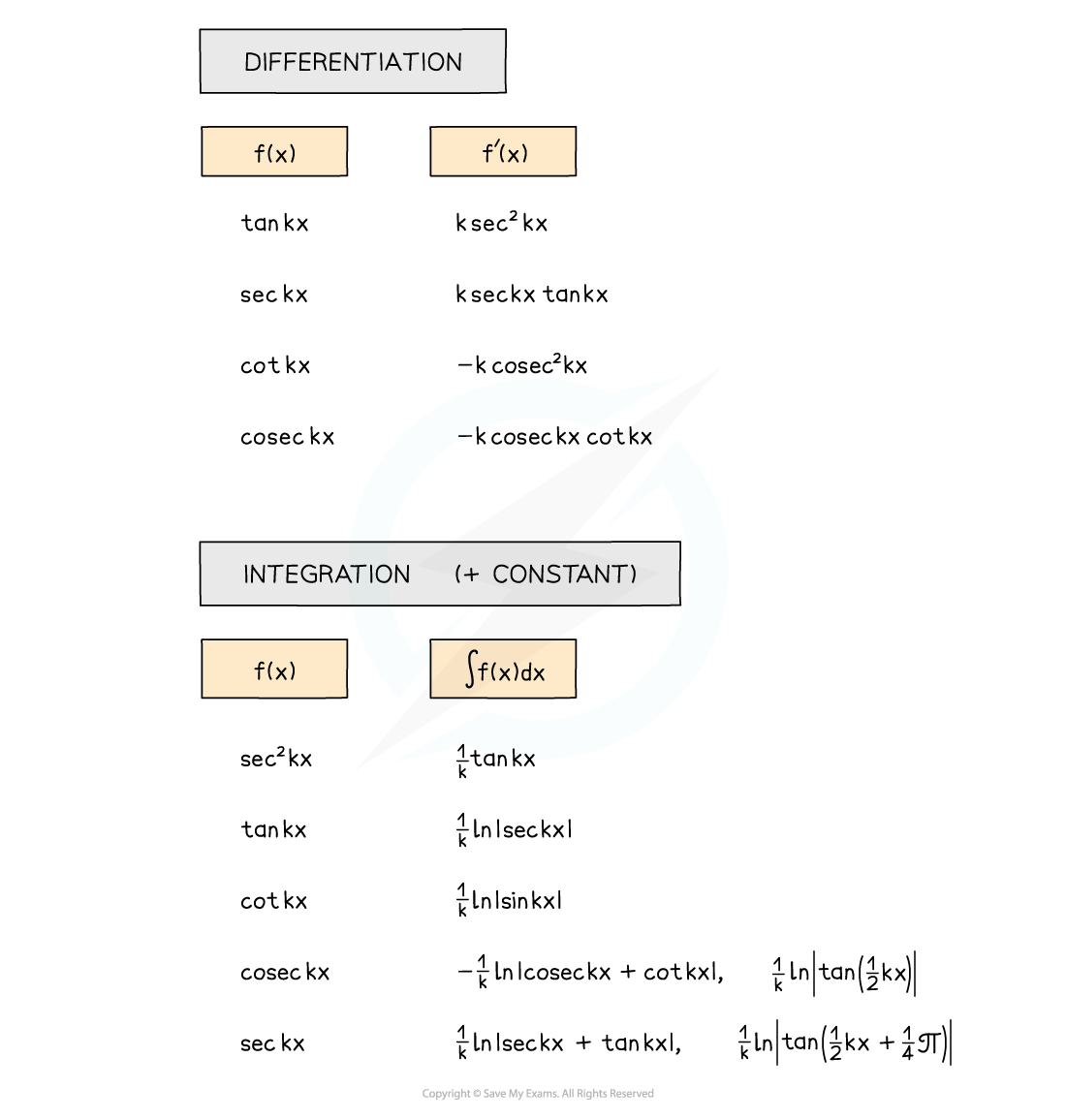
How do I integrate other trig functions?
- The formulae booklet lists many standard trigonometric derivatives and integrals
- Check both the “Differentiation” and “Integration” sections
- For integration using the "Differentiation" formulae, remember that the integral of f'(x) is f(x) !
- Experience, familiarity and recognition are important – practice, practice, practice!
- Problem-solving techniques
Worked Example
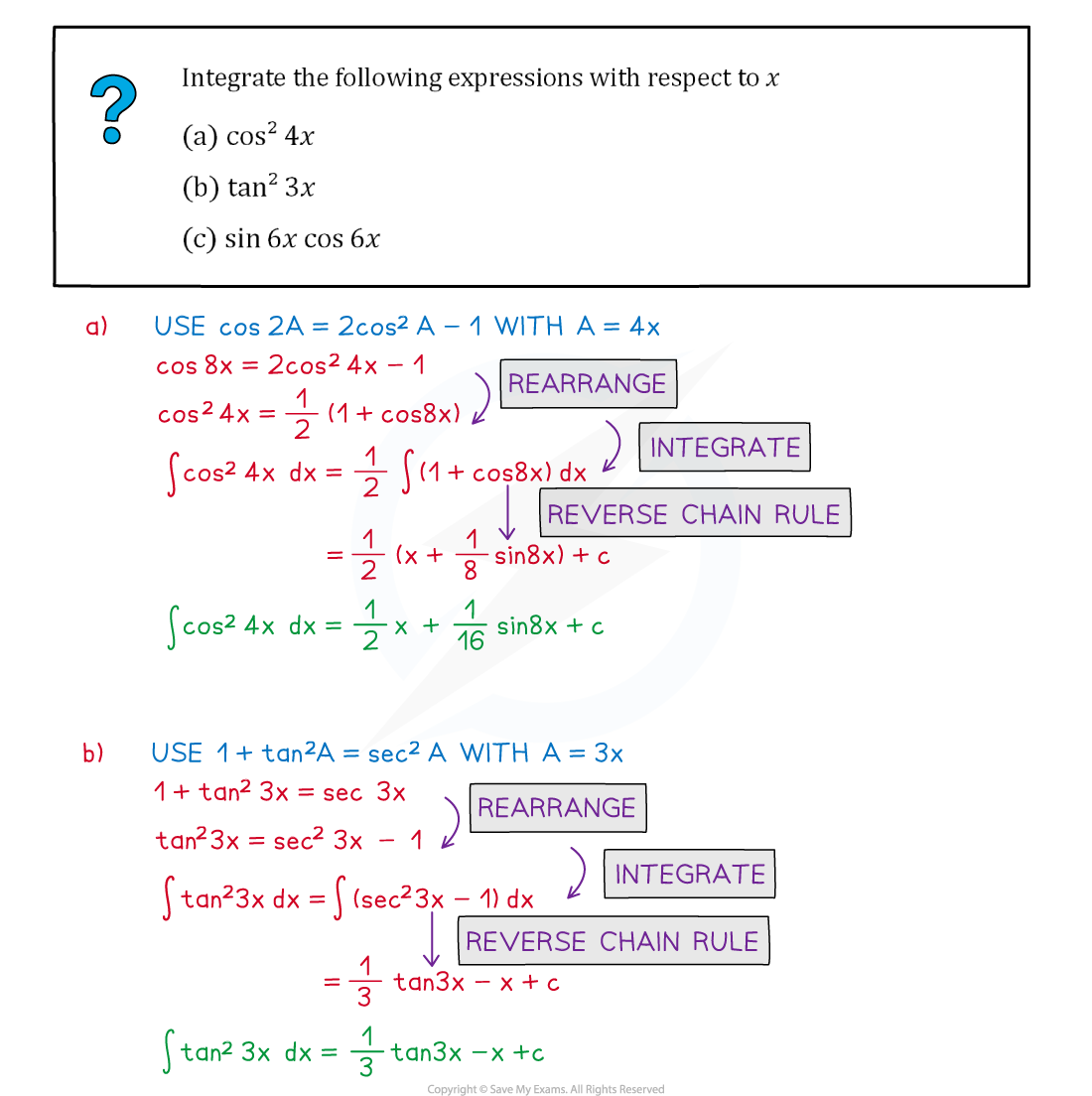
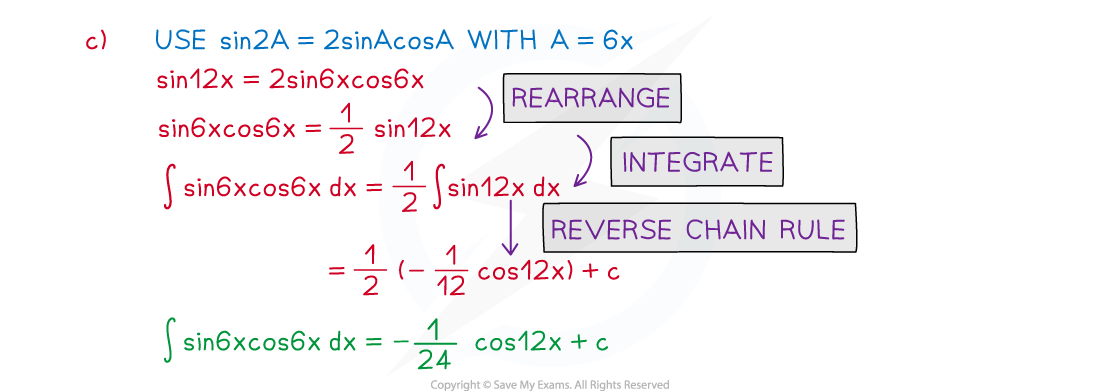
Exam Tip
Make sure you have a copy of the formulae booklet during revision.Questions are likely to be split into (at least) two parts:
-
- The first part may be to show or prove an identity
- The second part may be the integration
If you cannot do the first part, use a given result to attempt the second part.
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





