- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
CIE A Level Maths: Pure 3复习笔记4.3.4 Parametric Differentiation
Parametric Differentiation
How do I find dy/dx from parametric equations?
- Ensure you are familiar with Parametric Equations – Basics first
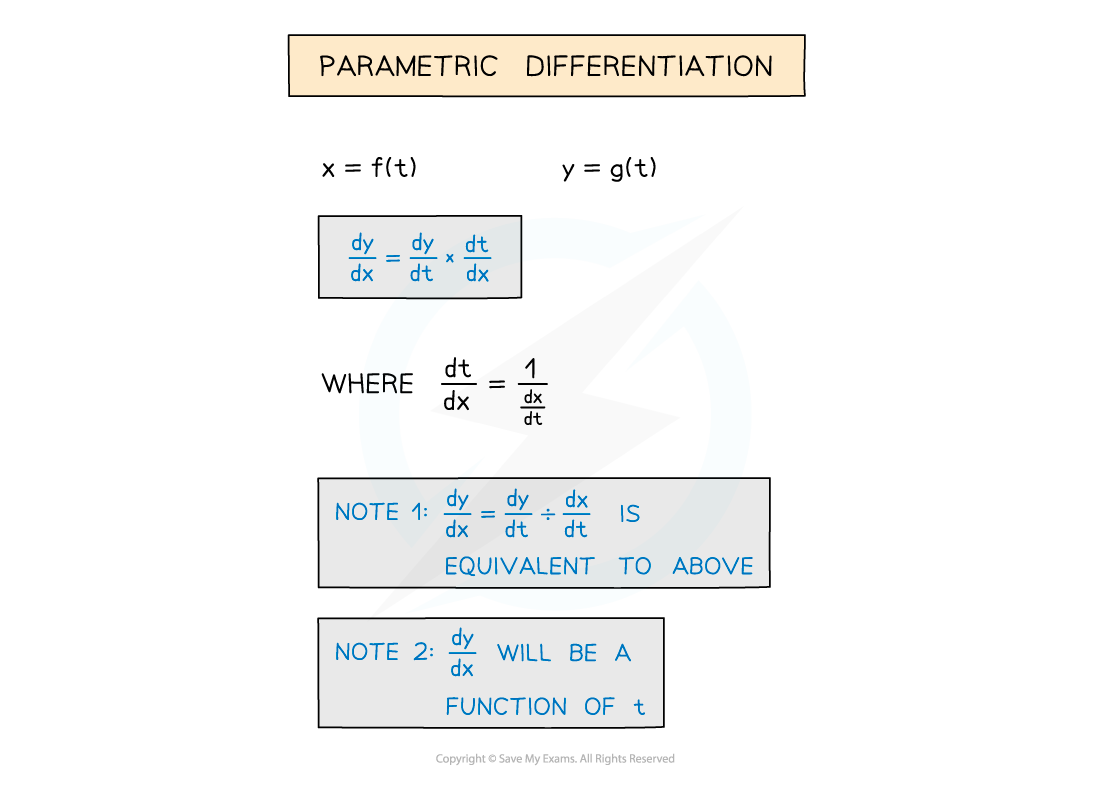
- This method uses the chain rule and the reciprocal property of derivatives
 Questions usually involve finding gradients, tangents and normals
Questions usually involve finding gradients, tangents and normals
- The chain rule is always needed when there are three variables or more – see Connected Rates of Change
How do I find gradients, tangents and normals from parametric equations?
- To find a gradient …
- STEP 1: Find dx/dt and dy/dt
-
- STEP 2: Find dy/dx in terms of t
Using either dy/dx = dy/dt ÷ dx/dt
or dy/dx = dy/dt × dt/dx where dt/dx = 1 ÷ dx/dt
-
- STEP 3: Find the value of t at the required point
- STEP 4: Substitute this value of t into dy/dx to find the gradient
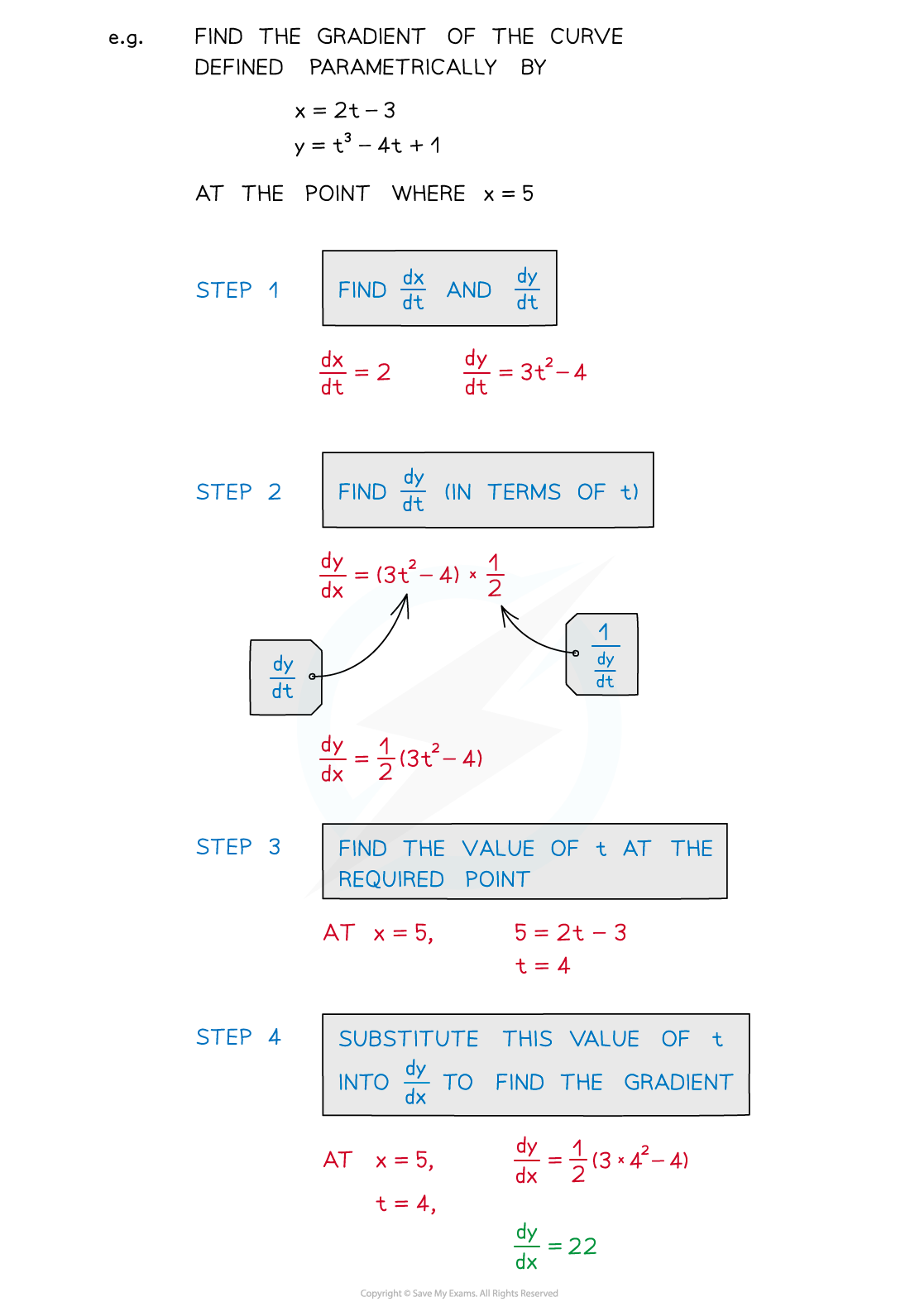
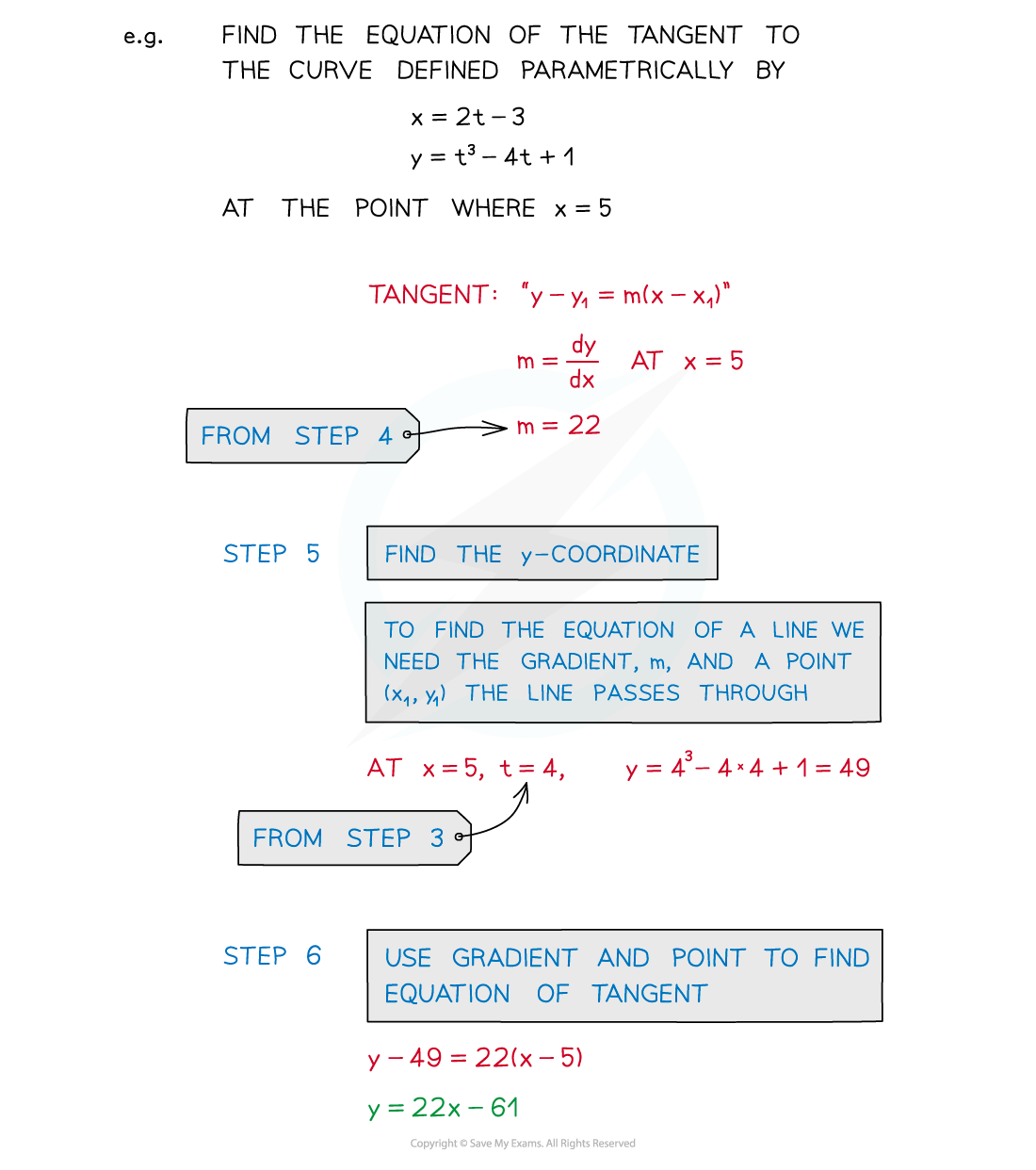
- to then go on to find the equation of a tangent …
- STEP 5: Find the y coordinate
- STEP 6: Use the gradient and point to find the equation of the tangent
- To find a normal...
- STEP 7: Use perpendicular lines property to find the gradient of the normal m1 × m2 = -1
- STEP 8: Use gradient and point to find the equation of the normal y - y1 = m(x - x1)
What else may I be asked to do?
- Questions may require use of tangents and normals as per the coordiante geometry sections
- Find points of intersection between a tangent/normal and x/y axes
- Find areas of basic shapes enclosed by axes and/or tangents/normal
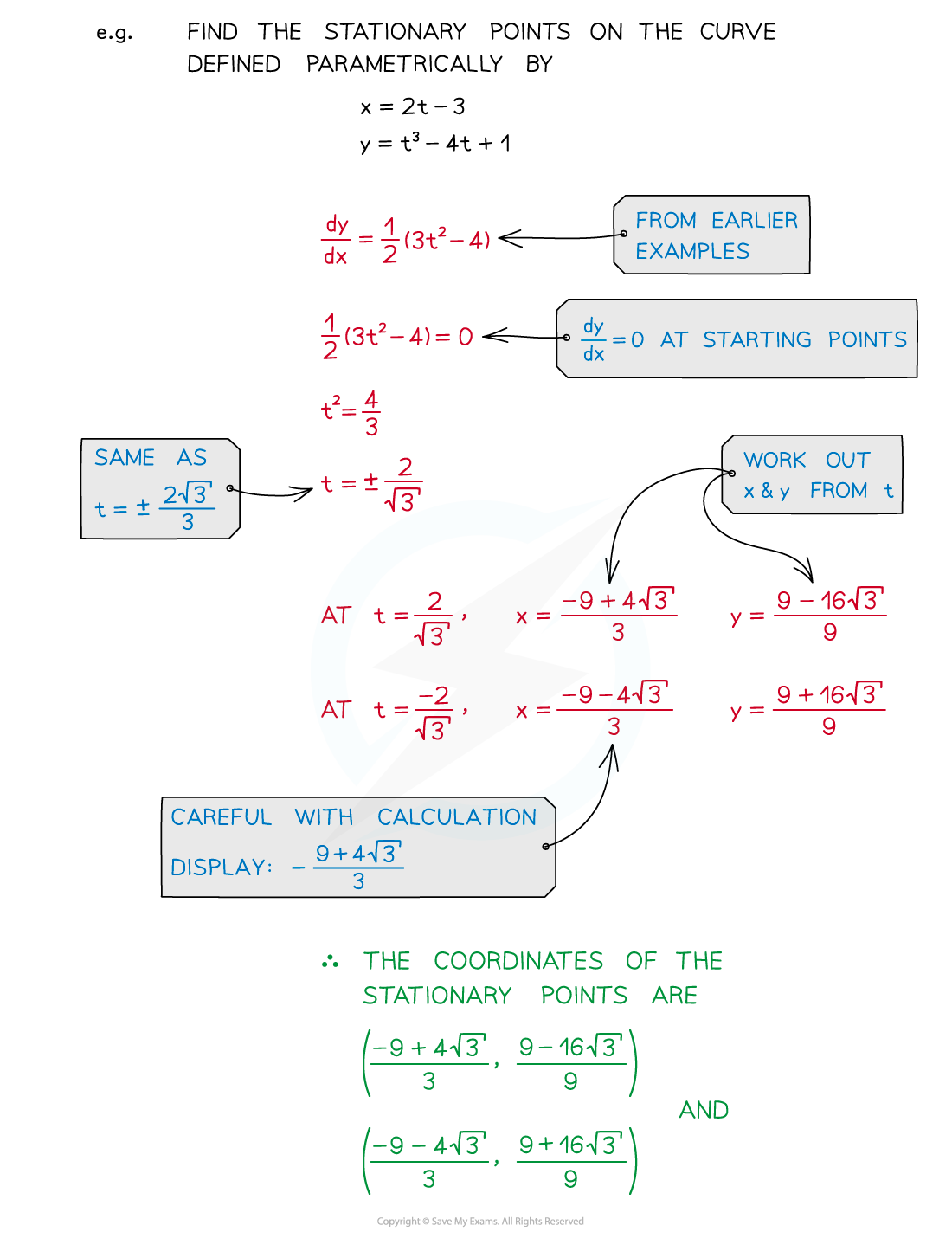
- Find stationary points (dy/dx = 0)
- You may also be asked about horizontal and vertical tangents
- At horizontal (parallel to the x-axis) tangents, dy/dt = 0
- At vertical (parallel to y-axis) tangents, dx/dt = 0
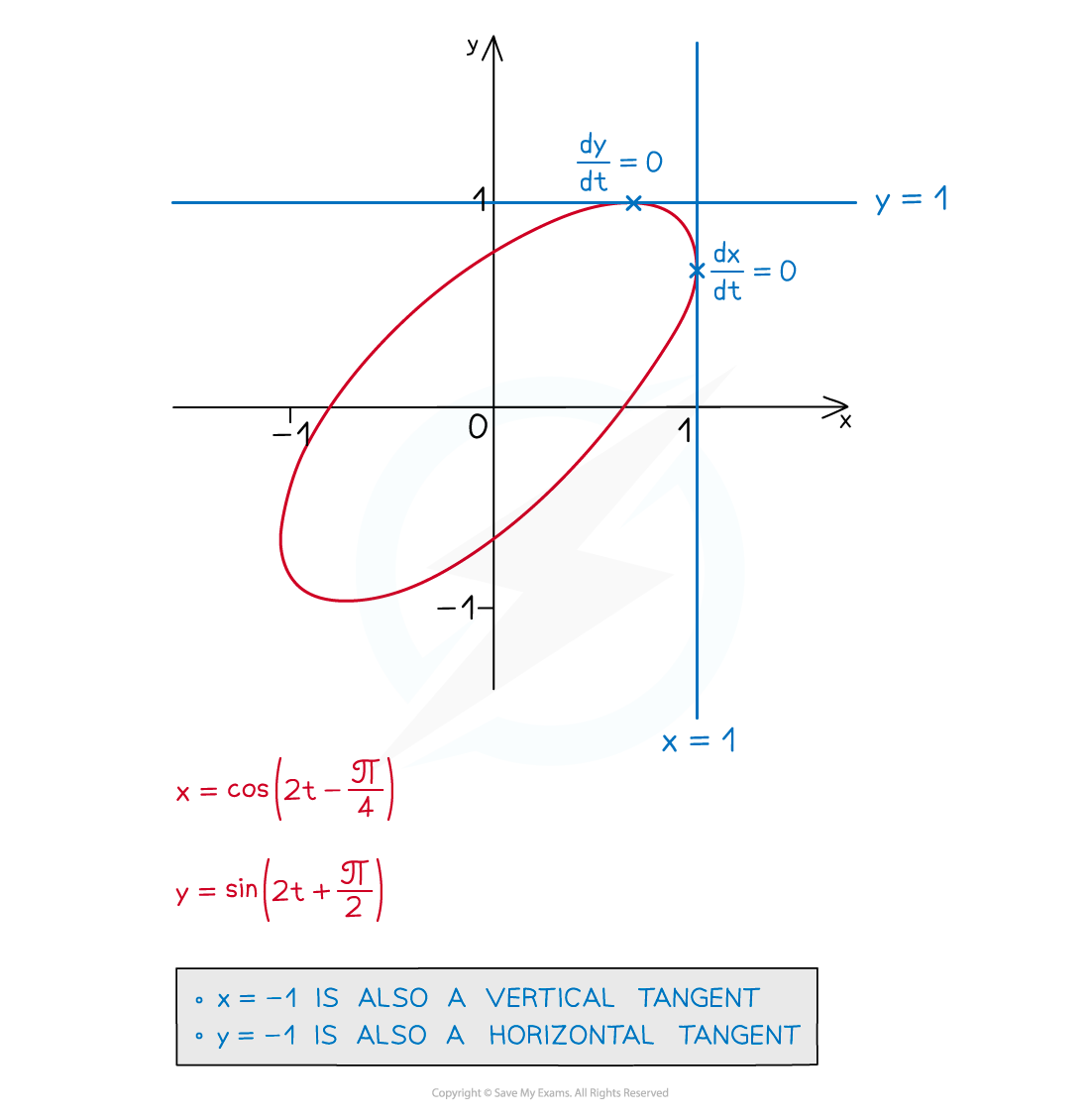
Just for fun …
- Try plotting the graph from the question below using graphing software
- Plenty of free online tools do this – for example Desmos and Geogebra
- Try changing the domain of t to -π/3 ≤ t ≤ π/3
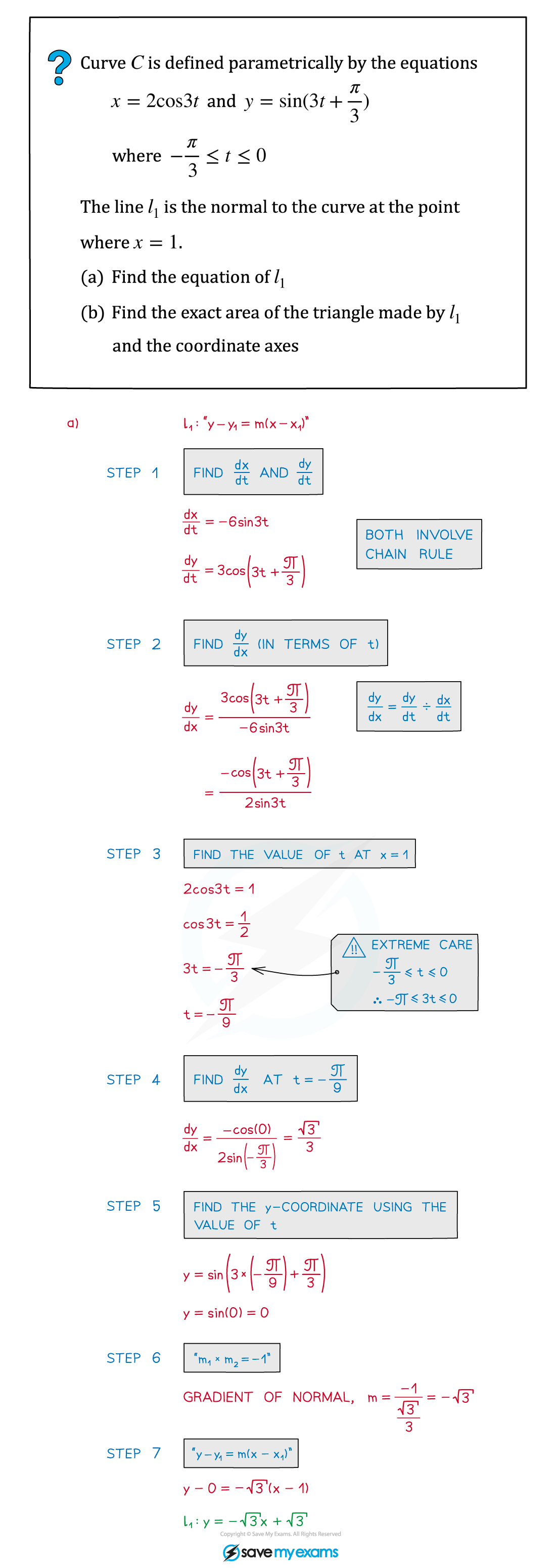
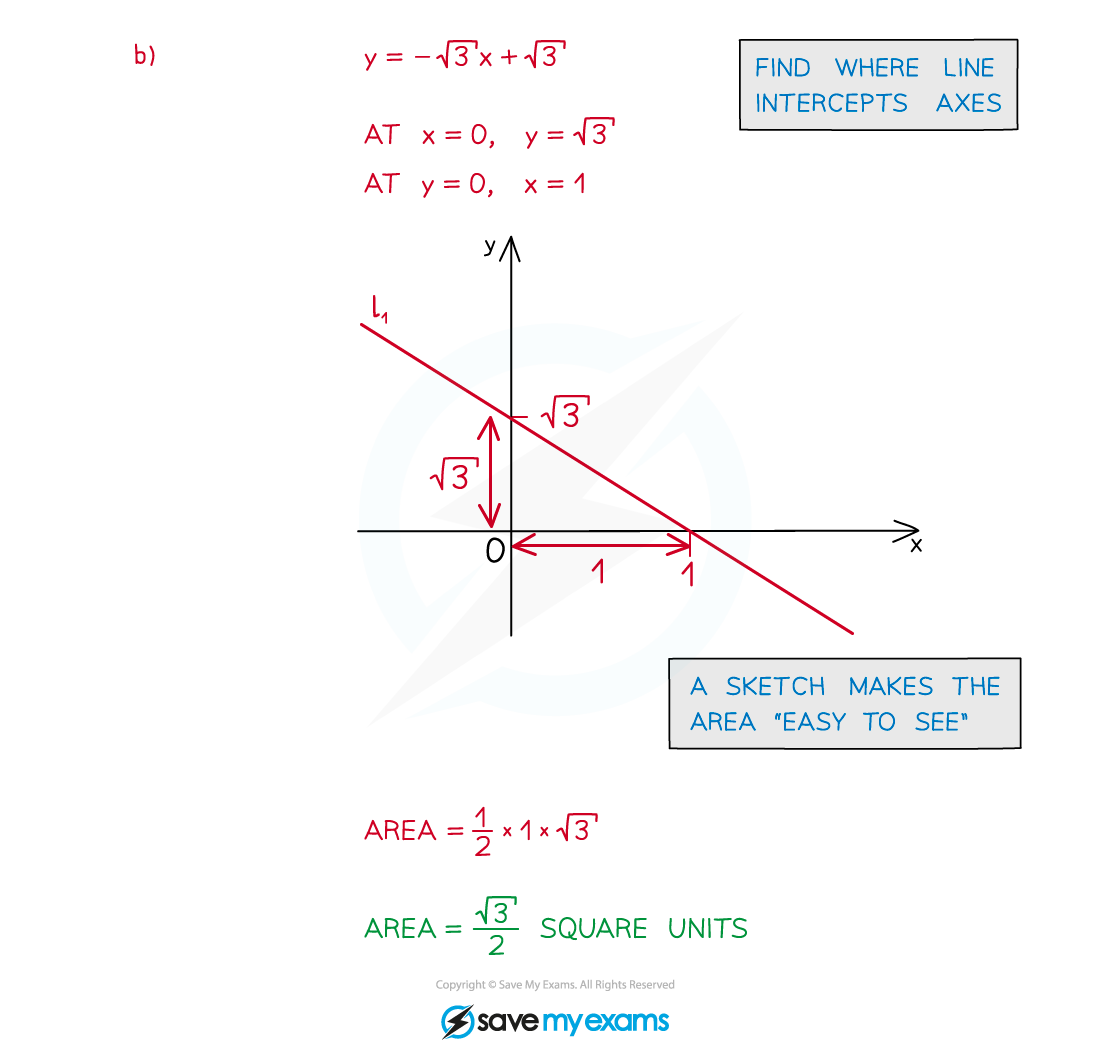
Worked Example
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





