- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
CIE A Level Maths: Mechanics复习笔记4.1.3 Energy Principles
Conservation of Energy
What is conservation of energy?
- The principle of conservation of mechanical energy states that when a particle is moving and no external forces other than gravity act to do work on it, then the total sum of its kinetic energy and the gravitational potential energy will remain constant
- Depending on how the particle is moving, either kinetic energy will be transferred to gravitational potential energy or gravitational potential energy will be transferred to kinetic energy
- If a particle’s height increases it will gain GPE and so must lose KE (and must be slowing down)
- Increase in GPE = Decrease in KE
- If a particle’s speed increases, it will gain KE and so must lose GPE (and must be moving downwards)
- Increase in KE = Decrease in GPE
How is conservation of energy used on an inclined plane?
- If the particle is travelling on an inclined plane it is important to make sure you find the vertical distance before calculating the change in GPE
 It is important to make sure that the only force acting on the particle is gravity before applying the principle of conservation of mechanical energy
It is important to make sure that the only force acting on the particle is gravity before applying the principle of conservation of mechanical energy
- Check that there is no friction by making sure that the plane is a smooth plane
- The normal reaction force, R, will be acting perpendicular to the plane and so will do no work on the particle
- Conservation of energy is often used on a particle that has been projected up a smooth slope with no other external forces acting on it, as it moves up the slope it gains GPE but loses KE
How is conservation of energy used with projectiles?
- Sometimes problems involving projectiles can be solved using energy principles
- There are no external forces acting on the particle other than gravity
- The total energy will not change whilst the particle is in motion
- Energy principles are useful to use instead of 'suvat' if mass is known or needed
Worked Example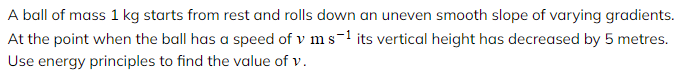
Exam Tip
- Look out for terms such as held at rest or comes to rest, meaning that the start or finish speed is zero. Check that units are in metres, seconds and kilograms before carrying out any question.
Work-Energy Principle
What is the work - energy principle?
- If one or more external forces other than gravity act on a particle during its motion then its total energy can change
- The work - energy principle states that the 'the net work done by external forces = the total change in kinetic energy'
- In problems with more than one force acting on the particle, the net work done by all external forces, including gravity will be equal to the change in kinetic energy only
- Rearranging this such that the work done by gravity is on the other side of the equation gives the result 'work done by all forces except weight is equal to the change in mechanical energy'
- If a particle has to overcome a resistive force such as friction it will lose kinetic energy
- The work - energy principle is particularly useful in problems when we do not know that motion is in a straight line
- As long as we know the change in vertical height between the start and finish the work – energy principle can be applied
- The particle does not need to have taken a direct route to get from the start to the finish point
- The work - energy principle can also be used in problems where acceleration is not constant
- This makes it particularly useful as it can sometimes be used when is not possible
- If it is not known that acceleration is constant then you should use energy methods to solve the problem rather than the 'suvat' equations
How is the work – energy principle used on an inclined plane?
- If the particle is travelling on an inclined plane it is important to make sure you find the vertical distance before calculating the change in GPE
- If the surface is defined as a rough surface then the particle will have to overcome friction and so will have to do work
- This is a hint that it is a problem involving the work – energy principle
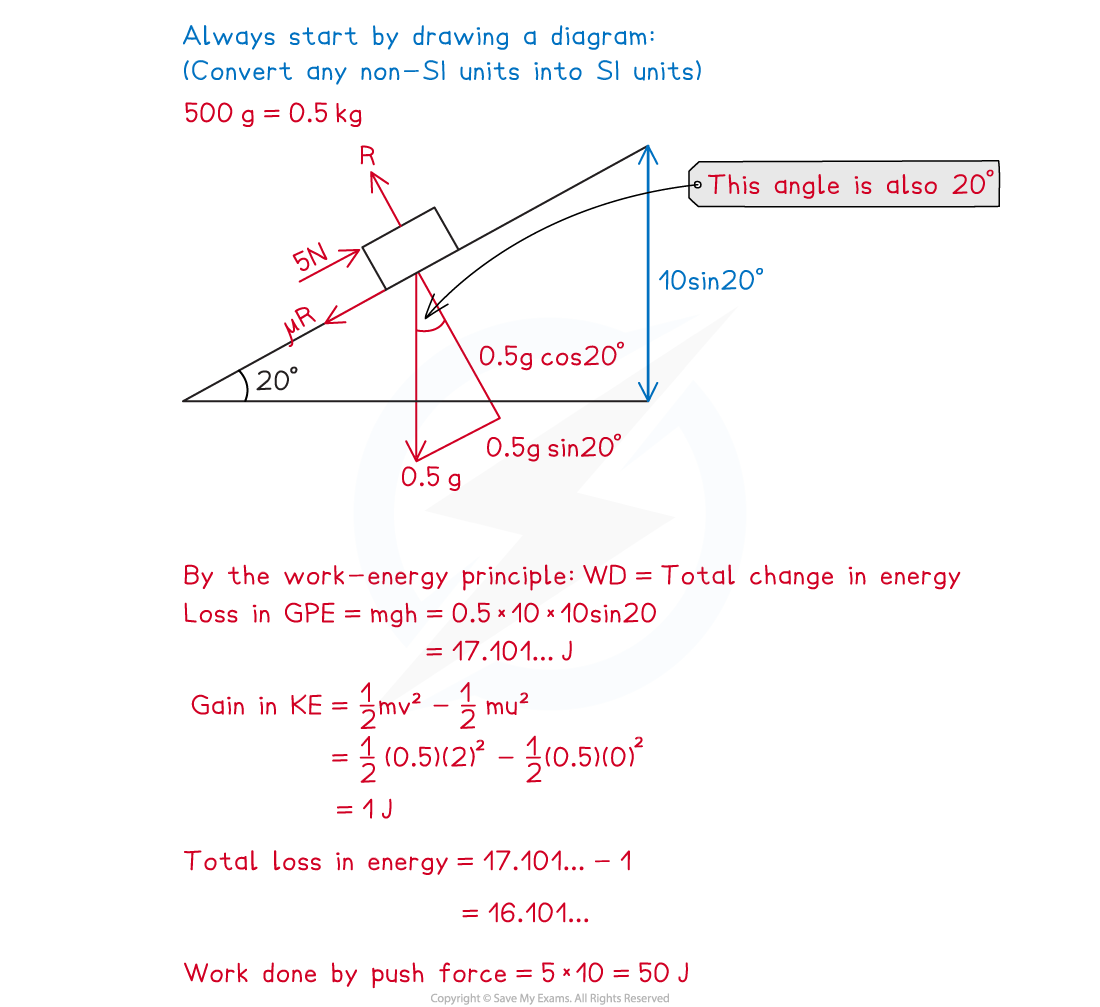
Worked Example
A dog uses a constant force of 5 N to push its toy of mass 500 grams up a rough slope inclined at 20° to the horizontal. The toy starts from rest and after moving 10 metres up the line of greatest slope it is travelling at 1 m s-1. Given that the force is acting parallel to the slope, find the coefficient of friction between the toy and the slope.

Exam Tip
- Look out for questions that don’t explicitly say that motion is linear or acceleration is constant, these are hints that you should use the principle of conservation of mechanical energy instead of the 'suvat' equations. If you’re unsure try to use the energy methods first to solve a problem.
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





