- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
CIE A Level Physics复习笔记22.3.3 Calculating Discrete Energies
Calculating Discrete Energies
- The difference between two energy levels is equal to a specific photon energy
- The energy (hf) of the photon is given by:
ΔE = hf = E2 - E1
- Where,
- E1 = Energy of the higher level (J)
- E2 = Energy of the lower level (J)
- h = Planck’s constant (J s)
- f = Frequency of photon (Hz)
- Using the wave equation, the wavelength of the emitted, or absorbed, radiation can be related to the energy difference by the equation:
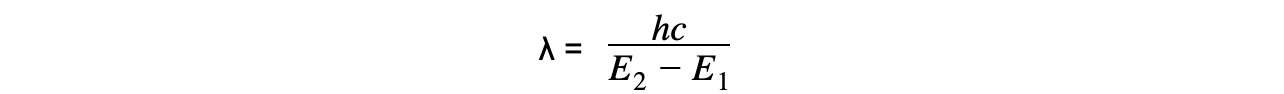
- This equation shows that the larger the difference in energy of two levels ΔE , the shorter the wavelength λ and vice versa
Worked Example
Some electron energy levels in atomic hydrogen are shown below.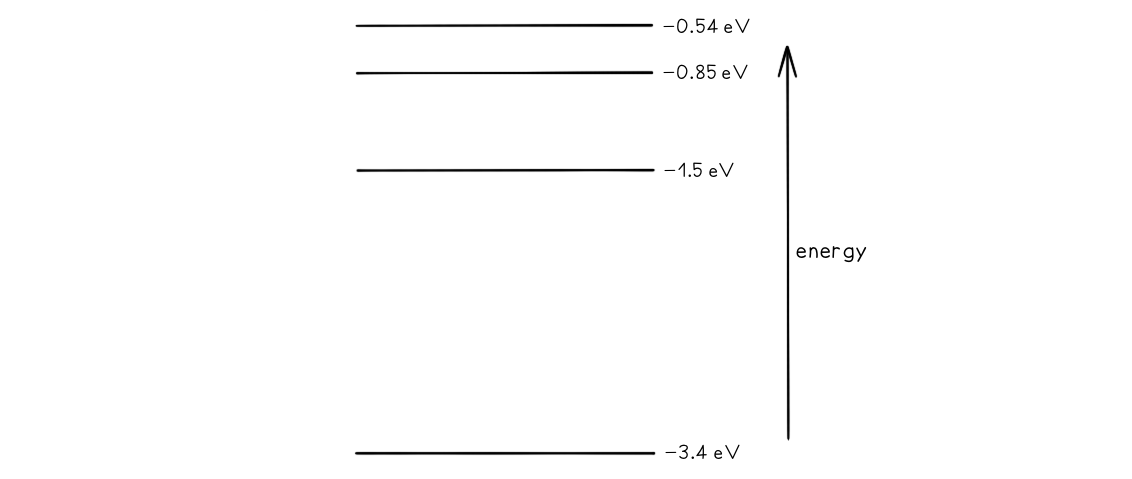
The longest wavelength produced as a result of electron transitions between two of the energy levels is 4.0 × 10–6 m.a) Draw and mark:
- The transition giving rise to the wavelength of 4.0 × 10–6 m with letter L.
- The transition giving rise to the shortest wavelength with letter S.
b) Calculate the wavelength for the transition giving rise to the shortest wavelength.
Part (a)
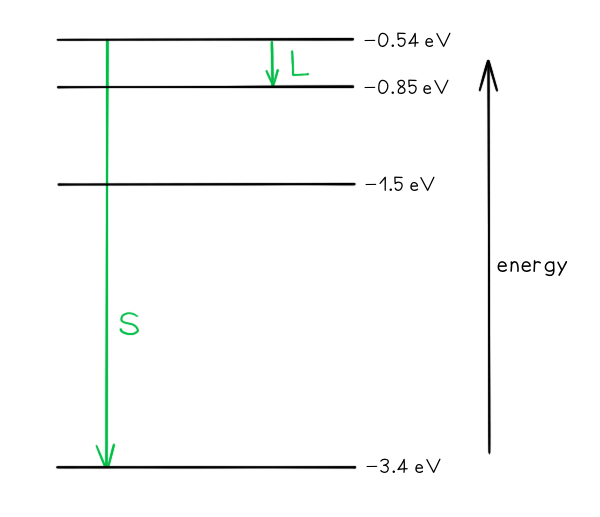
Photon energy and wavelength are inversely proportional, so the largest energy change corresponds to the shortest wavelength (line S) and the smallest energy change corresponds to the longest wavelength (line L)
Part (b)
Step 1: Write down the equation linking the wavelength and the energy levels
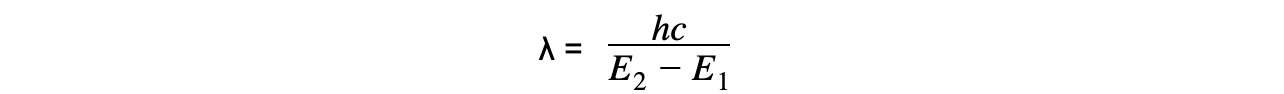
Step 2: Identify the energy levels giving rise to the shortest wavelength
E1 = 0.54 eV
E2 = 3.4 eV
Step 3: Calculate the wavelength
To convert from eV → J: multiply by 1.6 × 10-19
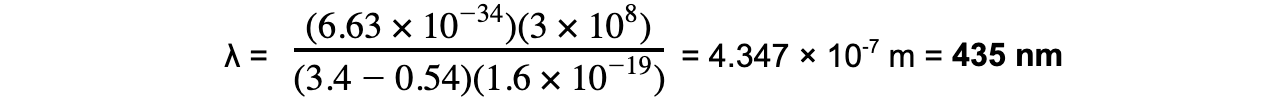
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





