- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
CIE A Level Physics复习笔记20.1.6 Hall Voltage
Hall Voltage
- The Hall voltage is a product of the Hall effect
- Hall voltage is defined as:
The potential difference produced across an electrical conductor when an external magnetic field is applied perpendicular to the current through the conductor
- When an external magnetic field is applied perpendicular to the direction of current through a conductor, the electrons experience a magnetic force
- This makes them drift to one side of the conductor, where they all gather and becomes more negatively charged
- This leaves the opposite side deficient of electrons, or positively charged
- There is now a potential difference across the conductor
- This is called the Hall Voltage, VH

The positive and negative charges drift to opposite ends of the conductor producing a hall voltage when a magnetic field is applied
- An equation for the Hall voltage VH is derived from the electric and magnetic forces on the charges
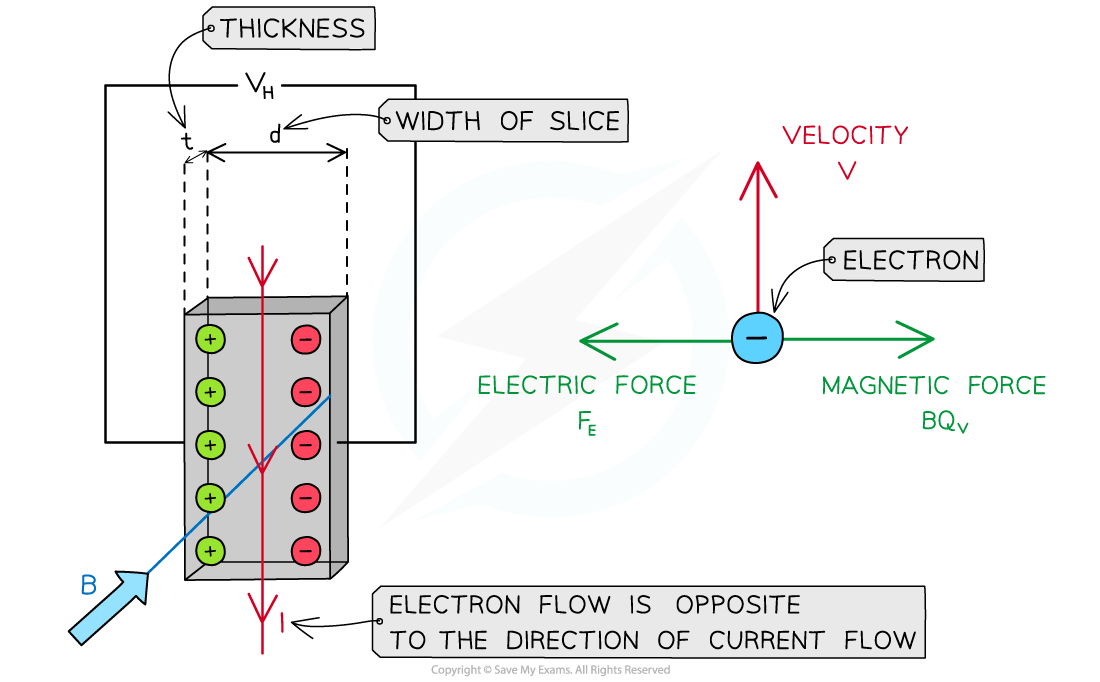
The electric and magnetic forces on the electrons are equal and opposite
- The voltage arises from the electrons accumulating on one side of the conductor slice
- As a result, an electric field is set up between the two opposite sides
- The two sides can be treated like oppositely charged parallel plates, where the electric field strength E is equal to:
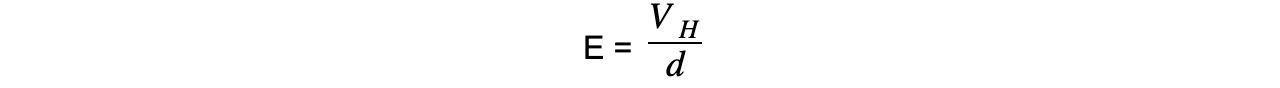
- Where:
- VH = Hall voltage (V)
- d = width of the conductor slice (m)
- A single electron has a drift velocity of v within the conductor. The magnetic field is into the plane of the page, therefore the electron has a magnetic force FB to the right:
FB = Bqv
- This is equal to the electric force FE to the left:
FE = qE
qE = Bqv
- Substituting E and cancelling the charge q
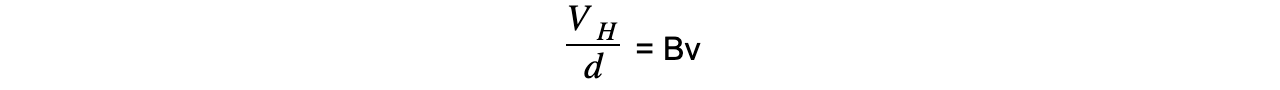
- Recall that current I is related to the drift velocity v by the equation:
I = nAvq
- Where:
- A = cross-sectional area of the conductor (m2)
- n = number density of electrons (m-3)
- Rearranging this for v and substituting it into the equation gives:
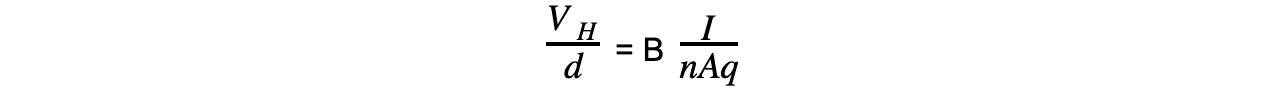
- The cross-sectional area A of the slice is the product of the width d and thickness t:
A = dt
- Substituting A and rearranging for the Hall voltage VH leads to the equation:
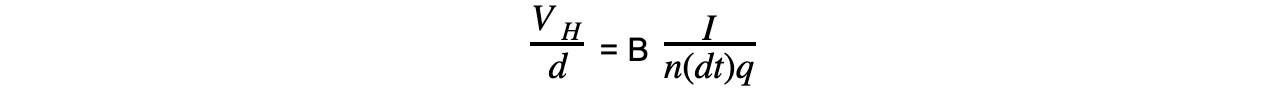
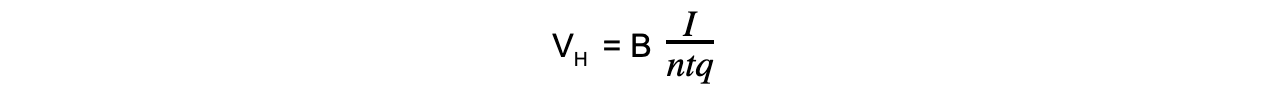
- Where:
- B = magnetic flux density (T)
- q = charge of the electron (C)
- I = current (A)
- n = number density of electrons (m-3)
- t = thickness of the conductor (m)
- This equation shows that the smaller the electron density n of a material, the larger the magnitude of the Hall voltage
- This is why a semiconducting material is often used for a Hall probe
- Note: if the electrons were placed by positive charge carriers, the negative and positive charges would still deflect in opposite directions
- This means there would be no change in the polarity (direction) of the Hall voltage
Exam Tip
Remember to use Fleming’s left-hand rule to obtain the direction the electrons move due to the magnetic force created by the magnetic field.
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





