- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
AQA A Level Maths: Statistics复习笔记4.4.1 Modelling with Distributions
Modelling with Distributions
When should I use a binomial distribution?
- A random variable that follows a binomial distribution is a discrete random variable
- A binomial distribution is used when the random variable counts something
- The number of successful trials
- The number of members of a sample that satisfy a criterion (satisfying the criteria can be seen as a successful trial)
- There are four conditions that X must fulfil to follow a binomial distribution
- There is a fixed finite number of trials (n)
- The trials are independent
- There are exactly two outcomes of each trial (success or failure)
- The probability of success (p) is constant
When should I use a normal distribution?
- A random variable that follows a normal distribution is a continuous random variable
- A normal distribution is used when the random variable measures something and the distribution is:
- Symmetrical
- Bell-shaped
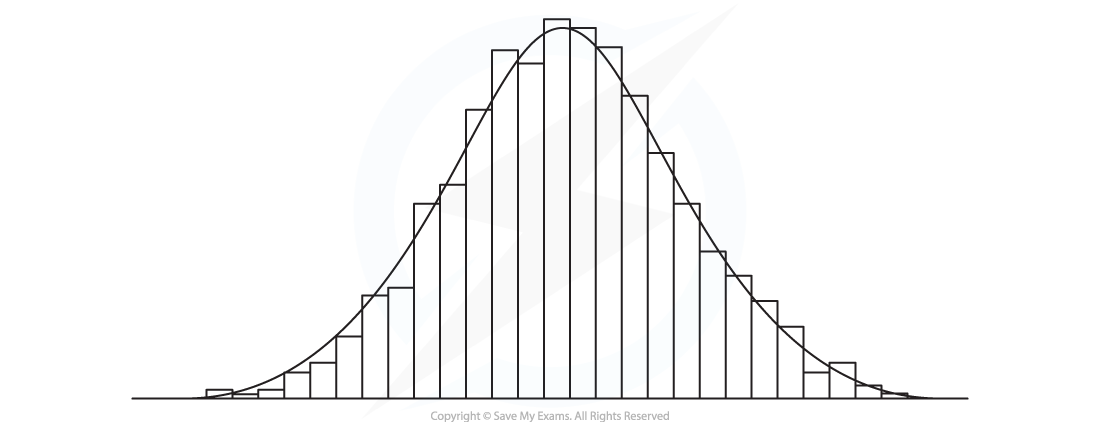
- A normal distribution can be used to model real-life data provided the histogram for this data is roughly symmetrical and bell-shaped
- If the variable is normally distributed then as more data is collected the outline of the histogram should get smoother and resemble a normal distribution curve
Can the binomial distribution and the normal distribution be used in the same question?
- Some questions might require you to first use the normal distribution to find the probability of success and then use the binomial distribution
- These questions normally involve some sort of sampling
- The key is to make sure you are very clear about what each parameter/variable represents
Worked Example
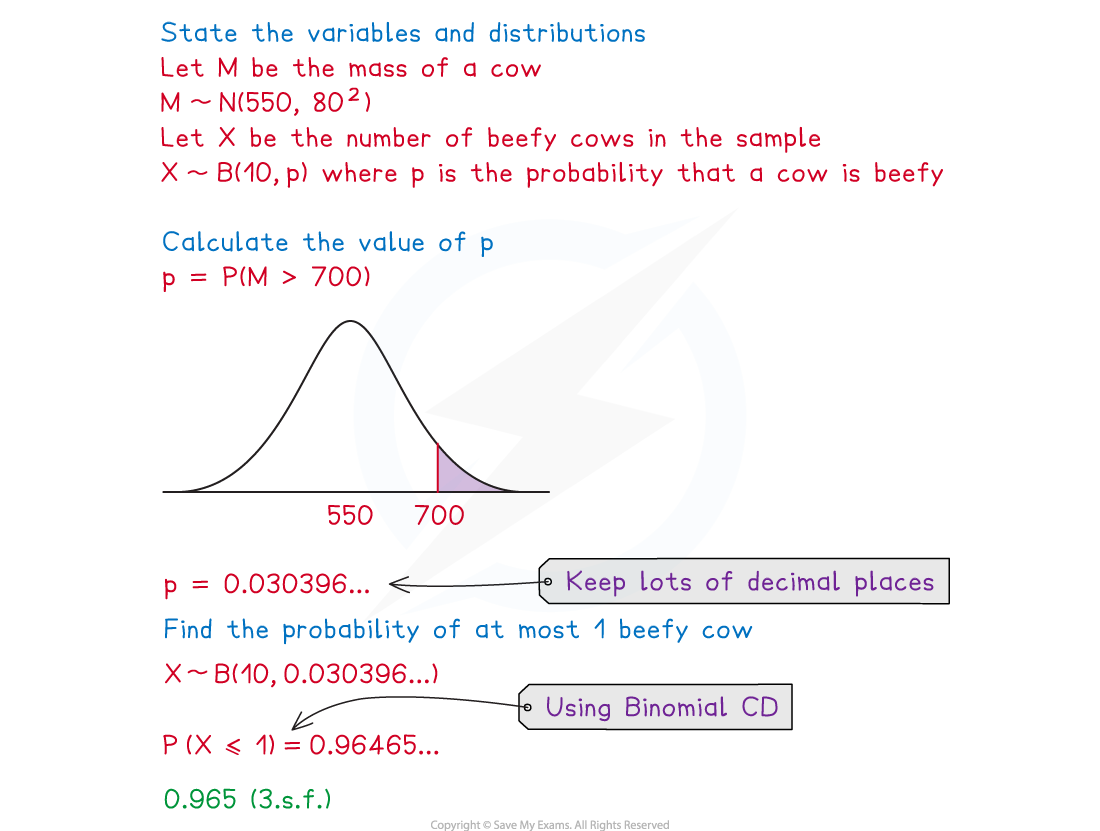
In a population of cows, the masses of the cows can be modelled using a normal distribution with mean 550 kg and standard deviation 80 kg. A farmer classifies cows as beefy if they weigh more than 700 kg. The farmer takes a random sample of 10 cows and weighs them.
Find the probability that at most one cow is beefy.
Exam Tip
- Always state what your variables and parameters represent. Make sure you know the conditions for when each distribution is (or is not) a suitable model.
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





