- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
AQA A Level Maths: Statistics复习笔记4.2.1 The Binomial Distribution
Properties of Binomial Distribution
What is a binomial distribution?
- A binomial distribution is a discrete probability distribution
- The discrete random variable follows a binomial distribution if it counts the number of successes when an experiment satisfies the conditions:
 What are the important properties of a binomial distribution?
What are the important properties of a binomial distribution?
 Square root to get the standard deviation
Square root to get the standard deviation
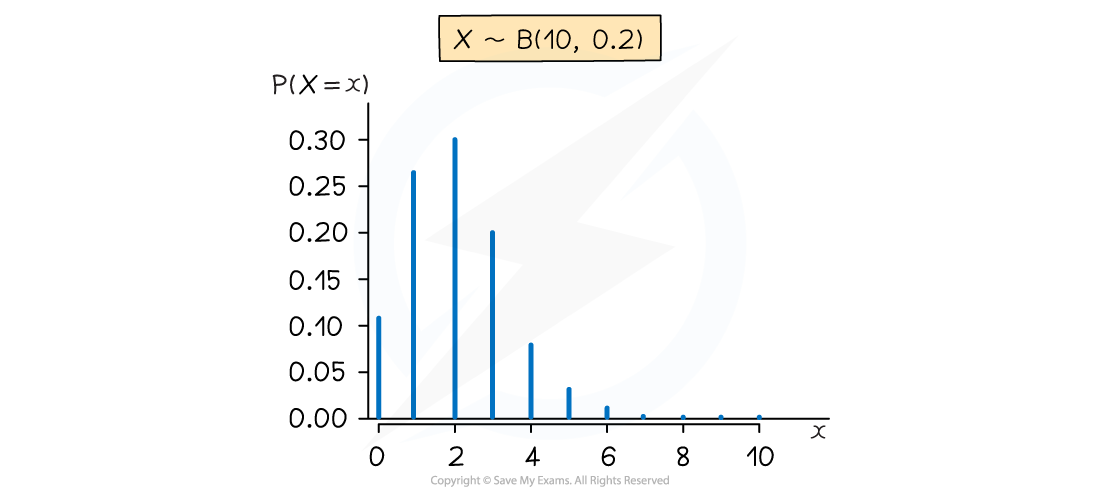
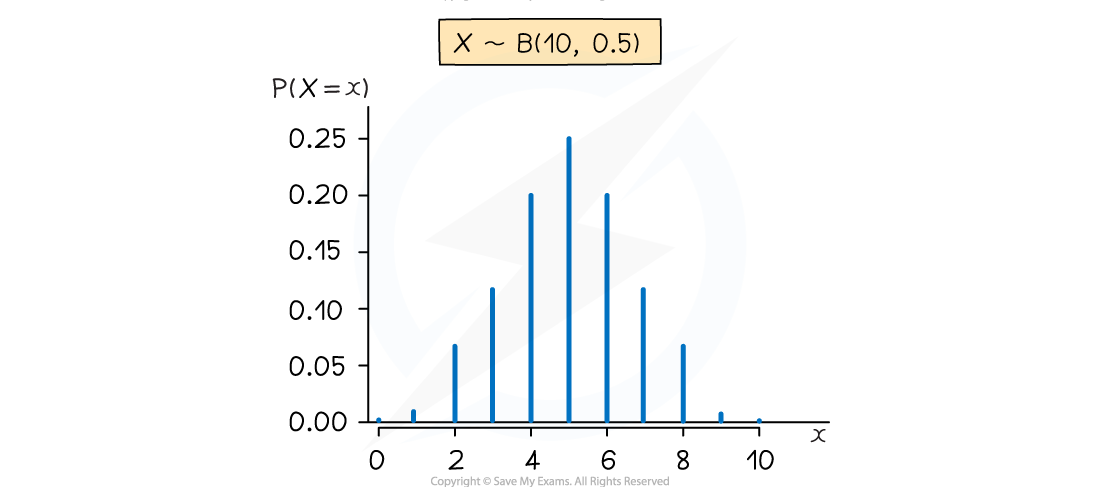
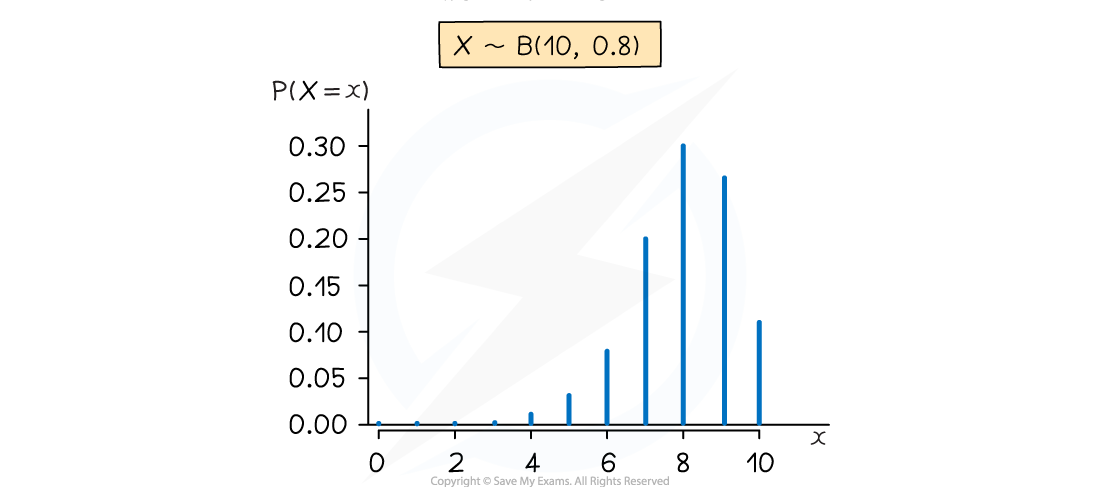
- The distribution can be represented visually using a vertical line graph
- If p is close to 0 then the graph has a tail to the right
- If p is close to 1 then the graph has a tail to the left
- If p is close to 0.5 then the graph is roughly symmetrical
- If p = 0.5 then the graph is symmetrical
Modelling with Binomial Distribution
How do I set up a binomial model?
- Identify what a trial is in the scenario
- For example: rolling a dice, flipping a coin, checking hair colour
- Identify what the successful outcome is in the scenario
- For example: rolling a 6, landing on tails, having black hair
- Make sure you clearly state what your random variable is
- For example, let X be the number of students in a class of 30 with black hair
What can be modelled using a binomial distribution?
- Anything that satisfies the four conditions
 As long as the population is large and the sample is random then it can be assumed that each person has a 30% chance of having blue eyes
As long as the population is large and the sample is random then it can be assumed that each person has a 30% chance of having blue eyes
What can not be modelled using a binomial distribution?
- Anything where the number of trials is not fixed or is infinite
- The number of emails received in an hour
- The number of times a coin is flipped until it lands on heads
- Anything where the outcome of one trial affects the outcome of the other trials
- The number of caramels that a person eats when they eat 5 sweets from a bag containing 6 caramels and 4 marshmallows
- If you eat a caramel for your first sweet then there are less caramels left in the bag when you choose your second sweet
- The number of caramels that a person eats when they eat 5 sweets from a bag containing 6 caramels and 4 marshmallows
- Anything where there are more than two outcomes of a trial
- A person's shoe size
- The number a dice lands on when rolled
- Anything where the probability of success changes
- The number of times that a person can swim a length of a swimming pool in under a minute when swimming 50 lengths
- The probability of swimming a lap in under a minute will decrease as the person gets tired
- The number of times that a person can swim a length of a swimming pool in under a minute when swimming 50 lengths
Worked Example
It is known that 8% of a large population are immune to a particular virus. Mark takes a sample of 50 people from this population. Mark uses a binomial model for the number of people in his sample that are immune to the virus
(a)State the distribution that Mark uses.
(b)State the two assumptions that Mark must make in order to use a binomial model.
(a)State the distribution that Mark uses.

(b)State the two assumptions that Mark must make in order to use a binomial model.

Exam Tip
- If you are asked to criticise a binomial model always consider whether the trials are independent, this is usually the one that stops a variable from following a binomial distribution!
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





