- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
AQA A Level Maths: Statistics复习笔记2.1.1 Basic Statistical Measures
Mean, Mode, Median
What are mean, median and mode?
- Mean, median and mode are measures of location
- A measure of location gives information about where data is in the number system
- Mean, median and mode are measures of central tendency
- They describe where the centre of the data is
- They are all types of averages
- In Statistics it is important to be specific about which average you are referring to
How are mean, median and mode calculated?
- You should already be familiar with finding the mean, median and mode from raw, ungrouped data
- The mode is the value that occurs most often in a data set
- In a frequency table the group or class that occurs most often will be referred to as the modal class
- A data set with more than one mode is bimodal
- The median is the middle value when the data is in order of size
- If there are two values in the middle of the data set, the median is the midpoint of the two values
- If finding median from a frequency table find the cumulative frequency first and find the group or class where the middle value will lie
- You may have to use linear interpolation when finding the median from a grouped frequency table
- The mean is the sum of all the values divided by the number of values in the data set
What are summary statistics and their notation? How do we choose the best measure of central tendency?
How do we choose the best measure of central tendency?
- It is often better to use one of the averages over the others, depending on the data set
- It’s a good idea to be aware of the advantages and disadvantages of the use of each average
- The mean uses all of the data values, this is good for a large data set where all of the values are close together, but also means that the mean can be affected by extreme values
- The median is not affected by very high or low values so is a good average to use in data sets with extreme values
- The mode is very useful in a lot of practical situations, however often there may be more than one mode, no mode or even a mode that is nowhere near the middle of the data set
Worked Example
For the data set given below, find the mode, median and mean.
23 19 14 28 27 19

Quartiles & Range
What are quartiles and percentiles?
- Quartiles and percentiles are measures of location
- Quartiles divide a population or data set into four equal sections
- The lower quartile, Q1, splits the lowest 25% from the highest 75%
- The median, Q2, is the value that is 50% of the way through the data
- The upper quartile, Q3, splits the lowest 75% from the highest 25%
- Percentiles divide the data into 100 parts
- The 70th percentile lies seven-tenths of the way through the data
- 70% of the data is below it and 30% is above it
- The 70th percentile lies seven-tenths of the way through the data
How are quartiles calculated? What are the range and interquartile range?
What are the range and interquartile range?
- The range and interquartile range are both measures of spread
- A measure of spread gives information about how spread out the data set is
- The range is the difference between the largest and smallest values in the data set
- All data points in the set will be included in the range, including extreme values
- The interquartile range is the difference between the upper quartile and the lower quartile
- Only the middle 50% of the data is included in the interquartile range
- It is not affected by extreme values
- Sometimes an interpercentile range could be asked for, this is the difference between two given percentiles
- For example, the 20th to 80th interpercentile range would be the difference between the 80th percentile and the 20th percentile
- The units for range and interquartile range are the same as the units for the original data
Worked Example
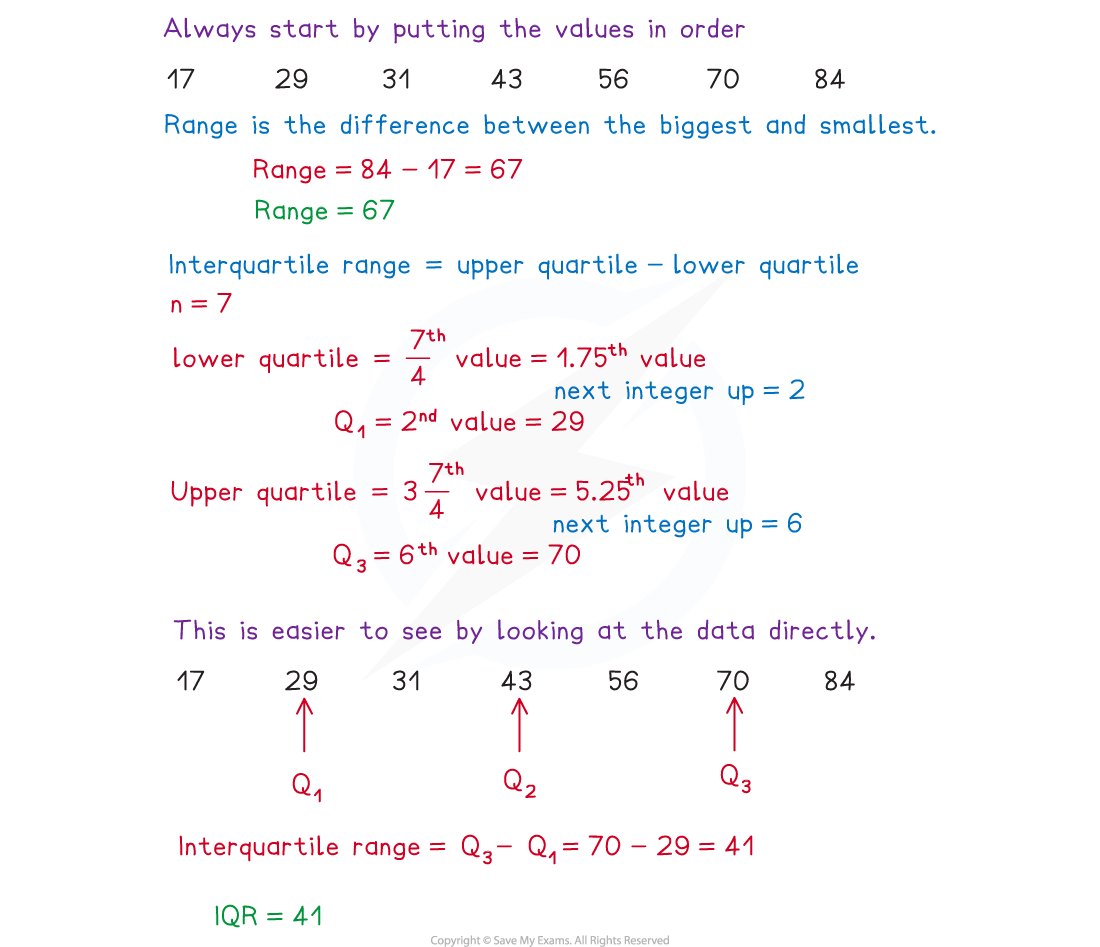
Find the range and interquartile range for the data set given below
43 29 70 31 84 56 17
Exam Tip
- Be aware of the difference between averages and ranges, especially when answering contextual questions asking you to describe or compare data. Remember, averages give an indication of where the data are whilst range gives an indication of how varied the data are.
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





