- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
AQA A Level Maths: Pure复习笔记10.1.4 Newton-Raphson
Newton-Raphson
The Newton-Raphson method
- The Newton-Raphson method finds roots of equations in the form f(x) = 0
- It can be used to find approximate solutions when an equation cannot be solved using the usual analytical methods
- It works by finding the x-intercept of tangents to f(x) to get closer and closer to a root
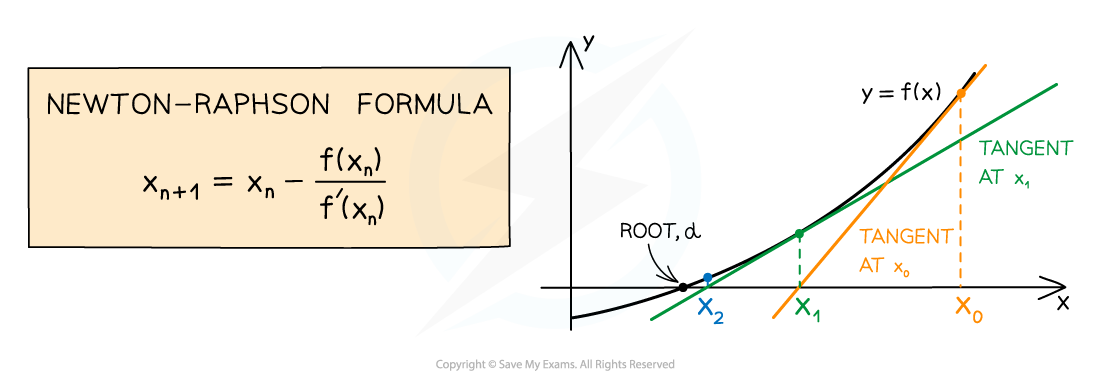
Using the Newton-Raphson method
- The formula for Newton-Raphson uses the same xn + 1 = f(xn) notation as used in iteration and other recurrence relations
- After using differentiation to find f’(x) the formula uses iteration to come to an ever more accurate solution
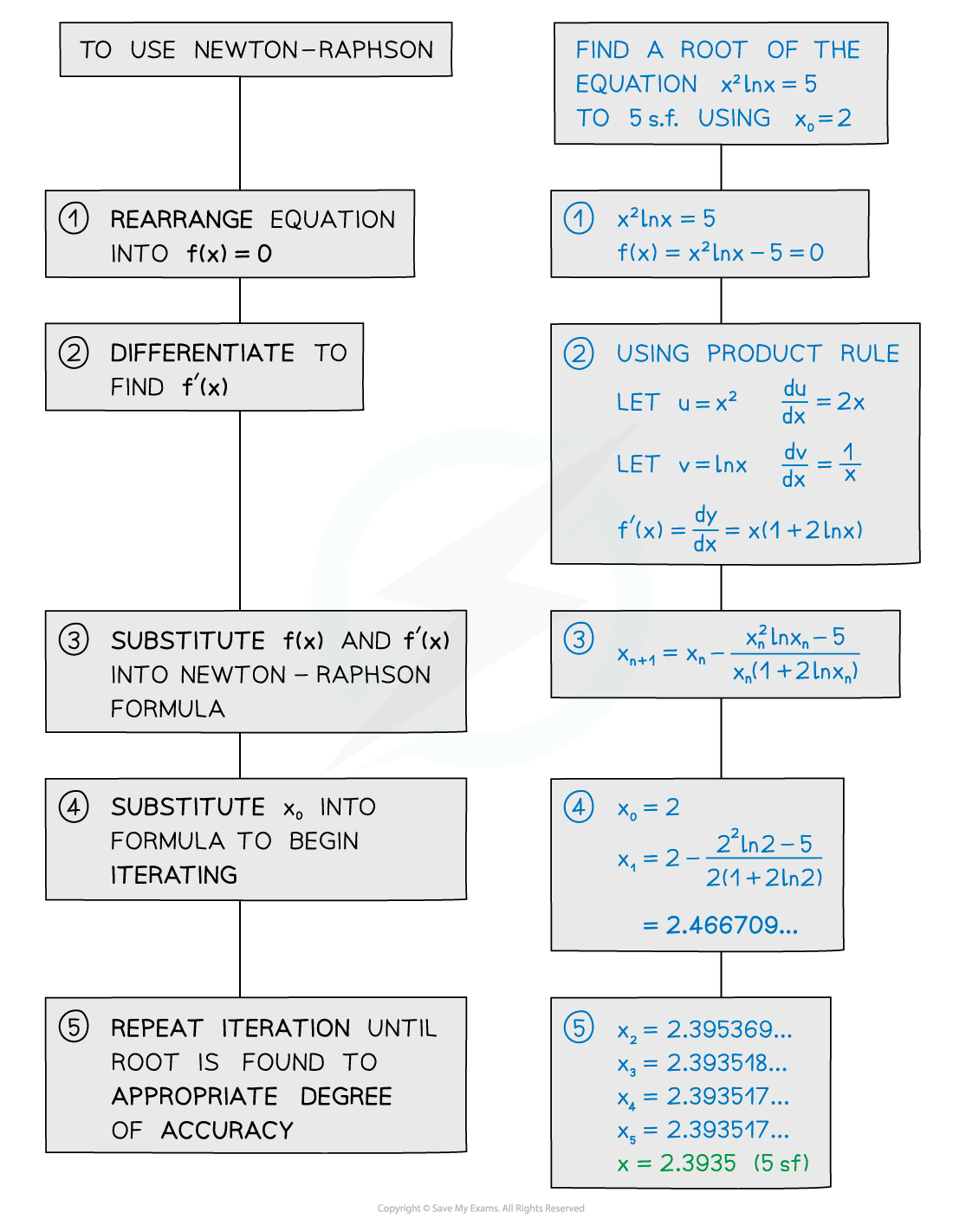
Can the Newton-Raphson method fail?
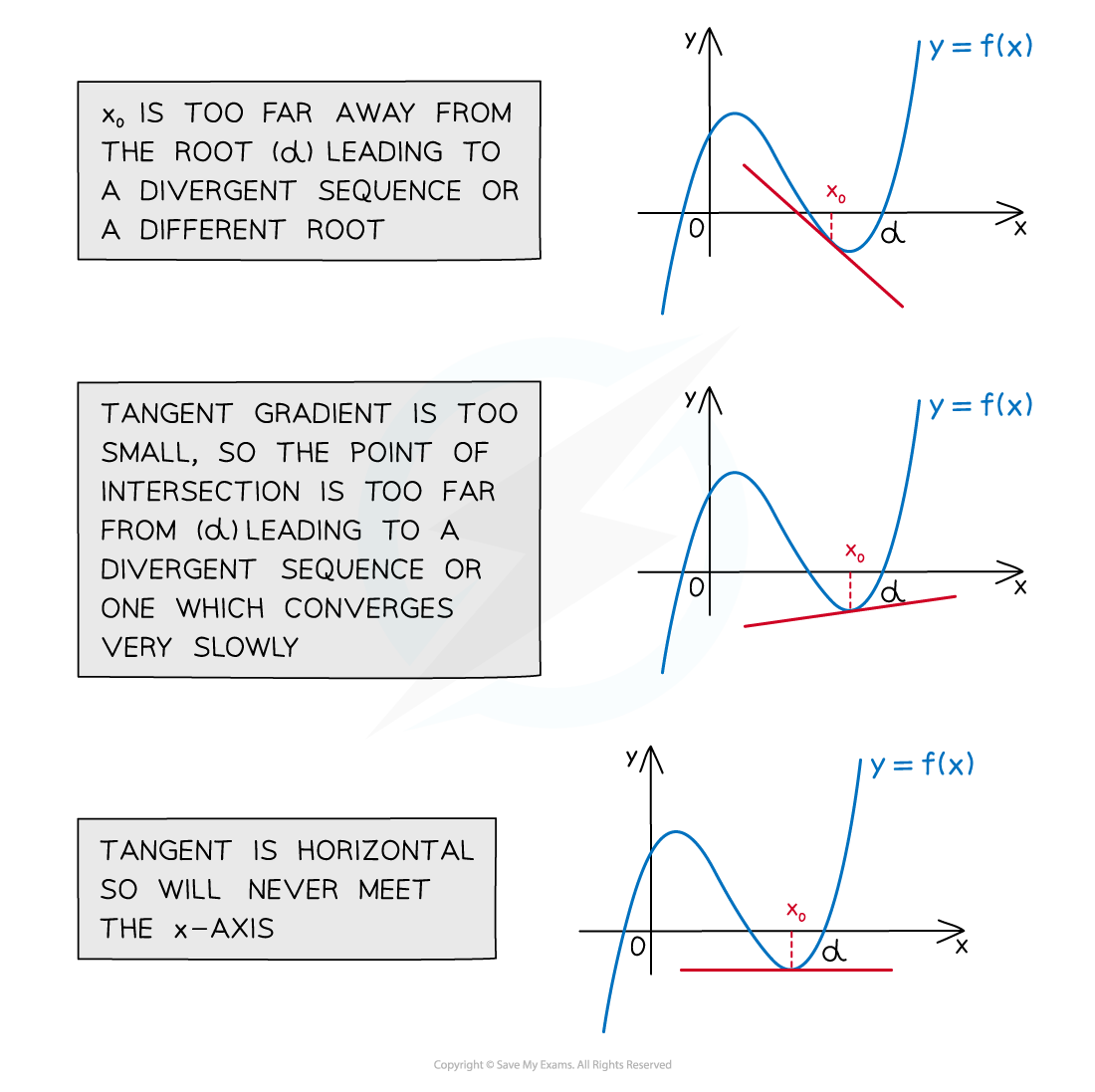
The Newton-Raphson method can fail when:
- the starting value x0 is too far away from the root leading to a divergent sequence or a different root
- the tangent gradient is too small, where f’(x) close to 0 leading to a divergent sequence or one which converges very slowly
- the tangent is horizontal, where f’(x) = 0 so the tangent will never meet the x‑axis
- the equation cannot be differentiated (or is awkward and time-consuming to do)
Exam Tip
- The formula for the Newton-Raphson method is given in the formula booklet.
- Use ANS button on your calculator to calculate repeated iterations.
- Keep track of your iterations using x2, x3… notation.
- Newton-Raphson questions may be part of bigger numerical methods questions.
Worked Example
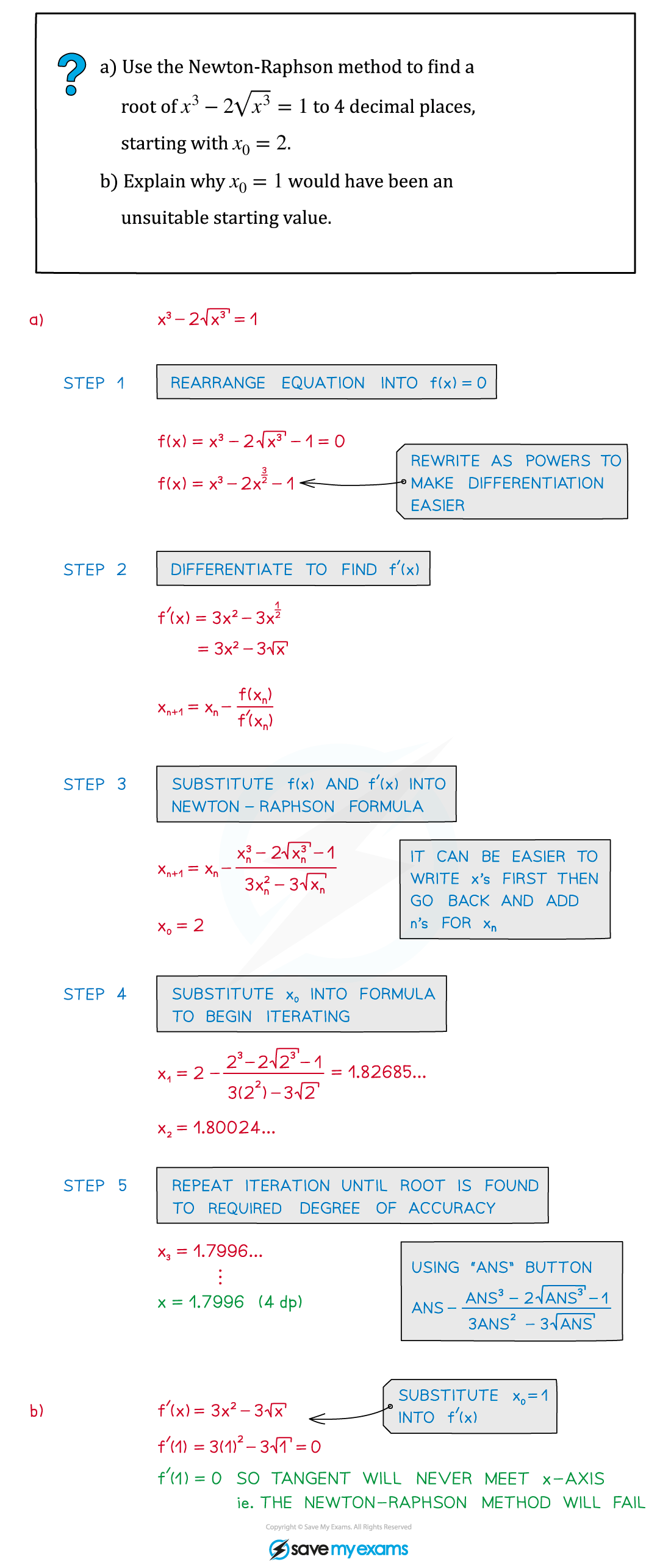
转载自savemyexams
站内搜索
竞赛真题免费下载(点击下载)
在线登记
最新发布
© 2024. All Rights Reserved. 沪ICP备2023009024号-1





